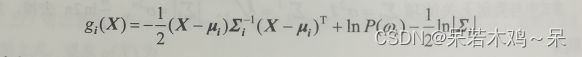基于最小错误率的贝叶斯决策(matlab实验)
数据集
I鸢尾花卉数据集包含150个数据样本,分为3类,每类50个数据,每个数据包含4个属性,其中可通过花萼长度,花萼宽度,花瓣长度,花瓣宽度4个属性预测鸢尾花卉属于(Setosa,Versicolour,Virginica)三个种类中的哪一类。
数据集下载链接:
链接:https://pan.baidu.com/s/1qlY4RVPOmRnKSRY9fVNzug
提取码:9ha5
最小错误率的贝叶斯决策
实验步骤
1、从Iris.txt文件中读取估计参数用的样本,每一类样本中抽出前40个分别求出均值:
>> iris = load('E:\persional\数据挖掘\iris.txt');
>> N =40;
%求第一类样本均值
>> for i=1:N
for j =1:4
w1(i,j) = iris(i,j);
end
end
>> sumx1 = sum(w1,1);
>> for i=1:4
meanx1(1,i) = sumx1(1,i)/N;
end
%求第二类样本均值
>>for i=1:N
for j=1:4
w2(i,j) = iris(i+50,j);
end
end
>> sumx2 = sum(w2,1);
>>for i=1:4
meanx2(1,i) = sumx2(1,i)/N;
end
%求第三类样本均值
>> for i=1:N
for j=1:4
w3(i,j) = iris(i+100,j);
end
end
>> sumx3 = sum(w3,1);
>> for i=1:4
meanx3(1,i)=sumx3(1,i)/N;
end
2、求每一类样本的协方差矩阵、逆矩阵及协方差矩阵的行列式:
%求样本第一类样本协方差矩阵
>> z1(4,4) = 0;
>> var1(4,4) = 0;
>> for i=1:4
for j=1:4
for k=1:N
z1(i,j) = z1(i,j)+(w1(k,i)-meanx1(1,i))*(w1(k,j)-meanx1(1,j));
end
var1(i,j)=z1(i,j)/(N-1);
end
end
%求样本第二类样本协方差矩阵
>> z2(4,4) = 0;
>> var2(4,4) = 0;
>> for i=1:4
for j=1:4
for k=1:N
z2(i,j) = z2(i,j)+(w2(k,i)-meanx2(1,i))*(w2(k,j)-meanx2(1,j));
end
var2(i,j)=z2(i,j)/(N-1);
end
end
%求样本第三类样本协方差矩阵
>> z3(4,4) = 0;
>> var3(4,4) = 0;
>> for i=1:4
for j=1:4
for k=1:N
z3(i,j) = z3(i,j)+(w3(k,i)-meanx3(1,i))*(w3(k,j)-meanx3(1,j));
end
var3(i,j)=z3(i,j)/(N-1);
end
end
%求各类的协方差矩阵逆矩阵及行列式
>> var1_inv = [];var1_det=[];
>> var2_inv = [];var2_det=[];
>> var3_inv = [];var3_det=[];
>> var1_inv=inv(var1);
>> var2_inv=inv(var2);
>> var3_inv=inv(var3);
>> var1_det = det(var1);
>> var2_det = det(var2);
>> var3_det = det(var3);
3、对三个类别,分别取每个组剩下的10个样本,每两组进行分类。由于每一类样本都相等,且每一类选取用作训练样本也相等,在每两组进行分类时,待分类样本的类先验概率P(w)=0.5,将各个样本代入判别函数,根据判别规则,gi(X)>gj(X),对于一切 j ≠ i成立,则X归为Wi类。
第一类后十个与第二类进行分类:
%第一类与第二类进行验证,取第一类数据的后十个来验证t2=0,t1=10
>> M = 10;
>> for i =1:M
for j=1:4
test(i,j) = iris(i+40,j);
end
end
>> p1 =0.5;
>> p2 = 0.5;
>> t1=0;t2=0;
>> for i=1:M
x=test(i,1);y=test(i,2);
z=test(i,3);h=test(i,4);
g1 = (-0.5)*([x,y,z,h]-meanx1)*var1_inv*([x,y,z,h]'-meanx1')-0.5*log(abs(var1_det))+log(p1);
g2 = (-0.5)*([x,y,z,h]-meanx2)*var2_inv*([x,y,z,h]'-meanx2')-0.5*log(abs(var2_det))+log(p2);
if g1>g2
t1 = t1+1
else
t2 = t2+1
end
end
第二类后十个样本与第三类进行分类:
%第二类与第三类进行验证,取第二类数据的后十个来验证t2=10,t3=0
>> M = 10;
>> for i =1:M
for j=1:4
test(i,j) = iris(i+90,j);
end
end
>> p2 = 0.5;
>> p3 = 0.5;
>> t2=0;t3=0;
>> for i=1:M
x=test(i,1);y=test(i,2);
z=test(i,3);h=test(i,4);
g2 = (-0.5)*([x,y,z,h]-meanx2)*var2_inv*([x,y,z,h]'-meanx2')-0.5*log(abs(var2_det))+log(p2);
g3 = (-0.5)*([x,y,z,h]-meanx3)*var3_inv*([x,y,z,h]'-meanx3')-0.5*log(abs(var3_det))+log(p3);
if g2>g3
t2=t2+1;
else
t3 =t3+1;
end
end
第三类后十个样本与第一类进行分类:
%第一类与第三类进行验证,取第三类数据的后十个来验证t2=10,t3=0
>> M = 10;
>> for i =1:M
for j=1:4
test(i,j) = iris(i+140,j);
end
end
>> p1 = 0.5;
>> p3 = 0.5;
>> t1=0;t3=0;
>> for i=1:M
x=test(i,1);y=test(i,2);
z=test(i,3);h=test(i,4);
g1 = (-0.5)*([x,y,z,h]-meanx1)*var1_inv*([x,y,z,h]'-meanx1')-0.5*log(abs(var1_det))+log(p1);
g3 = (-0.5)*([x,y,z,h]-meanx3)*var3_inv*([x,y,z,h]'-meanx3')-0.5*log(abs(var3_det))+log(p3);
if g1>g3
t1=t1+1;
else
t3 =t3+1;
end
end
实验结果及分析
1、取第一类样本后十个数据,进行W1和W2进行分类:t1 = 10,t2=0,分类正确;
2、取第二类样本后十个数据,进行W2和W3进行分类:t2 = 10,t3=0,分类正确;
3、取第三类样本后十个数据,进行W3和W1进行分类:t3 = 10,t1=0,分类正确;
求样本类的均值:
>> a1 = [meanx1(1,1);meanx2(1,1);meanx3(1,1)]
a1 =
5.0375
6.0100
6.3000
>> b2 = [meanx1(1,2);meanx2(1,2);meanx3(1,2)]
b2 =
3.4400
2.7800
3.3000
>> c3 = [meanx1(1,3);meanx2(1,3);meanx3(1,3)]
c3 =
1.4625
4.3175
6.0000
>> d4 = [meanx1(1,4);meanx2(1,4);meanx3(1,4)]
d4 =
0.2325
1.3500
2.5000
>> Name = {'w1','w2','w3'};
>> table(a1,b2,c3,d4,'VariableNames',{'x1','x2','x3','x4'},'RowNames',Name);
由图可知,对于样本W1,W2,W3,其中第二个特征的均值相差不大,不如其他三个特征,因此忽略第二个特征,在三维坐标空间中画出三类样本点的空间分布:
>> iris = load('E:\persional\数据挖掘\iris.txt');
>> data = iris;
>> data(:,2,:,:)=[];
>> N =50;
%求第一类样本均值
>> for i=1:N
for j =1:3
w1(i,j) = data(i,j);
end
end
>> sumx1 = sum(w1,1);
>> for i=1:3
meanx1(1,i) = sumx1(1,i)/N;
end
%求第二类样本均值
>> for i=1:N
for j=1:3
w2(i,j) = data(i+50,j);
end
end
>> sumx2 = sum(w2,1);
>> for i=1:3
meanx2(1,i) = sumx2(1,i)/N;
end
%求第三类样本均值
>> for i=1:N
for j=1:3
w3(i,j) = data(i+100,j);
end
end
>> sumx3 = sum(w3,1);
>> for i=1:3
meanx3(1,i)=sumx3(1,i)/N;
end
>> %求样本第一类样本协方差矩阵
>> z1(3,3) = 0;
>> var1(3,3) = 0;
>> for i=1:3
for j=1:3
for k=1:N
z1(i,j) = z1(i,j)+(w1(k,i)-meanx1(1,i))*(w1(k,j)-meanx1(1,j));
end
var1(i,j)=z1(i,j)/(N-1);
end
end
%求样本第二类样本协方差矩阵
>> z2(3,3) = 0;
>> var2(3,3) = 0;
>> for i=1:3
for j=1:3
for k=1:N
z2(i,j) = z2(i,j)+(w2(k,i)-meanx2(1,i))*(w2(k,j)-meanx2(1,j));
end
var2(i,j)=z2(i,j)/(N-1);
end
end
%求样本第三类样本协方差矩阵
>> z3(3,3) = 0;
>> var3(3,3) = 0;
>> for i=1:3
for j=1:3
for k=1:N
z3(i,j) = z3(i,j)+(w3(k,i)-meanx3(1,i))*(w3(k,j)-meanx3(1,j));
end
var3(i,j)=z3(i,j)/(N-1);
end
end
%求各类的协方差矩阵逆矩阵及行列式
>> var1_inv = [];var1_det=[];
>> var2_inv = [];var2_det=[];
>> var3_inv = [];var3_det=[];
>> var1_inv=inv(var1);
>> var2_inv=inv(var2);
>> var3_inv=inv(var3);
>> var1_det = det(var1);
>> var2_det = det(var2);
>> var3_det = det(var3);
>>[H,W] = size(iris);
>> p1=0.5;p2=0.5;p3=0.5;
>> t1=0;t2=0;t3=0;
>> for i =1:H
x = data(i,1);y =data(i,2);z = data(i,3);
g1 = (-0.5)*([x,y,z]-meanx1)*var1_inv*([x,y,z]-meanx1)'-0.5*log(abs(var1_det))+log(p1);
g2 = (-0.5)*([x,y,z]-meanx2)*var2_inv*([x,y,z]-meanx2)'-0.5*log(abs(var2_det))+log(p2);
g3 = (-0.5)*([x,y,z]-meanx3)*var3_inv*([x,y,z]-meanx3)'-0.5*log(abs(var3_det))+log(p3);
g = [g1 g2 g3];
gmax = max(g);
if gmax == g1
plot3(x,y,z,'b*');grid on;hold on;
elseif gmax == g2
plot3(x,y,z,'r+');grid on;hold on;
elseif gmax ==g3
plot3(x,y,z,'g>');grid on;hold on;
end
end
由图可得:蓝色为第一类,红色为第二类,绿色为第三类,明显第一类与第二、三类的差异很大,而第二类与第三类的差别较小,对于位于第二、三类附近的样本,使用最小错误率贝叶斯决策时,可能会有出错的概率。