深度学习 第3章线性分类 实验四 pytorch实现 Softmax回归 鸢尾花分类任务 下篇

第3章 线性分类

这篇内容是实践，会调用一些函数，代码已经在最后展出，可以直接用

3.3 实践：基于Softmax回归完成鸢尾花分类任务

在本节，我们用入门深度学习的基础实验之一“鸢尾花分类任务”来进行实践，使用经典学术数据集Iris作为训练数据，实现基于Softmax回归的鸢尾花分类任务。

实践流程主要包括以下7个步骤：数据处理、模型构建、损失函数定义、优化器构建、模型训练、模型评价和模型预测等，

• 数据处理：根据网络接收的数据格式，完成相应的预处理操作，保证模型正常读取；
• 模型构建：定义Softmax回归模型类；
• 训练配置：训练相关的一些配置，如：优化算法、评价指标等；
• 组装Runner类：Runner用于管理模型训练和测试过程；
• 模型训练和测试：利用Runner进行模型训练、评价和测试。

本实践的主要配置如下：

• 数据：Iris数据集；
• 模型：Softmax回归模型；
• 损失函数：交叉熵损失；
• 优化器：梯度下降法；
• 评价指标：准确率。

3.3.1 数据处理

3.3.1.1 数据集介绍

Iris数据集，也称为鸢尾花数据集，包含了3种鸢尾花类别（Setosa、Versicolour、Virginica），每种类别有50个样本，共计150个样本。其中每个样本中包含了4个属性：花萼长度、花萼宽度、花瓣长度以及花瓣宽度，本实验通过鸢尾花这4个属性来判断该样本的类别。

鸢尾花属性

属性1	属性2	属性3	属性4
sepal_length	sepal_width	petal_length	petal_width
花萼长度	花萼宽度	花瓣长度	花瓣宽度

鸢尾花类别

英文名	中文名	标签
Setosa	Iris	狗尾草鸢尾
Versicolour	Iris	杂色鸢尾
Virginica	Iris	弗吉尼亚鸢尾

鸢尾花属性类别对应预览

sepal_length	sepal_width	petal_length	petal_width	species
5.1	3.5	1.4	0.2	setosa
4.9	3	1.4	0.2	setosa
4.7	3.2	1.3	0.2	setosa
…	…	…	…	…

3.3.1.2 数据清洗

1. 缺失值分析

对数据集中的缺失值或异常值等情况进行分析和处理，保证数据可以被模型正常读取。

代码实现如下：

from sklearn.datasets import load_iris
import pandas
import numpy as np

# 对数据集中的缺失值或异常值等情况进行分析和处理，保证数据可以被模型正常读取。代码实现如下：
iris_features = np.array(load_iris().data, dtype=np.float32)
iris_labels = np.array(load_iris().target, dtype=np.int32)
print(pandas.isna(iris_features).sum())
print(pandas.isna(iris_labels).sum())

运行结果：

0
0

从输出结果看，鸢尾花数据集中不存在缺失值的情况。

2. 异常值处理

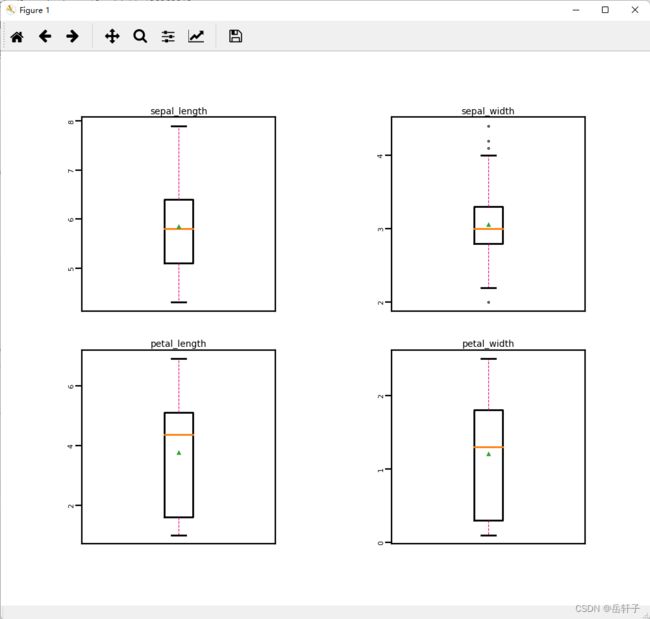
通过箱线图直观的显示数据分布，并观测数据中的异常值。

# 通过箱线图直观的显示数据分布，并观测数据中的异常值。
import matplotlib.pyplot as plt #可视化工具

# 箱线图查看异常值分布
def boxplot(features):
    feature_names = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width']

    # 连续画几个图片
    plt.figure(figsize=(5, 5), dpi=200)
    # 子图调整
    plt.subplots_adjust(wspace=0.6)
    # 每个特征画一个箱线图
    for i in range(4):
        plt.subplot(2, 2, i+1)
        # 画箱线图
        plt.boxplot(features[:, i], 
                    showmeans=True, 
                    whiskerprops={"color":"#E20079", "linewidth":0.4, 'linestyle':"--"},
                    flierprops={"markersize":0.4},
                    meanprops={"markersize":1})
        # 图名
        plt.title(feature_names[i], fontdict={"size":5}, pad=2)
        # y方向刻度
        plt.yticks(fontsize=4, rotation=90)
        plt.tick_params(pad=0.5)
        # x方向刻度
        plt.xticks([])
    plt.savefig('ml-vis.pdf')
    plt.show()

boxplot(iris_features)

运行结果：

从输出结果看，数据中基本不存在异常值，所以不需要进行异常值处理。

3.3.1.3 数据读取

本实验中将数据集划分为了三个部分：

• 训练集：用于确定模型参数；
• 验证集：与训练集独立的样本集合，用于使用提前停止策略选择最优模型；
• 测试集：用于估计应用效果（没有在模型中应用过的数据，更贴近模型在真实场景应用的效果）。

在本实验中，将$80\%$的数据用于模型训练，$10\%$的数据用于模型验证，$10\%$的数据用于模型测试。

代码实现如下：

# 加载数据集
def load_data(shuffle=True):
    '''
    加载鸢尾花数据
    输入：
        - shuffle：是否打乱数据，数据类型为bool
    输出：
        - X：特征数据，shape=[150,4]
        - y：标签数据, shape=[150]
    '''
    # 加载原始数据
    X = np.array(load_iris().data, dtype=np.float32)
    y = np.array(load_iris().target, dtype=np.float32)

    X = torch.tensor(X)
    y = torch.tensor(y)

    # 数据归一化
    X_min = torch.min(X, dim=0).values
    X_max = torch.max(X, dim=0).values
    X = (X-X_min) / (X_max-X_min)

    # 如果shuffle为True,随机打乱数据
    if shuffle:
        idx = torch.randperm(X.shape[0])
        X = X[idx]
        y = y[idx]
    return X, y

# 固定随机种子
torch.manual_seed(102)

num_train = 120
num_dev = 15
num_test = 15

X, y = load_data(shuffle=True)
print("X shape: ", X.shape, "y shape: ", y.shape)
X_train, y_train = X[:num_train], y[:num_train]
X_dev, y_dev = X[num_train:num_train + num_dev], y[num_train:num_train + num_dev]
X_test, y_test = X[num_train + num_dev:], y[num_train + num_dev:]

运行结果：

X shape:  torch.Size([150, 4]) y shape:  torch.Size([150])

# 打印X_train和y_train的维度
print("X_train shape: ", X_train.shape, "y_train shape: ", y_train.shape)

运行结果：

X_train shape:  torch.Size([120, 4]) y_train shape:  torch.Size([120])

# 打印前5个数据的标签
print(y_train[:5])

运行结果：

tensor([1., 2., 0., 1., 2.])

3.3.2 模型构建

使用Softmax回归模型进行鸢尾花分类实验，将模型的输入维度定义为4，输出维度定义为3。

代码实现如下：

import op

# 输入维度
input_dim = 4
# 类别数
output_dim = 3
# 实例化模型
model = op.model_SR(input_dim=input_dim, output_dim=output_dim)

3.3.3 模型训练

实例化RunnerV2类，使用训练集和验证集进行模型训练，共训练80个epoch，其中每隔10个epoch打印训练集上的指标，并且保存准确率最高的模型作为最佳模型。

代码实现如下：

import op, metric, opitimizer, RunnerV2

# 学习率
lr = 0.2

# 梯度下降法
optimizer = opitimizer.SimpleBatchGD(init_lr=lr, model=model)
# 交叉熵损失
loss_fn = op.MultiCrossEntropyLoss()
# 准确率
metric2 = metric.accuracy

# 实例化RunnerV2
runner = RunnerV2.RunnerV2(model, optimizer, metric2, loss_fn)

# # 启动训练
runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=200, log_epochs=10, save_path="best_model.pdparams")

运行结果：

best accuracy performence has been updated: 0.00000 --> 0.46667
[Train] epoch: 0, loss: 1.09861159324646, score: 0.375
[Dev] epoch: 0, loss: 1.0893398523330688, score: 0.46666666865348816
[Train] epoch: 10, loss: 0.9781171679496765, score: 0.699999988079071
[Dev] epoch: 10, loss: 1.0236393213272095, score: 0.46666666865348816
[Train] epoch: 20, loss: 0.8900946974754333, score: 0.699999988079071
[Dev] epoch: 20, loss: 0.9741119742393494, score: 0.46666666865348816
[Train] epoch: 30, loss: 0.8204634189605713, score: 0.699999988079071
[Dev] epoch: 30, loss: 0.9319687485694885, score: 0.46666666865348816
[Train] epoch: 40, loss: 0.76439368724823, score: 0.699999988079071
[Dev] epoch: 40, loss: 0.896036684513092, score: 0.46666666865348816
[Train] epoch: 50, loss: 0.7185509204864502, score: 0.7250000238418579
[Dev] epoch: 50, loss: 0.8653663396835327, score: 0.46666666865348816
[Train] epoch: 60, loss: 0.6804777979850769, score: 0.7416666746139526
[Dev] epoch: 60, loss: 0.8390589952468872, score: 0.46666666865348816
[Train] epoch: 70, loss: 0.6483750939369202, score: 0.7583333253860474
[Dev] epoch: 70, loss: 0.816339910030365, score: 0.46666666865348816
[Train] epoch: 80, loss: 0.6209224462509155, score: 0.7666666507720947
[Dev] epoch: 80, loss: 0.796570360660553, score: 0.46666666865348816
[Train] epoch: 90, loss: 0.5971452593803406, score: 0.7833333611488342
[Dev] epoch: 90, loss: 0.7792339324951172, score: 0.46666666865348816
[Train] epoch: 100, loss: 0.5763141512870789, score: 0.8166666626930237
[Dev] epoch: 100, loss: 0.7639160752296448, score: 0.46666666865348816
best accuracy performence has been updated: 0.46667 --> 0.53333
[Train] epoch: 110, loss: 0.5578767657279968, score: 0.824999988079071
[Dev] epoch: 110, loss: 0.7502836585044861, score: 0.5333333611488342
best accuracy performence has been updated: 0.53333 --> 0.60000
[Train] epoch: 120, loss: 0.5414095520973206, score: 0.824999988079071
[Dev] epoch: 120, loss: 0.7380689382553101, score: 0.6000000238418579
[Train] epoch: 130, loss: 0.5265832543373108, score: 0.8500000238418579
[Dev] epoch: 130, loss: 0.7270554304122925, score: 0.6000000238418579
[Train] epoch: 140, loss: 0.5131379961967468, score: 0.8500000238418579
[Dev] epoch: 140, loss: 0.7170670628547668, score: 0.6000000238418579
[Train] epoch: 150, loss: 0.5008670687675476, score: 0.875
[Dev] epoch: 150, loss: 0.707959771156311, score: 0.6000000238418579
best accuracy performence has been updated: 0.60000 --> 0.66667
[Train] epoch: 160, loss: 0.48960402607917786, score: 0.875
[Dev] epoch: 160, loss: 0.6996145844459534, score: 0.6666666865348816
[Train] epoch: 170, loss: 0.4792129397392273, score: 0.875
[Dev] epoch: 170, loss: 0.6919329166412354, score: 0.6666666865348816
[Train] epoch: 180, loss: 0.46958208084106445, score: 0.875
[Dev] epoch: 180, loss: 0.6848322749137878, score: 0.6000000238418579
[Train] epoch: 190, loss: 0.46061864495277405, score: 0.875
[Dev] epoch: 190, loss: 0.6782433390617371, score: 0.6000000238418579

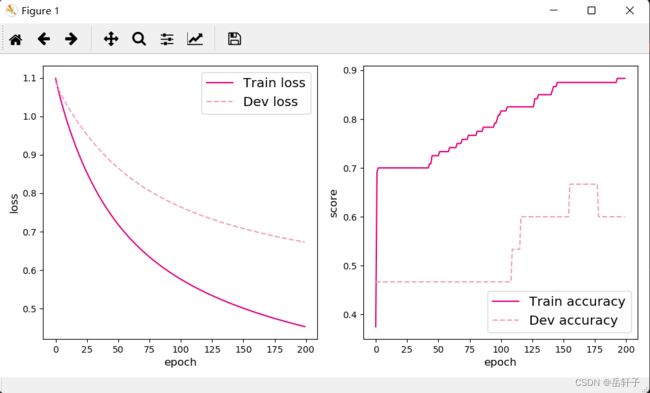
可视化观察训练集与验证集的准确率变化情况。

import plot

plot.plot(runner,fig_name='linear-acc3.pdf')

运行结果：

3.3.4 模型评价

使用测试数据对在训练过程中保存的最佳模型进行评价，观察模型在测试集上的准确率情况。

代码实现如下：

# 加载最优模型
runner.load_model('best_model.pdparams')
# 模型评价
score, loss = runner.evaluate([X_test, y_test])
print("[Test] score/loss: {:.4f}/{:.4f}".format(score, loss))

运行结果：

[Test] score/loss: 0.7333/0.5930

3.3.5 模型预测

使用保存好的模型，对测试集中的数据进行模型预测，并取出1条数据观察模型效果。

代码实现如下：

# 预测测试集数据
logits = runner.predict(X_test)
# 观察其中一条样本的预测结果
pred = torch.argmax(logits[0]).numpy()
print("pred:",pred)
# 获取该样本概率最大的类别
label = y_test[0].numpy()
print("label:",label)
# 输出真实类别与预测类别
print("The true category is {0} and the predicted category is {1}".format(label, pred))

运行结果：

pred: 2
label: 2.0
The true category is 2.0 and the predicted category is 2

---

下篇需要的包

1. op.py

import torch
import os
from activation import softmax
os.environ["KMP_DUPLICATE_LIB_OK"]="TRUE" # 这里报错
torch.manual_seed(10) #设置随机种子

class Op(object):
    def __init__(self):
        pass

    def __call__(self, inputs):
        return self.forward(inputs)

    def forward(self, inputs):
        raise NotImplementedError

    def backward(self, inputs):
        raise NotImplementedError

# 线性算子
class Linear(Op):
    def __init__(self,input_size):
        """
        输入：
           - input_size:模型要处理的数据特征向量长度
        """

        self.input_size = input_size

        # 模型参数
        self.params = {}
        self.params['w'] = torch.randn(size=[self.input_size,1],dtype=torch.float32) 
        self.params['b'] = torch.zeros(size=[1],dtype=torch.float32)

    def __call__(self, X):
        return self.forward(X)

    # 前向函数
    def forward(self, X):
        """
        输入：
           - X: tensor, shape=[N,D]
           注意这里的X矩阵是由N个x向量的转置拼接成的，与原教材行向量表示方式不一致
        输出：
           - y_pred： tensor, shape=[N]
        """

        N,D = X.shape

        if self.input_size==0:
            return torch.full(size=[N,1], fill_value=self.params['b'])
        
        assert D==self.input_size # 输入数据维度合法性验证

        # 使用torch.matmul计算两个tensor的乘积
        y_pred = torch.matmul(X,self.params['w'])+self.params['b']
        
        return y_pred

#新增Softmax算子
class model_SR(Op):
    def __init__(self, input_dim, output_dim):
        super(model_SR, self).__init__()
        self.params = {}
        # 将线性层的权重参数全部初始化为0
        self.params['W'] = torch.zeros(size=[input_dim, output_dim])
        # self.params['W'] = paddle.normal(mean=0, std=0.01, shape=[input_dim, output_dim])
        # 将线性层的偏置参数初始化为0
        self.params['b'] = torch.zeros(size=[output_dim])
        # 存放参数的梯度
        self.grads = {}
        self.X = None
        self.outputs = None
        self.output_dim = output_dim

    def __call__(self, inputs):
        return self.forward(inputs)

    def forward(self, inputs):
        self.X = inputs
        # 线性算子
        score = torch.matmul(self.X, self.params['W']) + self.params['b']
        # Softmax函数
        self.outputs = softmax(score)
        return self.outputs

    def backward(self, labels):
        """
        输入：
            - labels：真实标签，shape=[N, 1]，其中N为样本数量
        """
        # 计算偏导数
        N =labels.shape[0]
        labels = torch.nn.functional.one_hot(labels.to(torch.int64), self.output_dim)
        self.grads['W'] = -1 / N * torch.matmul(self.X.t(), (labels-self.outputs))
        self.grads['b'] = -1 / N * torch.matmul(torch.ones(size=[N]), (labels-self.outputs))

#新增多类别交叉熵损失
class MultiCrossEntropyLoss(Op):
    def __init__(self):
        self.predicts = None
        self.labels = None
        self.num = None
    
    def __call__(self, predicts, labels):
        return self.forward(predicts, labels)

    def forward(self, predicts, labels):
        """
        输入：
            - predicts：预测值，shape=[N, 1]，N为样本数量
            - labels：真实标签，shape=[N, 1]
        输出：
            - 损失值：shape=[1]
        """
        self.predicts = predicts
        self.labels = labels
        self.num = self.predicts.shape[0]
        loss = 0
        for i in range(0, self.num):
            index = self.labels[i].int()
            loss -= torch.log(self.predicts[i][index])
        return loss / self.num

2. opitimizer.py

import torch
from abc import abstractmethod

def optimizer_lsm(model, X, y, reg_lambda=0):
  """
    输入：
       - model: 模型
       - X: tensor, 特征数据，shape=[N,D]
       - y: tensor,标签数据，shape=[N]
       - reg_lambda: float, 正则化系数，默认为0
    输出：
       - model: 优化好的模型
    """

  N, D = X.shape

  # 对输入特征数据所有特征向量求平均
  x_bar_tran = torch.mean(X,dim=0).t()
  
  # 求标签的均值,shape=[1]
  y_bar = torch.mean(y)
  
  # torch.subtract通过广播的方式实现矩阵减向量
  x_sub = torch.subtract(X,x_bar_tran)

  # 使用torch.all判断输入tensor是否全0
  if torch.all(x_sub==0):
    model.params['b'] = y_bar
    model.params['w'] = torch.zeros(size=[D])
    return model
  
  # torch.inverse求方阵的逆
  tmp = torch.inverse(torch.matmul(x_sub.T,x_sub)+
          reg_lambda*torch.eye(n = (D)))

  w = torch.matmul(torch.matmul(tmp,x_sub.T),(y-y_bar))
  
  b = y_bar-torch.matmul(x_bar_tran,w)
  
  model.params['b'] = b
  model.params['w'] = torch.squeeze(w,dim=-1)

  return model

#新增优化器基类
class Optimizer(object):
    def __init__(self, init_lr, model):
        """
        优化器类初始化
        """
        #初始化学习率，用于参数更新的计算
        self.init_lr = init_lr
        #指定优化器需要优化的模型
        self.model = model

    @abstractmethod
    def step(self):
        """
        定义每次迭代如何更新参数
        """
        pass


#新增梯度下降法优化器
class SimpleBatchGD(Optimizer):
    def __init__(self, init_lr, model):
        super(SimpleBatchGD, self).__init__(init_lr=init_lr, model=model)

    def step(self):
        #参数更新
        #遍历所有参数，按照公式(3.8)和(3.9)更新参数
        if isinstance(self.model.params, dict):
            for key in self.model.params.keys():
                self.model.params[key] = self.model.params[key] - self.init_lr * self.model.grads[key]

3. metric.py

import torch

def accuracy(preds, labels):
    """
    输入：
        - preds：预测值，二分类时，shape=[N, 1]，N为样本数量，多分类时，shape=[N, C]，C为类别数量
        - labels：真实标签，shape=[N, 1]
    输出：
        - 准确率：shape=[1]
    """
    # 判断是二分类任务还是多分类任务，preds.shape[1]=1时为二分类任务，preds.shape[1]>1时为多分类任务
    if preds.shape[1] == 1:
        # 二分类时，判断每个概率值是否大于0.5，当大于0.5时，类别为1，否则类别为0
        # 使用'torch.tensor()'将preds的数据类型转换为float32类型
        preds = torch.as_tensor((preds >= 0.5),dtype=torch.float32)
    else:
        # 多分类时，使用'torch.argmax'计算最大元素索引作为类别
        preds = torch.argmax(preds, dim=1).int()
    return torch.mean(torch.as_tensor((preds == labels),dtype=torch.float32))

4. RunnerV2.py

import torch

#新增RunnerV2类
class RunnerV2(object):
    def __init__(self, model, optimizer, metric, loss_fn):
        self.model = model
        self.optimizer = optimizer
        self.loss_fn = loss_fn
        self.metric = metric
        #记录训练过程中的评价指标变化情况
        self.train_scores = []
        self.dev_scores = []
        #记录训练过程中的损失函数变化情况
        self.train_loss = []
        self.dev_loss = []

    def train(self, train_set, dev_set, **kwargs):
        #传入训练轮数，如果没有传入值则默认为0
        num_epochs = kwargs.get("num_epochs", 0)
        #传入log打印频率，如果没有传入值则默认为100
        log_epochs = kwargs.get("log_epochs", 100)
        #传入模型保存路径，如果没有传入值则默认为"best_model.pdparams"
        save_path = kwargs.get("save_path", "best_model.pdparams")
        #梯度打印函数，如果没有传入则默认为"None"
        print_grads = kwargs.get("print_grads", None)
        #记录全局最优指标
        best_score = 0
        #进行num_epochs轮训练
        for epoch in range(num_epochs):
            X, y = train_set
            #获取模型预测
            logits = self.model(X)
            #计算交叉熵损失
            trn_loss = self.loss_fn(logits, y).item()
            self.train_loss.append(trn_loss)
            #计算评价指标
            trn_score = self.metric(logits, y).item()
            self.train_scores.append(trn_score)
            #计算参数梯度
            self.model.backward(y)
            if print_grads is not None:
                #打印每一层的梯度
                print_grads(self.model)
            #更新模型参数
            self.optimizer.step()
            dev_score, dev_loss = self.evaluate(dev_set)
            #如果当前指标为最优指标，保存该模型
            if dev_score > best_score:
                self.save_model(save_path)
                print(f"best accuracy performence has been updated: {best_score:.5f} --> {dev_score:.5f}")
                best_score = dev_score
            if epoch % log_epochs == 0:
                print(f"[Train] epoch: {epoch}, loss: {trn_loss}, score: {trn_score}")
                print(f"[Dev] epoch: {epoch}, loss: {dev_loss}, score: {dev_score}")
                
    def evaluate(self, data_set):
        X, y = data_set
        #计算模型输出
        logits = self.model(X)
        #计算损失函数
        loss = self.loss_fn(logits, y).item()
        self.dev_loss.append(loss)
        #计算评价指标
        score = self.metric(logits, y).item()
        self.dev_scores.append(score)
        return score, loss

    def predict(self, X):
        return self.model(X)

    def save_model(self, save_path):
        torch.save(self.model.params, save_path)

    def load_model(self, model_path):
        self.model.params = torch.load(model_path)

5. activation.py

import torch

#x为tensor
def softmax(X):
    """
    输入：
        - X：shape=[N, C]，N为向量数量，C为向量维度
    """
    x_max = torch.max(X, axis=1, keepdim=True).values#N,1
    x_exp = torch.exp(X - x_max)
    partition = torch.sum(x_exp, axis=1, keepdim=True)#N,1
    return x_exp / partition

6. 该篇所有代码

# 3.3 实践：基于Softmax回归完成鸢尾花分类任务
# 3.3.1 数据处理
# Iris数据集，也称为鸢尾花数据集，包含了3种鸢尾花类别（Setosa、Versicolour、Virginica），每种类别有50个样本，共计150个样本。
# 其中每个样本中包含了4个属性：花萼长度、花萼宽度、花瓣长度以及花瓣宽度，本实验通过鸢尾花这4个属性来判断该样本的类别。
from sklearn.datasets import load_iris
import pandas
import numpy as np
import torch
import op, metric, opitimizer, RunnerV2

# 对数据集中的缺失值或异常值等情况进行分析和处理，保证数据可以被模型正常读取。代码实现如下：
iris_features = np.array(load_iris().data, dtype=np.float32)
iris_labels = np.array(load_iris().target, dtype=np.int32)
print(pandas.isna(iris_features).sum())
print(pandas.isna(iris_labels).sum())

# 从输出结果看，鸢尾花数据集中不存在缺失值的情况。

# 通过箱线图直观的显示数据分布，并观测数据中的异常值。
import matplotlib.pyplot as plt #可视化工具

# 箱线图查看异常值分布
def boxplot(features):
    feature_names = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width']

    # 连续画几个图片
    plt.figure(figsize=(5, 5), dpi=200)
    # 子图调整
    plt.subplots_adjust(wspace=0.6)
    # 每个特征画一个箱线图
    for i in range(4):
        plt.subplot(2, 2, i+1)
        # 画箱线图
        plt.boxplot(features[:, i], 
                    showmeans=True, 
                    whiskerprops={"color":"#E20079", "linewidth":0.4, 'linestyle':"--"},
                    flierprops={"markersize":0.4},
                    meanprops={"markersize":1})
        # 图名
        plt.title(feature_names[i], fontdict={"size":5}, pad=2)
        # y方向刻度
        plt.yticks(fontsize=4, rotation=90)
        plt.tick_params(pad=0.5)
        # x方向刻度
        plt.xticks([])
    plt.savefig('ml-vis.pdf')
    plt.show()

boxplot(iris_features)
# 从输出结果看，数据中基本不存在异常值，所以不需要进行异常值处理。

# 3.3.1.3 数据读取

# 加载数据集
def load_data(shuffle=True):
    '''
    加载鸢尾花数据
    输入：
        - shuffle：是否打乱数据，数据类型为bool
    输出：
        - X：特征数据，shape=[150,4]
        - y：标签数据, shape=[150]
    '''
    # 加载原始数据
    X = np.array(load_iris().data, dtype=np.float32)
    y = np.array(load_iris().target, dtype=np.float32)

    X = torch.tensor(X)
    y = torch.tensor(y)

    # 数据归一化
    X_min = torch.min(X, dim=0).values
    X_max = torch.max(X, dim=0).values
    X = (X-X_min) / (X_max-X_min)

    # 如果shuffle为True,随机打乱数据
    if shuffle:
        idx = torch.randperm(X.shape[0])
        X = X[idx]
        y = y[idx]
    return X, y

# 固定随机种子
torch.manual_seed(102)

num_train = 120
num_dev = 15
num_test = 15

X, y = load_data(shuffle=True)
print("X shape: ", X.shape, "y shape: ", y.shape)
X_train, y_train = X[:num_train], y[:num_train]
X_dev, y_dev = X[num_train:num_train + num_dev], y[num_train:num_train + num_dev]
X_test, y_test = X[num_train + num_dev:], y[num_train + num_dev:]

# 打印X_train和y_train的维度
print("X_train shape: ", X_train.shape, "y_train shape: ", y_train.shape)

# 打印前5个数据的标签
print(y_train[:5])

# 3.3.2 模型构建
# 使用Softmax回归模型进行鸢尾花分类实验，将模型的输入维度定义为4，输出维度定义为3。代码实现如下：

# 输入维度
input_dim = 4
# 类别数
output_dim = 3
# 实例化模型
model = op.model_SR(input_dim=input_dim, output_dim=output_dim)

# 3.3.3 模型训练
# 实例化RunnerV2类，使用训练集和验证集进行模型训练，共训练80个epoch，
# 其中每隔10个epoch打印训练集上的指标，并且保存准确率最高的模型作为最佳模型。代码实现如下：

# 学习率
lr = 0.2

# 梯度下降法
optimizer = opitimizer.SimpleBatchGD(init_lr=lr, model=model)
# 交叉熵损失
loss_fn = op.MultiCrossEntropyLoss()
# 准确率
metric2 = metric.accuracy

# 实例化RunnerV2
runner = RunnerV2.RunnerV2(model, optimizer, metric2, loss_fn)

# # 启动训练
runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=200, log_epochs=10, save_path="best_model.pdparams")

import plot

plot.plot(runner,fig_name='linear-acc3.pdf')

# 加载最优模型
runner.load_model('best_model.pdparams')
# 模型评价
score, loss = runner.evaluate([X_test, y_test])
print("[Test] score/loss: {:.4f}/{:.4f}".format(score, loss))

# 预测测试集数据
logits = runner.predict(X_test)
# 观察其中一条样本的预测结果
pred = torch.argmax(logits[0]).numpy()
print("pred:",pred)
# 获取该样本概率最大的类别
label = y_test[0].numpy()
print("label:",label)
# 输出真实类别与预测类别
print("The true category is {0} and the predicted category is {1}".format(label, pred))

---

习题

尝试调整学习率和训练轮数等超参数，观察是否能够得到更高的精度

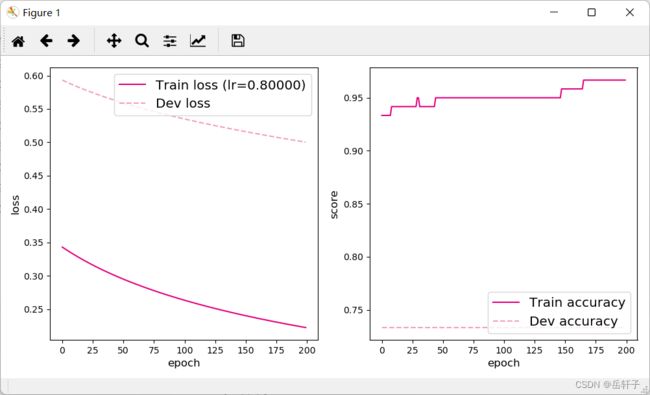
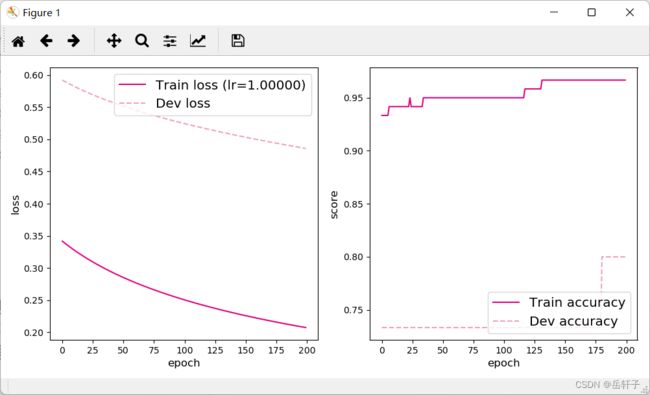
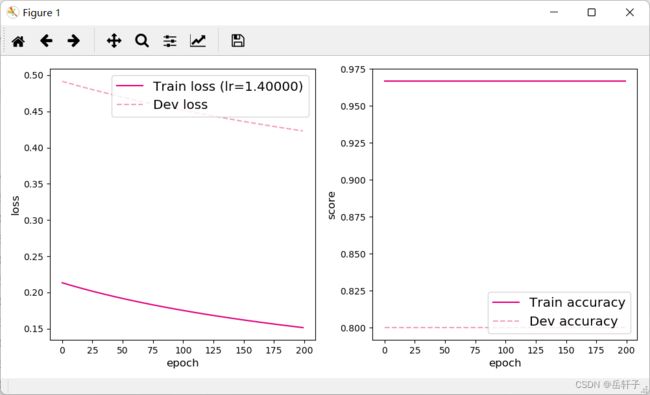
学习率

首先，我们看一下学习率的影响，这里我们循环一下（为了方便观察，内部代码有些许更改）：

# 学习率
lr2 = 0.2
for i in range(8):
    lr = lr2 * i
	# 梯度下降法
    optimizer = opitimizer.SimpleBatchGD(init_lr=lr, model=model)
	# 交叉熵损失
    loss_fn = op.MultiCrossEntropyLoss()
	# 准确率
    metric2 = metric.accuracy

	# 实例化RunnerV2
    runner = RunnerV2.RunnerV2(model, optimizer, metric2, loss_fn)

	# # 启动训练
    runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=200, log_epochs=10, save_path="best_model.pdparams")


    plot.plot(runner,fig_name='linear-accx.pdf',x = lr)

	# 加载最优模型
    runner.load_model('best_model.pdparams')
	# 模型评价
    score, loss = runner.evaluate([X_test, y_test])
    print("[Test] score/loss: {:.4f}/{:.4f}".format(score, loss))

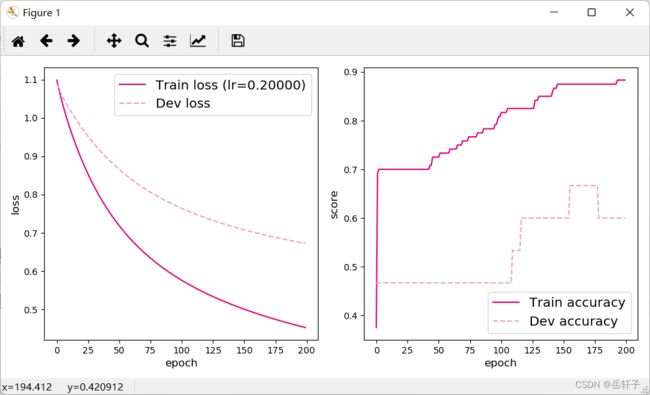
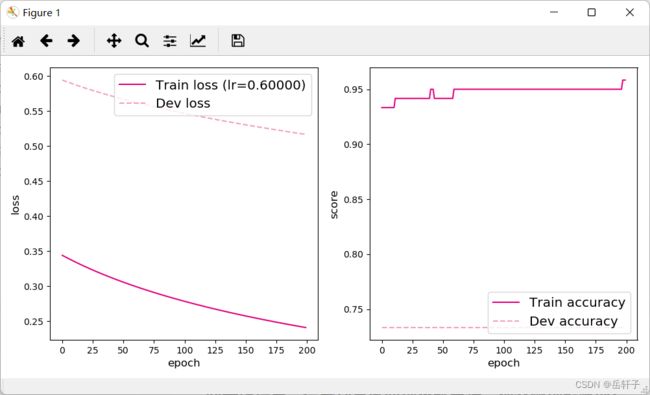
运行结果（lr为学习率）：

[Test] score/loss: 0.2000/1.0986

[Test] score/loss: 0.7333/0.5930

[Test] score/loss: 0.8667/0.4474

[Test] score/loss: 0.8667/0.4465

[Test] score/loss: 0.8667/0.4452

[Test] score/loss: 0.9333/0.3147

[Test] score/loss: 0.9333/0.3142

[Test] score/loss: 0.9333/0.3137

通过调节学习率，我们发现，学习率过低和过高都会造成训练模型变差，当训练模型没有达到预取效果时，我们可以通过调整学习率来改变训练模型，让其向着预期效果学习

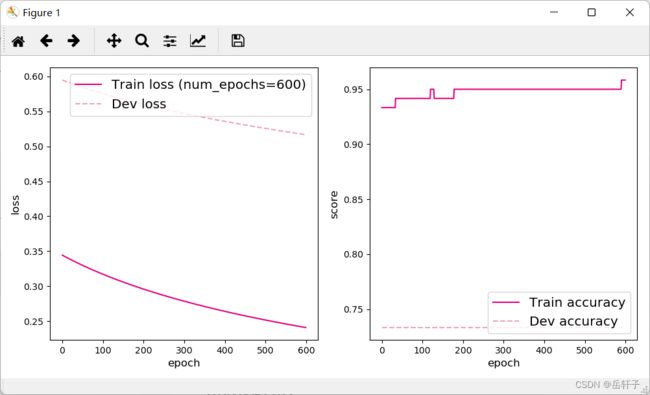
训练轮数

下面，我们来调节一下训练轮数：

# 学习率
lr = 0.2
num_epochs2 = 200
for i in range(1,8):
    num_epochs = num_epochs2 * i
# 梯度下降法
    optimizer = opitimizer.SimpleBatchGD(init_lr=lr, model=model)
# 交叉熵损失
    loss_fn = op.MultiCrossEntropyLoss()
# 准确率
    metric2 = metric.accuracy

# 实例化RunnerV2
    runner = RunnerV2.RunnerV2(model, optimizer, metric2, loss_fn)

# # 启动训练
    runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=num_epochs, log_epochs=10, save_path="best_model.pdparams")


    plot.plot(runner,fig_name='linear-accx.pdf',x = num_epochs)

# 加载最优模型
    runner.load_model('best_model.pdparams')
# 模型评价
    score, loss = runner.evaluate([X_test, y_test])
    print("[Test] score/loss: {:.4f}/{:.4f}".format(score, loss))

运行结果：

[Test] score/loss: 0.9333/0.3125

[Test] score/loss: 0.8667/0.4478

[Test] score/loss: 0.8667/0.4475

[Test] score/loss: 0.8667/0.4472

[Test] score/loss: 0.9333/0.3150

[Test] score/loss: 0.9333/0.3149

[Test] score/loss: 0.9333/0.3149

通过调整训练轮数我们发现，当训练轮数少时，误差较大；当训练轮数过多时，误差为0，过拟合了。当我们训练模型差时，可以提高训练轮数；当我们训练模型太好的时候，我们有可能过拟合了。

注： 训练轮数的调节不要从0开始

---

总结

通过该章的学习，我学会使用Softmax回归和Logistic回归的使用，和实践的应用，了解了训练轮数和学习率对训练模型的影响。加深了实践过程步骤，也更加深刻的了解了深度学习的过程。

内容太多了，如果太多了，可能会没有耐心看完，而且查找也不是很方便。
这里我分成了上中下三篇，分别为基于Logistic回归的二分类任务（上篇），基于Softmax回归的多分类任务（中篇），实践：基于Softmax回归完成鸢尾花分类任务（下篇）。

上篇：深度学习 第3章线性分类 实验四 pytorch实现 Logistic回归 上篇
中篇：深度学习 第3章线性分类 实验四 pytorch实现 Softmax回归 中篇

---

创作不易，如果对你有帮助，求求你给我个赞！！！
点赞 + 收藏 + 关注！！！
如有错误与建议，望告知！！！（将于下篇文章更正）
请多多关注我！！！谢谢！！！