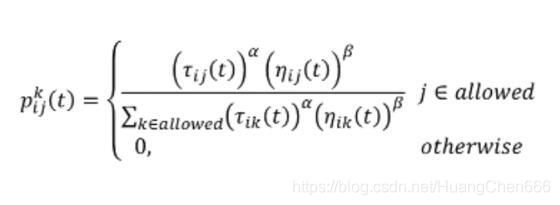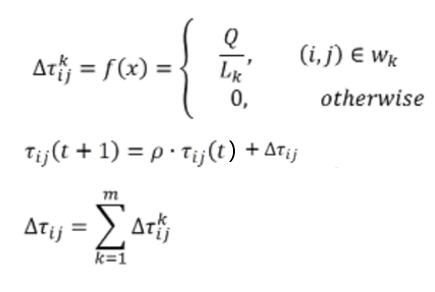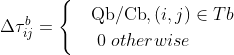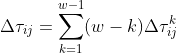蚁群优化算法（ACO）
背景知识
蚁群优化算法是Marco Dorigo 受到蚂蚁寻找食物发现路径的行为启发，在博士论文提出的算法，是一种用来寻找优化路径的概率型算法，刚开始是为了解决 TSP(旅行商问题) ，即旅行家要旅行n个城市，要求各个城市经历且仅经历一次然后回到出发城市，并要求所走的路程最短。目前其应用扩展到了优化问题领域的各个方面，算法设计得到不断的改进，逐渐构筑起一套成熟的算法框架，成为组合优化领域最具有潜力的算法之一。组合优化问题：如旅行商问题、指派问题、Job—shop调度问题、车辆路由问题、图着色问题和网络路由问题等。
优点：
- 是一种本质上的并行算法，即各个蚂蚁各自寻找路径。
- 是一种自组织的算法，所谓自组织就是没有外界干预，自己从无序到有序的过程。
- 具有较强的鲁棒性。
- 是一种正反馈算法。（蚂蚁能够最终找到最优路径，直接依赖于其在路径上信息素的堆积，而信息素的堆积是一个正反馈的过程。）
缺点：
- 收敛速度慢（因为需要等，但是节奏可以自己控制）
- 易陷入局部最优（可以通过增加跳转目标的随机性改进）
- 对于解空间为连续的优化问题不适用（蚁群优化算法适用于离散问题，粒子群算法适合解连续空间问题，参照上一篇）
算法思想
情景：蚂蚁寻找食物源，蚂蚁到达食物源患有多条路径，蚂蚁在选择路径时回释放一种信息素，此信息素会随时间含量不断减少，如此路径较短的蚂蚁往复次数多，留下的信息素含量不断增多，而蚂蚁会做出选择走信息素多的路，随时间发展，路径短的蚂蚁会越来越多。
思想抽象：蚂蚁的行走路径表示待优化问题的可行解，整个蚂蚁群体的所有路径构成待优化问题的解空间。由于路径较短的蚂蚁释放的信息素量较多，随着时间的推进，较短的路径上累积的信息素浓度逐渐增高，选择该路径的蚂蚁个数也愈来愈多。最终，整个蚂蚁会在正反馈的作用下集中到最佳的路径上，此时对应的便是待优化问题的最优解。
定义对照表：
| 蚁群觅食 | 蚁群优化算法 |
| 蚁群 | 种群规模（搜索空间的一组有效解） |
| 觅食空间 | 问题搜索空间（解的规模，维度） |
| 信息素 | 信息素浓度变量 |
| 所有的路径 | 有效解 |
| 最短路径 | 问题最优解 |
蚁群算法形式化：
- 每只蚂蚁对应一个计算智能体
- 蚂蚁根据概率选择位置进行移动
- 在经过的路径上留下“信息素”
- “信息素”会随时间挥发
- “信息素”浓度大的路径在后序选择中会以更高的概率被选中
算法流程
- 对相关参数进行初始化，包括蚁群规模、信息素因子、启发函数因子、信息素的挥发因子、信息素常数、以及最大迭代次数等，以及将数据读入程序，并进行预处理：比如将城市的坐标信息转化为城市间的距离矩阵。
- 随机将蚂蚁放于不同的出发点，对每个蚂蚁计算其下个访问城市，直到有蚂蚁访问完所有的城市。
- 计算各蚂蚁经过的路径长度Lk，记录当前迭代次数最优解，同时对路径上的信息素浓度进行更新。
- 判断是否到达迭代次数，若否，返回步骤2；是，结束程序。
- 输出结果，并根据需要输出寻优过程中的相关指标，如运行时间、迭代次数等。
旅行商问题
核心是蚁群优化算法的两个公式，一个是路径构建（计算选择城市概率的），另一个是更新信息素的。
- N个城市的有向图 G=(N, A) 其中N={1,2....n} A={(i,j) | i,j
N} - 城市之间的距离表示为
即节点 i 和节点 j 的距离 - 目标函数
目标函数是每个城市都经过一次的总路程，i1,i2 表示第一个和第二个到达的城市。 - w=(i1，i2, ...in) 为城市1,2...n 的一个排列（即TSP问题任意可行解）。
路径构建
首先呢我们将m只蚂蚁随机放置在n个城市上，我们需要让蚂蚁去移动，那么就要计算蚂蚁选择移动的下一个城市的概率，位于城市 i 的第 k 只蚂蚁选择下一个城市 j 的概率为：
公式分析： 蚂蚁选择下一个城市的概率是与信息素成正比的，信息素浓度越大被选择的几率越大。城市之间的距离越短，被选择的几率越大。选择因素有权重，引入了次幂
。
表示时间 t 时刻，边（i,j）上的信息素浓度
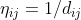根据距离定义的启发信息- 为两个常数，反映信息素和启发信息的相对重要性
- allowed 为尚未访问的节点集合
信息素更新
通过上面的式子可以观察到城市之间的距离事固定的，所以如果信息素也不变，则每只蚂蚁到达同一个城市后的选择都是一样的了，这不是我们目的，所以需要更新概率则只能更新
（信息素）
- 在算法初始化时，问题空间中所有的边上的信息素都被初始化为C。 注：C太小，算法容易早熟，会快速进入局部最优，反之，信息素对搜索方向的指导作用太低。
- 每一轮过后，问题空间中的所有路径上的信息素都会发生蒸发。信息素蒸发是自然界本身固有的特征，在算法中能够帮助避免信息素的无限积累，使得算法可以快速丢弃之前构建过的较差的路径。
- 所有的蚂蚁根据自己构建的路径长度在它们本轮经过的边上释放信息素，蚂蚁构建的路径越短、释放的信息素就越多。一条边被蚂蚁爬过的次数越多、它所获得的信息素也越多。
当所有的蚂蚁都经过了所有的城市，则开始进行信息素的更新，按照以下公式：
- Q 为常数,
表示第 k 只蚂蚁在本轮迭代走过的路径，
为路径长度， 
为小于1 的常数，反映信息素的挥发速度 - Q/ 表示第 k 只蚂蚁在该路径上留下的平均信息素
公式分析：信息素更新理解为，这一刻 ij 路径上的信息素浓度等于上一刻的信息素浓度乘以挥发速度 ，再加上上一时间段内所有蚂蚁在该路径上释放的的信息素浓度之和。
算法测试
测试代码
clc;clear;
t0=clock; %用于计时
%% 初始化城市信息
n=30; %定义城市个数
city=[(randperm(100,n))',(randperm(100,n))']; %获取城市坐标 产生n个1-100的随机数，不重复
figure('name','蚁群优化算法');
plot(city(:,1),city(:,2),'o'); %描点 city--（30，2）
for i=1:n
text(city(i,1)+0.5,city(i,2),num2str(i)); %标号
end
title('蚁群优化算法');
%设置横纵坐标范围
grid on %网格线
hold on %图像保持而不被刷新
%% 求出各个城市之间的距离
D=zeros(n,n); %新建一个n*n的矩阵存放距离
for i=1:n
for j=1:n
if i~=j
D(i,j)=sqrt(sum((city(i,:)-city(j,:)).^2));
else
D(i,j)=eps; %设置成一个很小的数，但不能为0，因为后面分母中会用到
end
end
end
%% 初始化参数
m=75; %蚂蚁数量
alpha = 1; %信息素重要程度因子
beta = 5; %启发函数重要程度因子
rho = 0.2; %信息素挥发因子
Q=10; %常系数
Eta = 1./D; %启发函数(距离的倒数)
Tau = ones(n,n); %信息素矩阵(初始时每条路上的信息素都设为1)
Table = zeros(m,n); %路径记录表，记录m个蚂蚁走过的路径
% iter = 1; %迭代次数初值
iter_max = 100; %最大迭代次数
Route_best = zeros(iter_max,n); %各代最佳路径
Length_best = zeros(iter_max,1); %各代最佳路径的长度
Length_ave = zeros(iter_max,1); %各代路径的平均长度
%% 迭代寻找最佳路径
for iter=1:iter_max
%随机产生蚂蚁的起点城市
for i=1:m
Table(i,1)=randperm(n,1); %产生一个0-n=30 的随机数 75*30
end
citys_index=1:n; %定义全部城市索引
for i=1:m %遍历所有蚂蚁
for j=2:n %遍历其他所有城市
tabu=Table(i,1:(j-1)); %已访问城市(禁止访问表)
allow=citys_index(~ismember(citys_index,tabu)); %除去已访问城市(待访问城市)
P=allow; %存放概率，定义成什么都可以，只要和allow长度一样
%计算城市间的选择概率
for k=1:length(allow)
%tabu(end)代表该蚂蚁此刻所在城市，allow(k)代表该蚂蚁即将去向的城市
P(k)=Tau(tabu(end),allow(k))^alpha*Eta(tabu(end),allow(k))^beta;
end
P=P/sum(P); %得到最终去往其他城市的概率集合
Pc=cumsum(P); %累计概率
%轮盘赌选择下一个城市
target_index=find(Pc>=rand); %从累计概率中找出大于随机值的情况
target=allow(target_index(1)); %取出第一个即为轮盘赌的结果
Table(i,j)=target; %确定第i只蚂蚁去往的第j-1个城市
end
end
%每只蚂蚁周游一遍后计算每只蚂蚁的路径长度
Length=zeros(m,1);
for i=1:m
for j=1:(n-1)
Length(i)=Length(i)+D(Table(i,j),Table(i,j+1));
end
%最后加上最后一个点回到起点的距离
Length(i)=Length(i)+D(Table(i,n),Table(i,1));
end
%% 计算最短路径距离及平均距离
[min_length,min_index]=min(Length); %取出最短路径及其下标
if iter==1
Length_best(iter)=min_length; %保存此次最短路径距离
else
Length_best(iter)=min(Length_best(iter-1),min_length); %选择本次和上次中最短路径较小的
end
Route_best(iter,:)=Table(min_index,:); %保存此次最短路线路径
Length_ave(iter)=mean(Length); %保存此次路线距离平均值
%% 更新信息素
Tau_Ant=Q./Length; %每条蚂蚁在路径上留下的信息素浓度
Tau_Temp=zeros(n,n);
for i=1:m
for j=1:n-1
%更新信息素
Tau_Temp(Table(i,j),Table(i,j+1))=Tau_Temp(Table(i,j),Table(i,j+1))+Tau_Ant(i);
end
%最后更新最后一个节点到起点的信息素
Tau_Temp(Table(i,n),Table(i,1))=Tau_Temp(Table(i,n),Table(i,1))+Tau_Ant(i);
end
Tau=(1-rho)*Tau+Tau_Temp; %信息素挥发后再加上新增的信息素
Table = zeros(m,n); %清空路线，进行下一轮周游
end
%% 命令行窗口显示结果
[min_length,min_index]=min(Length_best); %取出最短路径及其下标
Finnly_Route=Route_best(min_index,:);
last_time=etime(clock,t0);
disp(['最短距离为：' num2str(min_length)]);
disp(['最短路径为：' num2str(Finnly_Route)]);
disp(['运行时间：' num2str(last_time) '秒']);
%% 绘图
plot([city(Finnly_Route,1);city(Finnly_Route,1)],...
[city(Finnly_Route,2);city(Finnly_Route,2)],'bo-'); %描点
text(city(Finnly_Route(1),1),city(Finnly_Route(1),2),' 起点');
text(city(Finnly_Route(end),1),city(Finnly_Route(end),2),' 终点');
figure(2);
subplot(1,2,1); %显示在一行两列图像中的第一列
plot(Length_best);
xlabel('迭代次数');
ylabel('最短距离');
title('最短距离收敛曲线');
subplot(1,2,2); %显示在一行两列图像中的第二列
plot(Length_ave);
xlabel('迭代次数');
ylabel('平均距离');
title('平均距离收敛曲线');总结：
- 蚂蚁数量m；m过大时，会导致搜索过的路径上信息素变化趋于平均，难以找到目标路径；m过小时，易使未被搜索到的路径信息素减小到0，这样可能会出现早熟，找不到全局最优解。蚂蚁数设定为城市数量的1.5倍比较合适
- 信息素重要程度因子alpha：信息素因子alpha反映了蚂蚁在移动过程中所积累的信息量在指导蚁群搜索中的相对重要程度，alpha值过大，蚂蚁选择以前走过的路径概率大，搜索随机性减弱；值过小，则会类似于贪婪算法，使搜索过与陷入局部最优。信息素因子大致选择在[1，4]区间
- 启发函数重要程度因子beta；启发函数因子beta反映了启发式信息在指导蚁群搜索过程中的相对重要程度，其大小反映的是蚁群寻优过程中先验性和确定性因素的作用强度。beta过大时，虽然收敛速度会加快，但容易陷入局部最优；过小时，容易陷入随机搜索，找不到最优解。启发函数因子选择在[3，5]区间
- 信息素挥发因子rho：信息素挥发因子表示信息素的消失水平,它的天小直接关系到蚁群算法的全局搜索能力和收敛速度。信息素挥发因子选择[0.2，0.5]区间
算法改进思路
精英策略的蚂蚁系统(Elitist Ant System, EAS)
问题：当城市的规模较大时，问题的复杂度呈指数级增长，仅仅靠这样一个基础单一的信息素更新机制引导搜索偏向，搜索效率有瓶颈。
方法：
- 通过一种“额外的手段”强化某些最有可能成为最优路径的边，让蚂蚁的搜索范围更快、更正确的收敛。
- 在算法开始后即对所有已发现的最好路径给予额外的增强，并将随后与之对应的行程记为Tb(全局最优行程)；
- 当进行信息素更新时，对这些行程予以加权，同时将经过这些行程的蚂蚁记为“精英”，从而增大较好行程的选择机会。
信息素更新公式：
特点：能快速的获得更好的解，如果选择的精英过多会较早收敛与局部最优解。
基于排列的蚂蚁系统(Rank-based AS, ASrank )
人们提出了在精英策略的基础上，对其余边的信息素更新机制加以改善
- 与精英策略相似，总更新较好的路径上的信息素，选择标准是路程长度
- 每只蚂蚁释放信息素的强度通过下列公式决定。
注：w为每次迭代后释放信息素的蚂蚁总数，一般设置为6
最大最小蚂蚁系统(MAX-MIN Ant System, MMAS)
问题：
- 大规模的TSP，由于搜索蚂蚁的个数有限，而初始化时蚂蚁的分布是随机的，这会不会造成蚂蚁只搜索了所有路径 中的小部分就以为找到了最好的路径，所有的蚂蚁都很快聚集在 同一路径上，而真正优秀的路径并没有被搜索到呢？
- 当所有蚂蚁都重复构建着同一条路径的时候，意味着算法的已经进入停滞状态。此时不论是基本AS、EAS还是ASrank ， 之后的迭代过程都不再可能有更优的路径出现。这些算法收敛的效果虽然是“单纯而快速的”，但我们都懂得欲速而不达的道理，我们有没有办法利用算法停滞后的迭代过程进一步搜索以保证找到更接近真实目标的解呢？
对于最大最小蚂蚁系统
- 该算法修改了AS的信息素更新方式，只允许迭代最优蚂蚁（在本次迭代构建出最短路径的蚂蚁），或者至今最优蚂蚁 释放信息素
- 借鉴于精华蚂蚁系统，但又有细微的不同。在EAS中，只允许至今最优的蚂蚁释放信息素，而在MMAS中，释放信息素的不仅有可能是至今最优蚂蚁，还有可能是迭代最优蚂蚁。
- 实际上，迭代最优更新规则和至今最优更新规则在MMAS中是交替使用的,这两种规则使用的相对频率将会影响算法的搜索效果。只使用至今最优更新规则进行信息素的更新，搜索的导向性很强，算法会很快的收敛到Tb附近，反之，如果只使用迭代最优更新规则，则算法的探索能力会得到增强，但搜索效率会下降。
- 路径上的信息素浓度被限制在[min，max ]范围内
- 是为了避免某些边上的信息素浓度增长过快，出现算法早熟现象
- 蚂蚁是根据启发式信息和信息素浓度选择下一个城市的。启发式信息的取值范围是确定的。
- 当信息素浓度也被限定在一个范围内以后，位于城市i的蚂蚁k选择城市j作为下一个城市的概率pk(i,j)也将被限制在一个区间内。
- 信息素的初始值被设为其取值上限，这样有助于增加算法初始阶段的搜索能力
- 使得算法在初始阶段，问题空间内所有边上的信息素均被初始化τmax的估计值，且信息素蒸发率非常小（在MMAS中，一般将蒸发率设为0.02）。
- 算法的初始阶段，不同边上的信息素浓度差异只会缓慢的增加，因此，MMAS在初始阶段有着较基本AS、EAS和ASrank更强搜索能力。
- 增强算法在初始阶段的探索能力有助于蚂蚁“视野开阔地”进行全局范围内的搜索，随后再逐渐缩小搜索范围，最后定格在一条全局最优路径上。
之前的蚁群算法，包括AS、EAS以及ASrank，都属于“一次性探索”，即随着算法的执行，某些边上的信息素量越来越小，某些路径被选择的概率也越来越小，系统的探索范围不断减小直至陷入停滞状态。
- 为了避免搜索停滞，问题空间内所有边上的信息素都会被重新初始化
- 当算法接近或者是进入停滞状态时，问题空间内所有边上的信息素浓度都将被初始化，从而有效的利用系统进入停滞状态后的迭代周期继续进行搜索，使算法具有更强的全局寻优能力。
蚁群系统（Ant Colony System）
上述EAS、ASrank 以及MMAS都是对AS进行了少量的修改而获得了更好的性能。1997年，蚁群算法的创始人Dorigo在Ant colony system：a cooperative learning approach to the traveling salesman problem一文中提出了一种新的具有全新机制的ACO 算法——蚁群系统，是蚁群算法发展史上的又一里程碑。
ACS与AS之间存在三方面的主要差异
- 使用一种伪随机比例规则选择下一个城市节点， 建立开发当前路径与探索新路径之间的平衡
- 信息素全局更新规则只在属于至今最优路径的边上蒸发和释放信息素
- 新增信息素局部更新规则，蚂蚁每次经过空间内的某条边，他都会去除该边上的一定量的信息素，以增加后续蚂蚁探索其余路径的可能性。
状态转移规则
一只蚂蚁从节点 i 到下一个节点遵循以下规则（伪随机比例规则）
![j=arg\max_{allowed}{ [\tau_{ij} *\eta_{ij}^{\beta }]} ---if q<q_{0}](http://img.e-com-net.com/image/info8/fadf1781326442eb990f68ee60fbb78b.gif){kind=small}
- q 是【0,1】区间均匀分布的随机数
的大小决定了利用先验只是与探索新路径之间的相对重要性
信息素全局更新规则
- ACS 只增强属于全局最优解的路径上的信息素，更新公式如下：
- 注：0<<1 是信息素的挥发参数，Cb是从寻找开始到当前为止全局最优的路径长度
信息素局部更新规则
- 引入了负反馈机制，每当一只蚂蚁从一个节点移动到另一个节点时，该路径上的信息素都按照如下公式被相应的消除一部分，实现信息素的局部调整，减小已选择过的路径再次被选择的概率
小白一个，参照多篇，自我总结，侵删（私聊我），勿喷！！！