lstm时间序列预测+GRU（python）

可以参考新发布的文章
1.BP神经网络预测（python）
2.mlp多层感知机预测（python）
下边是基于Python的简单的LSTM和GRU神经网络预测，多输入多输出，下边是我的数据，红色部分预测蓝色
2,3行输入，第4行输出
3,4行输入，第5行输出
…以此类推

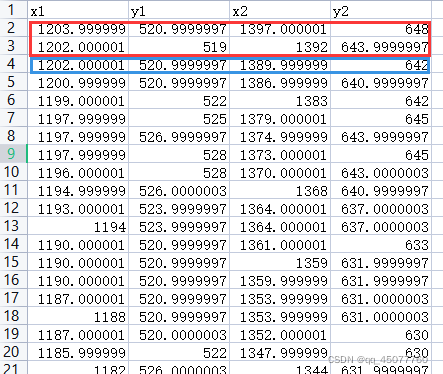
简单利索，直接上代码

import matplotlib
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import sklearn.metrics
from IPython.core.display import SVG
from keras.layers import LSTM, Dense, Bidirectional
from keras.losses import mean_squared_error
from keras.models import Sequential
from keras.utils.vis_utils import model_to_dot, plot_model
from matplotlib import ticker
from keras import regularizers
from pandas import DataFrame, concat
from sklearn import metrics
# from sklearn.impute import SimpleImputer
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
#from statsmodels.tsa.seasonal import seasonal_decompose
import tensorflow as tf
import seaborn as sns
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['axes.unicode_minus'] = False


def load_data(path):
    data_origin = pd.read_excel(path)

    # 把object类型转换为float
    data_origin = DataFrame(data_origin, dtype=float)
    # 打印显示所有列
    pd.set_option('display.max_columns', None)
    # 获得数据的描述信息
    # print(data_dropDate.describe())
    return data_origin

#单维最大最小归一化和反归一化函数
# 对于训练数据进行归一化之后。使用训练数据的最大最小值（训练数据的范围）对于测试数据进行归一化 保留周期和范围信息
def Normalize(df,low,high):
    delta = high - low
    for i in range(0,df.shape[0]):
        for j in range(0,df.shape[1]):
            df[i][j] = (df[i][j]-low[j])/delta[j]
    return df
# 定义反归一化函数
def FNormalize(df,low,high):
    delta = high - low
    for i in range(0,df.shape[0]):
        for j in range(0,df.shape[1]):
            df[i][j] = df[i][j] * delta[j] + low[j]
    return df


# 数据集转换成监督学习问题
# 数据集转换成监督学习函数
def series_to_supervise(data,n_in=1,n_out=1,dropnan=True):
    '''该函数有四个参数：

    data：作为列表或 2D NumPy 数组的观察序列。必需的。
    n_in ：作为输入 ( X )的滞后观察数。值可能在 [1..len(data)] 之间可选。默认为 1。
    n_out：作为输出的观察数（y）。值可能在 [0..len(data)-1] 之间。可选的。默认为 1。
    dropnan：布尔值是否删除具有 NaN 值的行。可选的。默认为真。
    该函数返回一个值：

    return：用于监督学习的系列 Pandas DataFrame。'''
    n_vars = 1 if type(data) is list else data.shape[1]
    df = DataFrame(data)
    cols , names = list(),list()
    # input sequence(t-n,...,t-1)
    for i in range(n_in,0,-1):
        cols.append(df.shift(i))
        names += [('var%d(t-%d)' %(j+1,i)) for j in range(n_vars)]
    # forecast sequence (t, t+1, ... t+n)
    for i in range(0, n_out):
        cols.append(df.shift(-i))
        if i == 0:
            names += [('var%d(t)' % (j+1)) for j in range(n_vars)]
        else:
            names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)]
    # put it all together
    agg = concat(cols, axis=1)
    agg.columns = names
    # drop rows with NaN values
    if dropnan:
        agg.dropna(inplace=True)
    return agg
# 定义一个名为split_sequences()的函数，它将采用我们定义的数据集，其中包含时间步长的行和并行序列的列，并返回输入/输出样本。
# split a multivariate sequence into samples
def split_sequences(sequences, n_steps):
    X, y = list(), list()
    for i in range(len(sequences)):
        # # find the end of this pattern
        end_ix = i + n_steps
        if end_ix > len(sequences)-n_steps:
            break
        # gather input and output parts of the pattern
        seq_x,seq_y = sequences[i:end_ix,:-1],sequences[end_ix,:-1]
        X.append(seq_x)
        y.append(seq_y)
    return np.array(X),np.array(y)

path = 'E:/YOLO/yolov5-master/digui/1/origin.xlsx'
data_origin = load_data(path)
print(data_origin.shape)

# 先将数据集分成训练集和测试集
train_Standard = data_origin.iloc[:60,:]  # （145,23）,前60行
test_Standard = data_origin.iloc[60:,:]  # （38,23），后边

# 再转换为监督学习问题
n_in = 2
n_out = 1
train_Standard_supervise = series_to_supervise(train_Standard,n_in,n_out)  # (144,46)
test_Standard_supervise = series_to_supervise(test_Standard,n_in,n_out)  # (37,46)
print('test_Standard_supervise')
print(test_Standard_supervise.head())

# 将训练集和测试集分别分成输入和输出变量。最后，将输入（X）重构为 LSTM 预期的 3D 格式，即 [样本，时间步，特征]
# split into input and output
train_Standard_supervise = train_Standard_supervise.values
test_Standard_supervise = test_Standard_supervise.values
train_X,train_y = train_Standard_supervise[:,:8],train_Standard_supervise[:,8:]
test_X,test_y = test_Standard_supervise[:,:8],test_Standard_supervise[:,8:]



#归一化
scaler = StandardScaler()
train_X=scaler.fit_transform(train_X)
train_y = train_y.reshape(train_y.shape[0],4)
train_y=scaler.fit_transform(train_y)
test_X=scaler.fit_transform(test_X)
test_y = test_y.reshape(test_y.shape[0],4)
test_y=scaler.fit_transform(test_y)


# reshape input to be 3D [samples,timeseps,features]
train_X = train_X.reshape((train_X.shape[0],1,train_X.shape[1]))
test_X = test_X.reshape((test_X.shape[0],1,test_X.shape[1]))
print(train_X.shape,train_y.shape,test_X.shape,test_y.shape)  #(145, 1, 22) (145,) (38, 1, 22) (38,)
groups = [10]
i = 1
plt.figure()
for group in groups:
    # 定义模型
    model = Sequential()
    # 输入层维度：input_shape（步长，特征数）
    model.add(LSTM(64, input_shape=(train_X.shape[1], train_X.shape[2]),recurrent_regularizer=regularizers.l2(0.4)))  #,return_sequences=True
    model.add(Dense(4))
    model.compile(loss='mae', optimizer='adam')
    # 拟合模型
    history = model.fit(train_X, train_y, epochs=100, batch_size=group, validation_data=(test_X, test_y))

    plt.subplot(len(groups),1,i)
    plt.plot(history.history['loss'], label='train')
    plt.plot(history.history['val_loss'], label='test')
    plt.xlabel('epoch')
    plt.ylabel('loss')
    plt.title('batch_size = %d' %group)
    plt.legend()
    i += 1
plt.show()


# 预测测试集
yhat = model.predict(test_X)
test_X = test_X.reshape((test_X.shape[0], test_X.shape[2]))
# invert scaling for forecast
# invert scaling for actual
test_y = test_y.reshape((len(test_y), 4))
yhat=scaler.inverse_transform(yhat)
test_y=scaler.inverse_transform(test_y)
# calculate RMSE
#print(test_y)
#print(yhat)

rmse = np.sqrt(mean_squared_error(test_y, yhat))
mape = np.mean(np.abs((yhat-test_y)/test_y))*100
print('=============rmse==============')
print(rmse)
print('=============mape==============')
print(mape,'%')
print("R2 = ",metrics.r2_score(test_y, yhat)) # R2
# 画出真实数据和预测数据的对比曲线图
plt.plot(test_y,color = 'red',label = 'true')
plt.plot(yhat,color = 'blue', label = 'pred')
plt.title('Prediction')
plt.xlabel('Time')
plt.ylabel('value')
plt.legend()
plt.show()

这是出来的训练集和测试集损失图

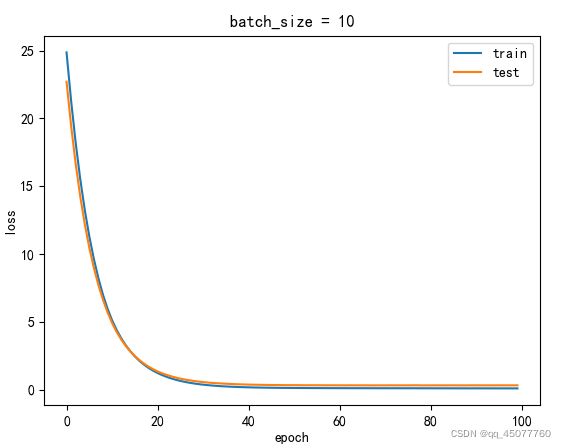
下边是预测值和真实值的结果图，其中
mape=0.15912692740815412 %
R2 = 0.9762727107502187

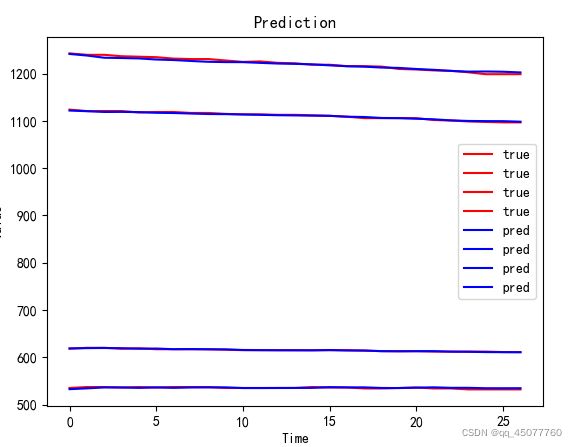
GRU的修改
把

    model = Sequential()
    # 输入层维度：input_shape（步长，特征数）
    model.add(LSTM(64, input_shape=(train_X.shape[1], train_X.shape[2]),recurrent_regularizer=regularizers.l2(0.4)))  #,return_sequences=True
    model.add(Dense(4))
    model.compile(loss='mae', optimizer='adam')
    # 拟合模型
    history = model.fit(train_X, train_y, epochs=100, batch_size=group, validation_data=(test_X, test_y))

改成

model = Sequential()
model.add(Dense(128, input_shape=(train_X.shape[1], train_X.shape[2]),
                activation='relu'
                )
          )
model.add(Dense(64, activation='relu'))
model.add(Dense(1,
                activation='sigmoid'
                ))
model.compile(loss='mae',optimizer='rmsprop')                                 
# 拟合模型
batchsize = 10
history = model.fit(train_X, train_y, epochs=100, batch_size=batchsize, validation_data=(test_X, test_y))

剩下的就剩调参了