代数多重网格法简介（Algebraic Multigrid）

        近来一直在学习代数多重网格方法，形成了一些心得拿出来分享给大家，希望能够帮到想快速了解代数多重网格方法的人，欢迎评论或者私信。

目录

引入

代数多重网格法简介

AMG实现详解

     粗网格生成 

插值算子构建

求解阶段

AMG并行化

---

引入

        首先在了解代数多重网格（AMG）之前我们首先应该先了解什么是多重网格法（MG）。

        多重网格法（multi-grid method）是求解偏微分问题离散方程的一种快速迭代方法，最初是用于求解由椭圆边值问题离散化而得的线性代数方程组，现在也很好地被应用于各种大型线性代数方程组迭代求解。比如对于形如Au=b的线性方程组，在系数矩阵A的规模不大时，我们可以采用高斯分解法、QR分解法、矩阵求逆法来精确求解，但是当A的维度比较大时，精确求解的时间复杂度往往是我们无法承受的（LU分解时间复杂度为O（n³））。所以我们需要通过计算机迭代求解得到近似值。

        通常的迭代方法(比如雅可比迭代法，高斯一塞德尔迭代法以及SOR法等)都是在一个固定网格上的方程组的迭代方法，这些方法能够快速迭代清除网格的高频误差，但对于低频误差不能很好清除导致收敛很慢。不同于 Jacobi 迭代法和 Gauss-Seidel 迭代法，Multigrid Method 没有具体的公式形式，而是一整套求解的思路，求解过程中会利用到如 Jacobi 和 Gauss-Seidel 等基本的迭代方法。多重网格法可以通过粗网格和细网格之间的转换，在粗网格上迭代得到精确解，再将其返回到细网格上作为初始解，可以有效地提高迭代算法的收敛速度。链接：多重网格法参考资料

        而代数多重网格法（AMG）就是多重网格法的一种， AMG仅利用代数方法来构造多层网格，无需利用几何网格信息（也可以依赖第一层网格信息）。AMG方法即保持了GMG方法良好的算法可扩展能力，又可作为即插即用的黑盒子解法器，相对于GMG方法，其健壮性大大增强。尤其是AMG能够方便和有效地处理很多具有复杂区域、非结构网格和非光滑系数问题,从而受到实际应用的欢迎（美国能源部重点项目，多个商用工业软件都内置AMG求解器，比如ansys等）。参考资料链接

代数多重网格法简介

          求解Au=b的多重网格法大致可以被分为五个组件：

       其中m可以看作一个网格点为与已知矩阵有关的有向图结点的虚构网格，Im+1/m是实现从粗网格到细网格间转换的插值算子，Im/m+1是从细网格到粗网格转换的限制算子，Am就是不同网格对应的系数矩阵，而Gm是我们选定的光滑方法（相当于一种迭代方法），通常可以是jacobi方法、Gauss- seidel方法等。

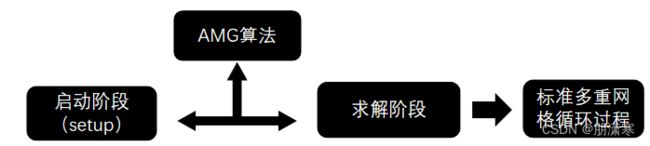
         代数多重网格法的实现过程可以被大致分为两部分：

         第一部分是setup也就是准备阶段，对于Au=b这个方程，我们通过代数方法对系数矩阵A进行操作，生成越来越粗糙（相当于矩阵维数越来越小）的多级系数矩阵，在图论里每个矩阵都有其对应的邻接图，这个图就相当于这个矩阵对应的网格，也就相当于获得了多层的网格，并且也建立起不同网格间的转换关系。

        第二部分是求解阶段，这部分一般都采用标准的多重网格循环过程，常用的循环方式有V-Cycle，F-Cycle完全多重网格循环，W-Cycle等，详细可以参考：多重网格法

         对于AMG重点是其第一部分，在实现阶段这部分往往也占据了大部分的时间，对于一些超大型方程组占比甚至可能将近80%。

AMG实现详解

         这部分我将粗略介绍AMG是如何启动的，如果对此方向不做研究可以略去。

     粗网格生成 

        这部分介绍如何通过代数手段生成多级粗网格矩阵。1987年 J.W.Ruge和K.Stuben提出了AMG的经典之作，其中就给出了一种生成粗网格的方法，我们可以称为R.S粗化算法，其数学描述比较复杂：

           我们可以把它转化为简单的表述方式：

         CR1：对每个细网格点，它的强连接点要么是粗网格点，要么它与一个粗网格点是强连接关系。

         CR2：粗网格点集应该是具有这种性质的所有点的最大子集，在粗网格点集中不能存在两个互相强连接的点。

         或许大家还是不太明白它在说什么，我们可以把系数矩阵A的一行或者一列看作网格中的一个点，aij ≠0就相当于i、j两点间有连接关系，而所谓的强连接关系是通过以下式子定义的：

        其中θ是我们自定义的一个阈值，如果aij满足这个不等式关系我们就认为i、j两点之间是强连接的。根据这两个RS粗化准则，具体的粗化算法我们可以这样表述：

       1阶段粗化算法：以以CR2为指导思想，尽可能快的选取更多的粗网格点（可能不满足CR1），把它写成集合语言如下图所示：

        其中Cm为粗网格点集合（ coarse），F 为细网格点集合（fixed），Si为i的强依赖集（strong），SiT为i点的强影响集（Si的转置），对集合取模相当于求该集合中点的数量。

        2阶段粗化算法：用CR1去检测剩余的细网格点，必要时可将不满足CR1的点加入粗网格点集。这个过程比较繁琐在此不做过多介绍，其实在实践中我们也可以不适用这2阶段粗化算法，也就是实际上只使用CR2作为标准来生成粗网格，并且也取得了一定成果。

        在经典AMG方法之外还有基于光滑聚合AMG方法，非光滑聚合AMG方法等，对粗网格点的选取目前也已经有了相当丰富的手段，比如双成对聚合粗化，size2、4、8聚合粗化等等。

插值算子构建

        插值算子也是AMG方法中非常重要的一环，负责从粗网格到细网格间的转换，限制算子和插值算子互为转置关系，即R=PT。具体数学公式推导极为繁琐，我们可以想象两个网格矩阵A（m×m），Ac（n×n）间的插值算子P（m×n）有以下数学关系：

        Ac（n×n）=PT（n×m）×A（m×m）×P（m×n）

       也就是说插值算子实际上实现了这样的功能：粗网格的特定点的系数矩阵值×插值算子矩阵里的值=待插值的细网格点系数矩阵值。插值算子中实际储存了哪些粗网格点的系数矩阵值乘以对应的权重值后求和就能得到细网格点值的系数矩阵值。

       在经典AMG方法中，我们通常把待插值的细网格点ui附近的点分为以下几类：

      1、粗网格点

      2、强连接的细网格点

      3、弱连接的细网格点

      1987年给出的方法是，将3中的点与点ui间的边权重新分配给点ui，然后将2中的点与1中的点间的边权值按照边权的比例分配给1中的点，最后统计1中各粗网格点与点ui间的边权比，得到该点ui的插值权重，重复这个过程直到所有点的插值权重都被给出为止（如果待插值点本身是粗网格点，就不需要进行插值）

       基于聚合的AMG方法中经常会选择常数插值算子，也就是同属于一个聚合间的插值权重为1。

求解阶段

        求解阶段采用的是标准多重网格方法，如下图所示：

        可以理解为对细网格上的方程，先使用光滑方法（Gm）进行迭代得到一个初始解，然后将这个初始解的残差乘限制算子转化到粗网格上得到粗网格的右端向量，再在粗网格上精确求解方程，把结果u乘插值算子转化到细网格上作为初始解，再次使用光滑方法进行迭代数次得到最终结果。

AMG并行化

       我目前在做的方向和AMG并行化相关所以也简单唠两句。对于AMG的求解部分，采用的是标准多重网格循环，这部分设计到大量的矩阵与矩阵、向量间的线性运算，目前已经有相当成熟的并行化技术了（GPU：CUDA、OpenCL等 CPU：OpenMP等），效率可观。

       但对AMG的构造阶段，粗化策略的串行本性一直阻碍其应用于大规模的并行计算。目前AMG并行计算的研究主要是以发展有效的并行粗化策略为目的而展开。近年来，为了使AMG算法能够适应大规模并行计算，大量的研究工作从不同角度提出了一系列并行粗化策略,力争在算法可扩展能力和并行可扩展能力之间寻求最佳的权衡点。

       在此总结了一些已有的AMG并行算法，可以自行查阅相关文献：RS0，FSB，MSB，RS3，CLJP/PMIS，LIPP-RS，falgout等。

参考资料：

1、《代数多重网格法研究及其在预处理Krylov子空间方法中的应用》

2、《代数多重网格理论与算法及其应用》