矩阵（加速）。。。

我限定你在明天中午之前搞定这东西！毕竟之前做过了欸。矩阵，一个看起来很神奇的东西，不过我不打算花太多的时间做这个，还是图论和数论好点儿，还要复习一下之前的数据结构和dp呢。那么先谈谈定义，定义一个矩阵就是一堆数，按照矩形排列形成的集合，那么加法的话用处不大，我们单学乘法，乘法，感觉得先搞懂定义：放一下别人的说法？

理解一下啊，就是先横后竖，若是不够形象那你可以将一个矩阵转个90度再对比？其实说的也不是这个，这个定义看看就好，重要的是其的的用处。第一当然是可以维护类斐波拉契数列的式子啦，第二也可以用于维护图，第三？动态dp吧好像，不过我还没学。
还有一个问题，就是单位矩阵！这个挺重要的，对于大部分快速幂来说都需要一个单位矩阵，有人用1，有人我不说。再看看那个大佬的
P3390 【模板】矩阵快速幂重新写了一份。

#include
#define int long long 
using namespace std;
int n,m,mod=1e9+7;
struct node 
{
	int n,m,w[220][220];
};node aa,bb;
void init(node &now,int x)
{
	now.n=x,now.m=x;memset(now.w,0,sizeof(now.w));
	for(int i=1;i<=x;i++) now.w[i][i]=1;
	return ;
}
void clean(node &now)
{
	memset(now.w,0,sizeof(now.w));
	return ;
}
node operator * (const node &a,const node &b)
{
	node rt;rt.n=a.n,rt.m=b.m;clean(rt);
	if(a.m!=b.n) return rt;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			for(int k=1;k<=n;k++) rt.w[i][j]=(rt.w[i][j]+a.w[i][k]*b.w[k][j]%mod)%mod;
		}
	}
	return rt;
};
signed main()
{
	int k;scanf("%lld%lld",&n,&k);aa.n=n,aa.m=n;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++) scanf("%lld",&aa.w[i][j]);
	}
	node ans;init(ans,n);
	while(k)
	{
		if(k%2==1) ans=(ans*aa);
		aa=aa*aa; k>>=1;	
	}
	for(int i=1;i<=ans.n;i++)
	{
		for(int j=1;j<=ans.m;j++) printf("%lld ",ans.w[i][j]%mod);
		printf("\n");
	}
	return 0;
}

P6435 「EZEC-1」数列很细节的操作呢，对于这个序列前移操作确实没想到。

#include
using namespace std;
int n,s,m,k;
struct node
{
	int n,m,w[101][101];
	friend node operator *(const node &x,const node &y)
	{
		node rt;rt.n=x.n,rt.m=y.m;memset(rt.w,0,sizeof(rt.w));
		for(int i=1;i<=rt.n;i++)
		{
			for(int j=1;j<=rt.m;j++)
			{
				for(int k=1;k<=x.m;k++) rt.w[i][j]=(rt.w[i][j]+x.w[i][k]*y.w[k][j]);
			} 
		}
		return rt;
	};
};node ans;
void init(node &now,int x)
{
	now.n=x,now.m=x;
	for(int i=1;i<=x;i++) now.w[i][i]=1;
	return ;
}
node ksm(node x,int k)
{
	node base;init(base,n); 
	while(k)
	{
		if(k&1) base=base*x;
		x=x*x;k>>=1;
	}
	return base;
}
int main()
{
	scanf("%d%d%d%d",&n,&s,&m,&k);node x;ans.n=ans.m=n;x.n=x.m=n;
	for(int i=1;i<=n;i++) scanf("%d",&ans.w[1][i]);
	for(int i=1;i<=n;i++) x.w[1+i%n][i]=1;
	swap(x.w[s],x.w[m]);ans=ans*ksm(x,k);
	for(int i=1;i<=n;i++) printf("%d ",ans.w[1][i]);
	return 0;
} 

P2044 [NOI2012] 随机数生成器这个矩阵是我自己手推的！（虽然不是很难）但还是很厉害！

#include
#define int long long 
using namespace std;
int n,m,k,a,c,mod,g;
int gsc(int x,int y)
{
	int rt=0;(x+=mod)%mod;(y+=mod)%mod;
	while(y)
	{
		if(y&1) rt=(rt+x)%mod;
		x=(x+x)%mod;y>>=1;
	}
	return rt;
}
struct node
{
	int n,m,w[201][201];
	friend node operator *(const node &x,const node &y)
	{
		node rt;rt.n=x.n,rt.m=y.m;memset(rt.w,0,sizeof(rt.w));
		for(int i=1;i<=rt.n;i++)
		{
			for(int j=1;j<=rt.m;j++)
			{	
				for(int k=1;k<=x.m;k++) rt.w[i][j]=(rt.w[i][j]+gsc(x.w[i][k]%mod,y.w[k][j]%mod)+mod)%mod;
			}
		}
		return rt;
	}
};node ans;
void init(node &now,int x)
{
	now.m=now.n=x;	
	for(int i=1;i<=x;i++) now.w[i][i]=1;
	return ;
}
node ksm(node x,int k)
{ 
	node rt;init(rt,2);
	while(k)
	{
		if(k&1) rt=rt*x;
		x=x*x;k>>=1;
	}
	return rt;
}
signed main()
{
	scanf("%lld%lld%lld%lld%lld%lld",&mod,&a,&ans.w[1][2],&ans.w[1][1],&k,&g);
	node x;x.n=x.m=2;x.w[1][1]=a;x.w[2][1]=x.w[2][2]=1;ans.n=ans.m=2;
	ans=ans*ksm(x,k);printf("%lld",(g+ans.w[1][1])%g);
	return 0;
}

P3216 [HNOI2011]数学作业说句闲话，学习数学的最好方式就是：睡大觉。那么不妨尝试推一推每一位的式子

#include
#define int long long 
using namespace std;
int n,m,mod,t[100001];
struct node 
{
	int n,m,w[101][101];
	friend node operator *(const node &x,const node &y)
	{
		node rt;rt.n=x.n,rt.m=y.m;memset(rt.w,0,sizeof(rt.w));
		for(int i=1;i<=rt.n;i++)
		{
			for(int j=1;j<=rt.m;j++)
			{
				for(int k=1;k<=x.m;k++) rt.w[i][j]=(rt.w[i][j]+x.w[i][k]%mod*y.w[k][j]%mod)%mod;//printf("%lld\n",rt.w[i][k]);
			}
		}
		return rt;
	}; 
};node ans,c;
void init(node &now,int x)
{
	now.n=now.m=x;memset(now.w,0,sizeof(now.w));
	for(int i=1;i<=x;i++) now.w[i][i]=1;
	return ;
}
node power(node x,int k)
{
	node rt;init(rt,3);
	while(k)
	{
		if(k&1) rt=rt*x;
		x=x*x;k>>=1;
	}
	return rt;
}
signed main()
{
	scanf("%lld%lld",&n,&mod);ans.n=ans.m=c.n=c.m=3;t[0]=1;
	ans.w[1][2]=ans.w[1][3]=c.w[2][1]=c.w[2][2]=c.w[3][2]=c.w[3][3]=1;
	for(int i=1;i<=19;i++) t[i]=t[i-1]*10;
	for(int i=1;i;i++)
	{
		c.w[1][1]=t[i]%mod;int tmp=min(n,t[i]-1)-t[i-1]+1;
		ans=ans*power(c,tmp);if(t[i]-1>=n) break;
	}
	printf("%lld",ans.w[1][1]);
	return 0;
}

P1397 [NOI2013] 矩阵游戏呃这个要用费马小定理的散了吧。
那么学一学图论版？P2151 [SDOI2009] HH去散步，大概我会努力说明白的吧，欸，你有没有认真理解过矩阵的性质，你真的知道(a*b=c)的c数组如何得出来的嘛？不会的话快去看看别人的题解（https://www.luogu.com.cn/problem/solution/P2151）学一学哈哈哈哈哈。
既然你已经对矩阵的本质有了些基础的了解，不妨想一想，a矩的第一行，与b矩的第一列，与c第一个点的关系？显然，乘积和对吧，感性的看看，那么仔细一想，好像有点想法，是什么呢，不妨设f[i][j]是从i到j的路径数吧，然后你想想，它每一行枚举的是什么。形象而言f[3][1]对吧，你要走一转。

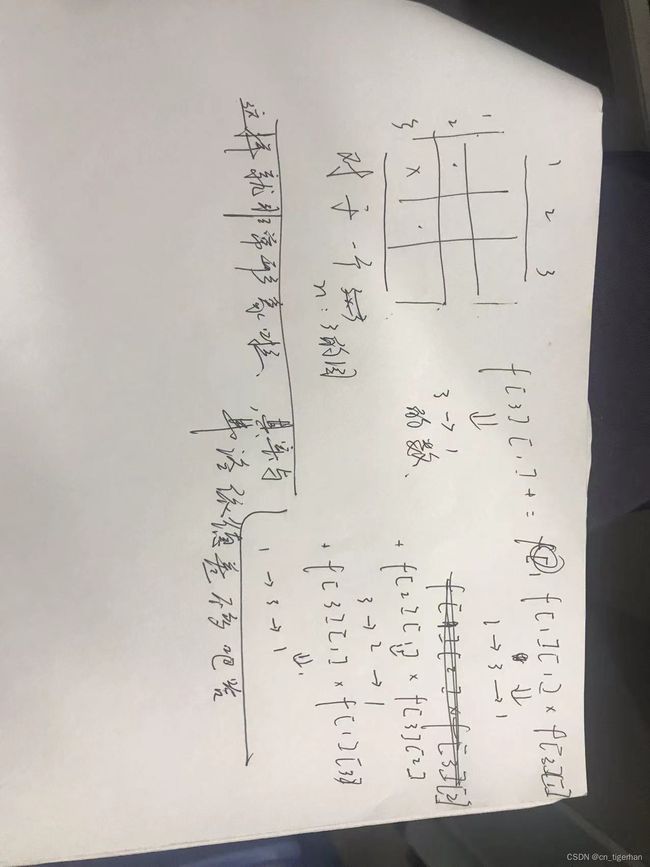
能看懂否？若不行还是算了吧qwq。理论上将其实就是枚举中转点（确实像佛洛依德），然后其他点到3的路径数是会算上的不然自己手推去，所以不用在意。
那么说回题目，我们不妨尝试理解题面：其实就是让你求有多少条长度为t的路径，但是有一个特殊条件：不能走过一条边以后又立刻反着走一次（如果两次经过同意条边中间隔了别的边是可以的），所以也许大概我们可以先用dp处理出来，然后再用矩阵加速。那么小细节dp的时候注意我们要用边，所以我们构建矩阵的时候也是用边。

#include
using namespace std;
int n,m,k,len=1,last[100001],mod=45989;
struct pp
{
	int x,y,next;
};pp p[100001];
struct node
{
	int n,m,w[250][250];
	friend node operator *(const node &x,const node &y)
	{
		node rt;rt.n=x.n,rt.m=y.m;memset(rt.w,0,sizeof(rt.w));
		for(int i=1;i<=rt.n;i++)
		{
			for(int j=1;j<=rt.m;j++)
			{
				for(int k=1;k<=x.m;k++) rt.w[i][j]=(rt.w[i][j]+x.w[i][k]*y.w[k][j]%mod)%mod;//printf("%d\n",rt.w[i][j]);
			}
		}
		return rt;
	};
};node ans,base,A,B;
void init(node &now,int x)
{
	now.n=now.m=x;memset(now.w,0,sizeof(now.w)); 
	for(int i=1;i<=x;i++) now.w[i][i]=1;
	return ;
}
void ins(int x,int y)
{
	int now=++len;
	p[now]={x,y,last[x]};last[x]=now; 
	return ;	
}
node power(node x,int k)
{
	node rt;init(rt,len);
	while(k)
	{
		if(k&1) rt=rt*x;
		x=x*x;k>>=1; 
	}
	return rt;
}
int main()
{
	memset(last,-1,sizeof(last));//printf("*");
	int ST,ED;scanf("%d%d%d%d%d",&n,&m,&k,&ST,&ED);ST++,ED++;
	for(int i=1;i<=m;i++)
	{
		int x,y;scanf("%d%d",&x,&y);x++,y++;
		ins(x,y);ins(y,x); 
	}B.n=1;B.m=A.n=A.m=len;
	for(int i=1;i<=len;i++)
	{
		int x=p[i].y;
		for(int j=last[x];j!=-1;j=p[j].next)	
		{//printf("%d %d ",i,j);
			if((i^1)==j) continue ;
			A.w[i][j]++;
		}
	}
	for(int i=last[ST];i!=-1;i=p[i].next) B.w[1][i]+=1;
	ans=B*power(A,k-1);int sum=0;
	for(int i=last[ED];i!=-1;i=p[i].next) (sum+=ans.w[1][i^1])%=mod;
	printf("%d",sum%mod);
	return 0;
}

P3758 [TJOI2017]可乐

#include
using namespace std;
int n,m,k,mod=2017;
struct pp
{
	int x,y,next;
};pp p[100001];
struct node
{
	int n,m,w[250][250];
	friend node operator *(const node &x,const node &y)
	{
		node rt;rt.n=x.n,rt.m=y.m;memset(rt.w,0,sizeof(rt.w));
		for(int i=0;i<=rt.n;i++)
		{
			for(int j=0;j<=rt.m;j++)
			{
				for(int k=0;k<=x.m;k++) rt.w[i][j]=(rt.w[i][j]+x.w[i][k]*y.w[k][j]%mod)%mod;//printf("%d\n",rt.w[i][j]);
			}
		}
		return rt;
	};
};node ans,A,B;
void init(node &now,int x)
{
	now.n=now.m=x;memset(now.w,0,sizeof(now.w)); 
	for(int i=1;i<=x;i++) now.w[i][i]=1;
	return ;
}
node power(node x,int k)
{
	node rt;init(rt,m);
	while(k)
	{
		if(k&1) rt=rt*x;
		x=x*x;k>>=1;
	}
	return rt;
}
int main()
{ 	
	scanf("%d%d",&n,&m);A.n=A.m=ans.n=ans.m=n;
	for(int i=1;i<=m;i++) 
	{
		int x,y;scanf("%d%d",&x,&y);
		A.w[x][y]=A.w[y][x]=1;
	}
	for(int i=0;i<=n;i++) A.w[i][i]=1;
	for(int i=1;i<=n;i++) A.w[i][0]=1;
	scanf("%d",&k);ans=power(A,k);int sum=0;
	for(int i=0;i<=n;i++) (sum+=ans.w[1][i])%=mod;
	printf("%d",sum);
	return 0;  
}

P2886 [USACO07NOV]Cow Relays G矩阵优化弗洛伊德这这这，很高级的样子

#include
using namespace std;
int n,m,id[2000001],tot=0;
struct pp
{
	int x,y,next;
};pp p[2000001];
struct node
{
	int n,m,w[200][200];
	friend node operator *(const node &x,const node &y)
	{
		node rt;rt.n=x.n,rt.m=y.m;memset(rt.w,63,sizeof(rt.w));
		for(int i=1;i<=rt.n;i++)
		{
			for(int j=1;j<=rt.m;j++)
			{
				for(int k=1;k<=x.m;k++) rt.w[i][j]=min(rt.w[i][j],x.w[i][k]+y.w[k][j]);//printf("%d\n",rt.w[i][j]);
			}
		}
		return rt;
	};
};node ans,A,B;
node power(node x,int k)
{
	node rt=x;k--;
	while(k)
	{
		if(k&1) rt=rt*x;
		x=x*x;k>>=1;
	}
	return rt;
}
int main()
{
	memset(A.w,63,sizeof(A.w));memset(id,0,sizeof(id));
	int k,ST,ED;scanf("%d%d%d%d",&k,&m,&ST,&ED);
	for(int i=1;i<=m;i++)
	{
		int x,y,c;scanf("%d%d%d",&c,&x,&y);
		if(!id[x]) id[x]=++tot;
		if(!id[y]) id[y]=++tot;
		A.w[id[x]][id[y]]=A.w[id[y]][id[x]]=min(A.w[id[x]][id[y]],c);
	}
	A.n=A.m=tot+1;ans=power(A,k);
	printf("%d",ans.w[id[ST]][id[ED]]); 
	return 0;
}

介绍一个矩阵+拆点的：P4159 [SCOI2009] 迷路

#include
using namespace std;
int n,m,k,mod=2009;
struct node
{
	int n,m,w[101][101];
	friend node operator *(const node &x,const node &y)
	{
		node rt;rt.n=x.n,rt.m=y.m;memset(rt.w,0,sizeof(rt.w));
		for(int i=1;i<=rt.n;i++)
		{
			for(int j=1;j<=rt.m;j++)
			{
				for(int k=1;k<=x.m;k++) rt.w[i][j]=(rt.w[i][j]+x.w[i][k]*y.w[k][j])%mod;//printf("%d",rt.w[i][j]);
			}
		}
		return rt;
	};
};node ans,A;
void init(node &now,int x)
{
	now.n=now.m=x;memset(now.w,0,sizeof(now.w));
	for(int i=1;i<=x;i++) now.w[i][i]=1;
	return ;
}
node power(node x,int k)
{
	node rt;init(rt,m); 
	while(k)
	{
		if(k&1) rt=rt*x;
		x=x*x;k>>=1;
	}
	return rt;
}
inline int getpos(const int &u, const int &i)
{
	return u + i * n; 
}
int main()
{
	scanf("%d%d",&n,&k);m=n*9;A.n=A.m=m;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=8;j++) A.w[getpos(i,j)][getpos(i,j-1)]=1;
		for(int j=1;j<=n;j++)
		{
			int x;scanf("%1d",&x); 
			if(x) A.w[i][getpos(j,x-1)]=1;
		}
	} 
	ans=power(A,k);printf("%d",ans.w[1][n]);
	return 0;
 } 

P5678 [GZOI2017]河神麻烦了些，不写QWQ
P4838 P哥破解密码，好的转移思路。

//考虑dp，令f[i][j]为在第i位向左有多少个连续的A（j<=2	）这样近乎O(n)的转移，不够。
//考虑优化，发现:
//	f[i][0]=f[i-1][0]+f[i-1][1]+f[i-1][2];
//	f[i][1]=f[i-1][0];
//	f[i][2]=f[i-1][1];(其实也可以看作f[i-2][0]) 
//那么转移式推出来之后发现可以尝试矩阵优化一下，令f[1][0]=f[1][1]=1,f[1][2]=0;
//答案明显，考虑转移。这简单的一匹！推推推！ 
//	
#include
#define int long long 
using namespace std;
int n,m,k,mod=19260817;
struct node
{
	int n,m,w[101][101];	
	friend node operator *(const node &x,const node &y)
	{
		node rt;rt.n=x.n,rt.m=y.m;memset(rt.w,0,sizeof(rt.w));
		for(int i=1;i<=rt.n;i++)
		{
			for(int j=1;j<=rt.m;j++)
			{
				for(int k=1;k<=x.m;k++) rt.w[i][j]=(rt.w[i][j]+x.w[i][k]*y.w[k][j])%mod;
			}
		}
		return rt;
	};
};node ans,A,B;
void init(node &now,int x)
{
	now.n=now.m=x;memset(now.w,0,sizeof(now.w));
	for(int i=1;i<=x;i++) now.w[i][i]=1;
	return ;
}
node power(node x,int k)
{
	node rt;init(rt,3);
	while(k)
	{
		if(k&1) rt=rt*x;
		x=x*x;k>>=1;	
	}
	return rt;
}
main()
{
	A.n=A.m=3;A.w[1][3]=A.w[2][1]=A.w[2][3]=A.w[3][2]=A.w[3][3]=1;
	A.w[1][1]=A.w[1][2]=A.w[2][2]=A.w[3][1]=0;B.n=B.m=3;B.w[1][3]=1;	
	int t;scanf("%lld",&t);
	while(t--)
	{
		scanf("%lld",&n);ans=B*power(A,n);
		printf("%lld\n",(ans.w[1][1]+ans.w[1][2]+ans.w[1][3])%mod);
	}
	return 0;
}