多用户MIMO系统（八）：基于用户服务质量（QoS）的设计、SDP/SDR的Matlab实现

多用户MIMO系统（八）：基于用户服务质量（QoS）的设计

关键词

MIMO，多用户，用户QoS，半正定规划，半正定松弛，Matlab实现

基本介绍

本文介绍了多用户MIMO系统基于用户QoS的预编码设计，优化目标为在保证每个用户QoS的前提下最小化基站传输功率。通过引入辅助变量，发现这一优化问题可以采用半正定规划以及半正定松弛来解决，并且给出了对应的Matlab实现。

主要内容

考虑图1所示下行多用户MIMO系统，基站配置多条天线，天线数为$N$，用户均配置多天线，用户数为$K$。此处从保证用户服务质量（quality of service, QoS）的角度对发射端预编码以及功率分配策略进行设计。具体来讲，用户$k$收到的信号为：$$y_k={\text{h}}_k^{†}{\text{w}}_k{s}_k+\sum _{j\ne k}{\text{h}}_k^{†}{\text{w}}_j{s}_j+n_k,$$其中$n_k\sim \mathcal{C}\mathcal{N}\left(0,{\sigma }_k^2\right)$表示用户侧加性白高斯噪声，${\sigma }_k^2$为噪声功率，$s_k\in \mathbb{C}$是基站传给用户$k$的信号，满足$\mathbb{E}\left\{s_k{s}_k^{†}\right\}=1$，${\text{w}}_k\in {\mathbb{C}}^{N\times 1}$表示用户$k$的预编码向量，${\text{h}}_k\in {\mathbb{C}}^{N\times 1}$表示基站与用户$k$的之间的信道。对于用户$k$而言，信干噪比为${\gamma }_k=\frac{{|{\text{h}}_k^{†}{\text{w}}_k|}^2}{{\sum }_{j\ne k}{|{\text{h}}_k^{†}{\text{w}}_j|}^2+{\sigma }_k^2}.$

图1：下行传输模型，一个基站服务多个用户。

此处预编码设计的策略为保证每个用户的QoS，即使得每个用户的信干噪比大于某个预设值${\bar{\gamma }}_k$，同时使得总的传输功率${\sum }_{k=1}^K\left|{\text{w}}_k^{†}{\text{w}}_k\right|$最小。问题建模为：[1]$$\begin{array}{rl}\underset{\left\{{\text{w}}_i\right\}}{\min }& \sum _{k=1}^K\left|{\text{w}}_k^{†}{\text{w}}_k\right|\\ \text{s.t.}& {\gamma }_k=\frac{{\left|{\text{h}}_k^{†}{\text{w}}_k\right|}^2}{{\sum }_{j\ne k}{\left|{\text{h}}_k^{†}{\text{w}}_j\right|}^2+{\sigma }_k^2}\ge {\bar{\gamma }}_k,\forall k.\end{array}$$上述问题可以采用半正定规划（Semidefinite programming，SDP）来解决[2]。定义${\text{W}}_k={\text{w}}_k{\text{w}}_k^{†}$，可知${\text{W}}_k⪰\text{0}$是个半正定矩阵，且${\text{W}}_k$的秩$\text{rank}\left({\text{W}}_k\right)$为1，即$\text{rank}\left({\text{W}}_k\right)=1$。此外，定义${\text{H}}_k={\text{h}}_k{\text{h}}_k^{†}$，则信干噪比可以写为：$${\gamma }_k=\frac{{\left|{\text{h}}_k^{†}{\text{w}}_k\right|}^2}{{\sum }_{j\ne k}{\left|{\text{h}}_k^{†}{\text{w}}_j\right|}^2+{\sigma }_k^2}=\frac{{\text{w}}_k^{†}{\text{h}}_k{\text{h}}_k^{†}{\text{w}}_k}{{\sum }_{j\ne k}{\text{w}}_j^{†}{\text{h}}_k{\text{h}}_k^{†}{\text{w}}_j+{\sigma }_k^2}=\frac{\text{Tr}\left({\text{W}}_k{\text{H}}_k\right)}{{\sum }_{j\ne k}\text{Tr}\left({\text{W}}_j{\text{H}}_k\right)+{\sigma }_k^2},$$上述问题可以等价地写为：$$\begin{array}{rl}\underset{\left\{{\text{w}}_i\right\}}{\min }& \sum _{k=1}^K\text{Tr}\left({\text{W}}_k\right)\\ \text{s.t.}& {\bar{\gamma }}_k\sum _{j\ne k}\text{Tr}\left({\text{W}}_j{\text{H}}_k\right)+{\bar{\gamma }}_k{\sigma }_k^2-\text{Tr}\left({\text{W}}_k{\text{H}}_k\right)\le 0,\forall k,\\ & {\text{W}}_k⪰\text{0},\forall k,\\ & \text{rank}\left({\text{W}}_k\right)=1,\forall k.\end{array}$$如果将上述问题中的制约条件“$\text{rank}\left({\text{W}}_k\right)=1$”给去掉，那么这个问题就是一个标准的凸优化问题，可以用CVX工具包直接求解[3]。由于优化变量都是半正定矩阵，这个问题也被称为半正定规划问题。因为这是个凸问题，所以CVX工具包可以直接求出它的最优解，但需要注意的是上述问题没有考虑$\text{rank}\left({\text{W}}_k\right)=1$这一约束条件，因此这只是原问题的一个次优解。不过，幸运的是，利用KKT条件，可以推导得出上述问题的解一定满足$\text{rank}\left({\text{W}}_k\right)=1$这个约束条件[4]。也就是说，通过求解下述松弛问题：
$$\begin{array}{rl}\underset{\left\{{\text{w}}_i\right\}}{\min }& \sum _{k=1}^K\text{Tr}\left({\text{W}}_k\right)\\ \text{s.t.}& {\bar{\gamma }}_k\sum _{j\ne k}\text{Tr}\left({\text{W}}_j{\text{H}}_k\right)+{\bar{\gamma }}_k{\sigma }_k^2-\text{Tr}\left({\text{W}}_k{\text{H}}_k\right)\le 0,\forall k,\\ & {\text{W}}_k⪰\text{0},\forall k,\end{array}$$ 可以获得原问题的最优解。

以下，给出具体的Matlab代码来解决上述半正定规划问题。

QoS_Signal_to_Noise_Ratio = [-5:5:25]; % 用户QoS，用信噪比表示，单位为dB
Monte_Carlo = 2000; % 蒙特卡洛仿真次数
N = 4; % 基站天线数
K = 4; % 用户数
noise = 1; % 噪声功率为0 dB
Data = ones(Monte_Carlo,length(QoS_Signal_to_Noise_Ratio));
for Monte = [1:1:Monte_Carlo]
    Tmp_Data = ones(1,length(QoS_Signal_to_Noise_Ratio));
    for QoS_index = [1:1:length(QoS_Signal_to_Noise_Ratio)]
        [Monte,QoS_index]
        snr = 10^(QoS_Signal_to_Noise_Ratio(QoS_index)/10);
        H = 1/sqrt(2)*randn(K,N) + 1j*1/sqrt(2)*randn(K,N); % MIMO信道(考虑瑞利衰落模型)
        A = ones(N,N,K); % 存储用户信道与其自身的共轭转置的乘积，即h_k*(h_k)^{H}
        for index = [1:1:K]
            A(:,:,index) = H(index,:)' * H(index,:);
        end      
        Tmp_Data(QoS_index) = CVX_QoS_SDP(A,N,snr,noise); % 利用CVX求解SDP问题
    end
    Data(Monte,:) = Tmp_Data;
end
%% 注意由于SDP问题采用CVX工具包进行数值求解，容易发生数据溢出的现象，
%  此外，由于精度等的设置，仿真出来的数据未必都是有效的数据。因此，我们
%  需要从获取的全部数据中筛选出合理的数据。此处采用的筛选办法叙述如下：
%  直观来看，用户QoS信噪比越高，所需的传输功率越大，利用这条规律，我们筛
%  选出2000条数据中，传输功率随用户QoS信噪比单调递增的数据用于绘图。
Tmp = []; % 存储筛选后的数据
for i=1:size(Data,1)
    if Data(i,:)==sort(Data(i,:)) % 判断当前数据里传输功率是否随用户QoS信噪比单调递增
        Tmp = [Tmp;Data(i,:)]; % 只留下传输功率随用户QoS信噪比单调递增的数据
    end
end
plot(QoS_Signal_to_Noise_Ratio,mean(10*log10(Tmp)),'-v');
xlabel('用户QoS [dB]');
ylabel('传输功率 [dB]');
grid on;

其中，函数CVX_QoS_SDP通过利用CVX求解SDP问题。

function [y] = CVX_QoS_SDP(A,Antenna_Number,QoS,noise)
% CVX_QoS_SDP 利用半正定规划求解MU-MISO系统保证用户QoS的预编码设计问题
% Antenna_Number 表示基站天线数
% A 存储了信道矩阵
% QoS 存储了用户QoS信噪比
% noise 存储了噪声功率
N = Antenna_Number;
snr = QoS;
cvx_clear
cvx_begin quiet
% 定义变量，一共有4个，它们都是复数半正定矩阵（complex semidefinite）
variable X1(N,N) complex semidefinite
variable X2(N,N) complex semidefinite
variable X3(N,N) complex semidefinite 
variable X4(N,N) complex semidefinite
minimize(real(trace(X1)+trace(X2)+trace(X3)+trace(X4))); % 目标函数
% 注意由于优化变量为复数，尽管目标函数的虚部为0，也需要取目标函数的实部，以保证程序不出错
% 上述注意事项也可用于制约条件
subject to % 以下为各个用户的QoS制约条件，A(:,:,i)存储了用户信道与其自身的共轭转置的乘积，即h_k*(h_k)^{H}
snr*real(trace(A(:,:,1)*X2) + trace(A(:,:,1)*X3) + trace(A(:,:,1)*X4) + noise) - real(trace(A(:,:,1)*X1)) <= 0;
snr*real(trace(A(:,:,2)*X1) + trace(A(:,:,2)*X3) + trace(A(:,:,2)*X4) + noise) - real(trace(A(:,:,2)*X2)) <= 0;
snr*real(trace(A(:,:,3)*X1) + trace(A(:,:,3)*X2) + trace(A(:,:,3)*X4) + noise) - real(trace(A(:,:,3)*X3)) <= 0;
snr*real(trace(A(:,:,4)*X1) + trace(A(:,:,4)*X2) + trace(A(:,:,4)*X3) + noise) - real(trace(A(:,:,4)*X4)) <= 0;
cvx_end
y = real(trace(X1)+trace(X2)+trace(X3)+trace(X4)); % 返回优化后的目标函数值
end

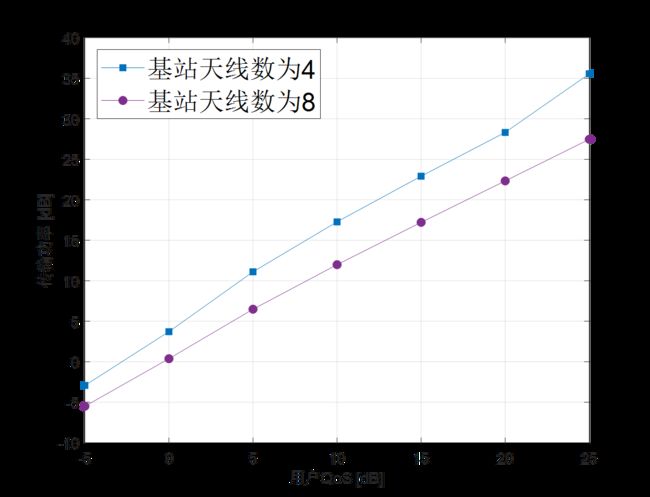图2.8.2：基站传输功率与用户QoS信噪比的关系，信道采用瑞利衰落模型，蒙特卡洛仿真次数设置为2000，$K=4$，${\sigma }^2=1$。

图2绘制了基站传输功率随用户QoS信噪比变化的曲线，从图中可以看出，增加基站天线数可以降低用户传输功率。注意，此处每个用户的QoS信噪比设置为相同取值。

参考文献

1. E. Karipidis, N. D. Sidiropoulos, and Z.-Q. Luo, ‘‘Quality of service and max-min fair transmit beamforming to multiple cochannel multicast groups,’’ IEEE Trans. Signal Process., vol. 56, no. 3, pp. 1268–1279, Mar. 2008.
2. Z. Luo, W. Ma, A. M. So, Y. Ye, and S. Zhang, “Semidefinite relaxation of quadratic optimization problems,” IEEE Signal Process. Mag., vol. 27, no. 3, pp. 20–34, 2010.
3. S. Boyd and L. Vandenberghe, Convex Optimization. Cambridge, U.K.: Cambridge Univ. Press, 2004.
4. C.-Y. Chi, W.-C. Li, and C.-H. Lin, Convex Optimization for Signal Processing and Communications: From Fundamentals to Applications. Boca Raton, FL, USA: CRC Press, 2017.