100篇文献-万字总结 || 强化学习求解车间调度

获取更多资讯，赶快关注上面的公众号吧！

近年来强化学习和深度强化学习不断用于求解调度问题，其是在动态调度问题上，它们可以根据不同的调度状态获得自适应的调度策略，在遇到新的问题时，只需要输入新的调度特征就可以快速获得调度解，而无需重新训练。

本文中，作者就强化学习和深度强化学习在生产调度中的应用进行了较为全面的综述，旨在为生产调度从业者和对生产调度应用感兴趣的深度强化学习研究者提供参考。

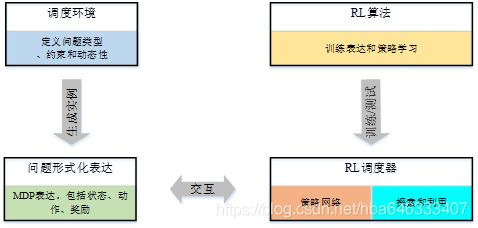
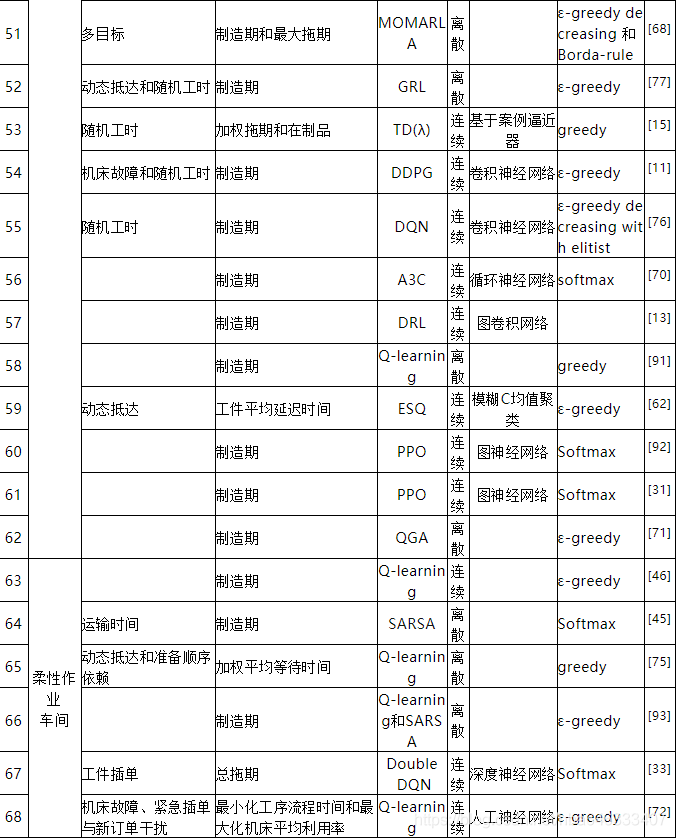
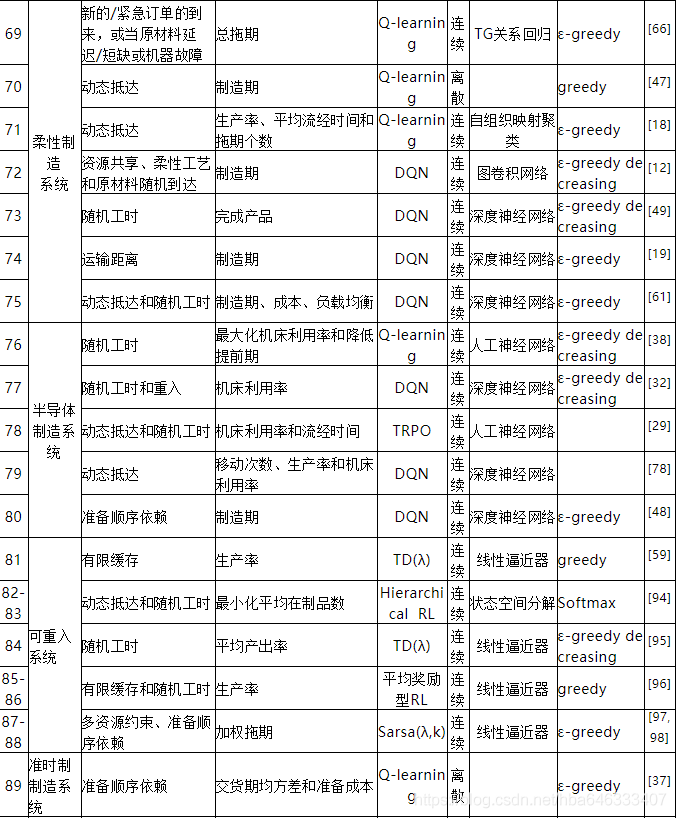
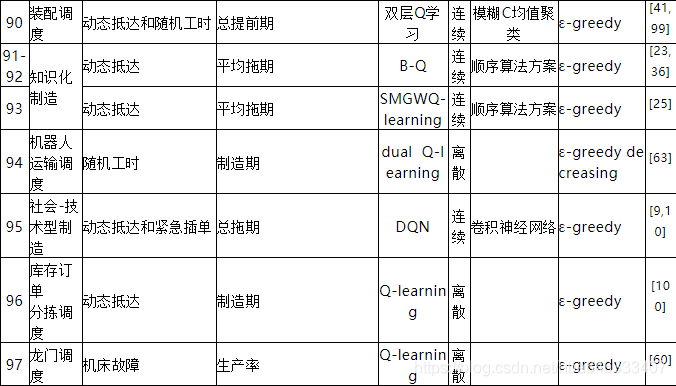
  强化学习求解生产调度问题最早可追溯于1995年[1]，自此国内外学者竞相开始研究，并且随着深度强化学习的迅猛发展，近年来其在调度中的应用呈上升趋势。本研究对97篇相关文献进行了仔细研究，从中提炼出了强化学习求解车间调度问题的一般过程，如图1所示。调度环境定义了问题类型、约束和动态性，并由此生成调度实例，根据状态、动作和奖励将实例表达为MDP。强化学习调度器不断与MDP交互获得数据样本，强化学习算法进行训练表达和策略学习，为了适用于大规模问题，需要通过策略网络来参数化策略，平衡探索和利用可以保证调度器在合理的时间内收敛到最优解。

图1 RL求解车间调度的一般过程

  本文将根据以上过程，分别从强化学习的基本组成元素——状态、动作、奖励、探索和利用策略等方面综述使用RL求解车间调度问题时的应用情况。

状态

  状态用于描述系统环境的本质特征，包括整体特征和局部特征。状态空间是所有可能的状态所组成的集合。把智能体需要作出决策的状态称为决策状态。强化学习算法对值函数的评估是建立在对状态或行为的多次重复地基础上，对于小规模状态空间问题，可以用列显式表示每一个状态或行为的值。但实际问题往往具有大规模或连续的状态空间，强化学习算法不可能遍历所有状态，很多状态不具有重复性，因此强化学习算法将面临“维数灾难”问题[2]，在这种情况下，状态或动作的值不能用列表显式表示。解决该问题的方法主要有两类：一类是基于离散化的方法，把连续状态空间离散化，或者把大规模空间通过压缩、分解等手段转化为小规模状态空间，增大状态空间划分的粒度，在减小问题规模、分解状态空间的同时尽可能保持原有问题的结构与性质；另一类是值函数泛化（值函数逼近）方法。值函数泛化是一种降维处理的方法，它根据经历过的状态或行为值推测尚未经历过的状态或动作值，从而得到这些状态或行为值的近似表示，而近似表示最重要的基础是选取合适的特征，所以本节内容主要说明可以用来描述调度系统的特征属性，并由此构造用于强化学习的状态特征。

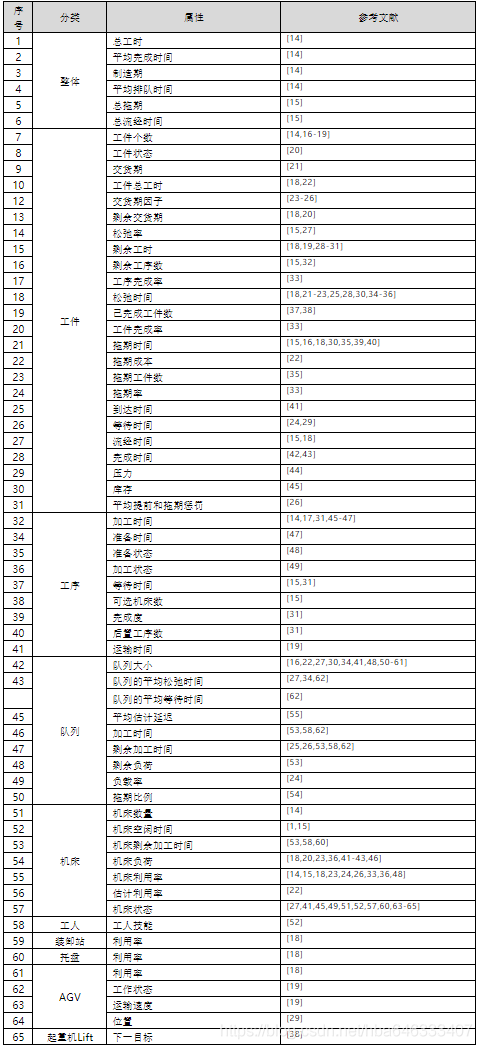
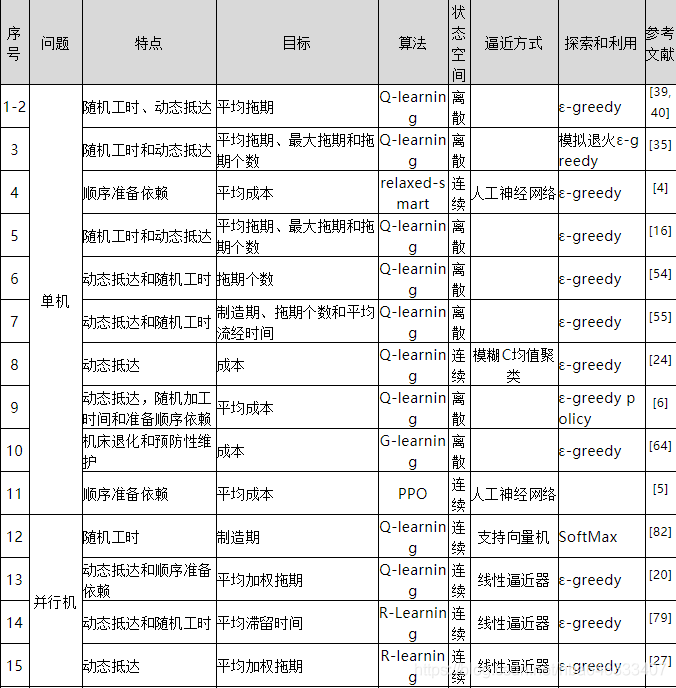
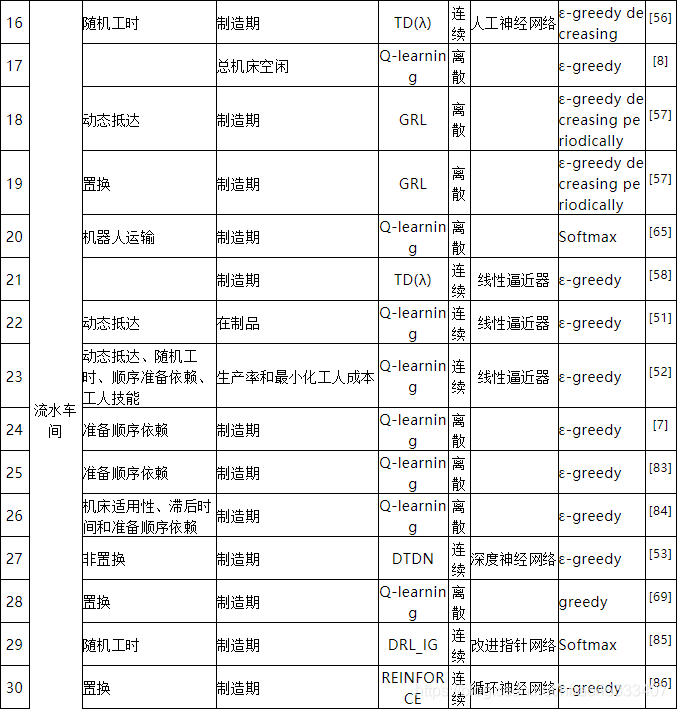
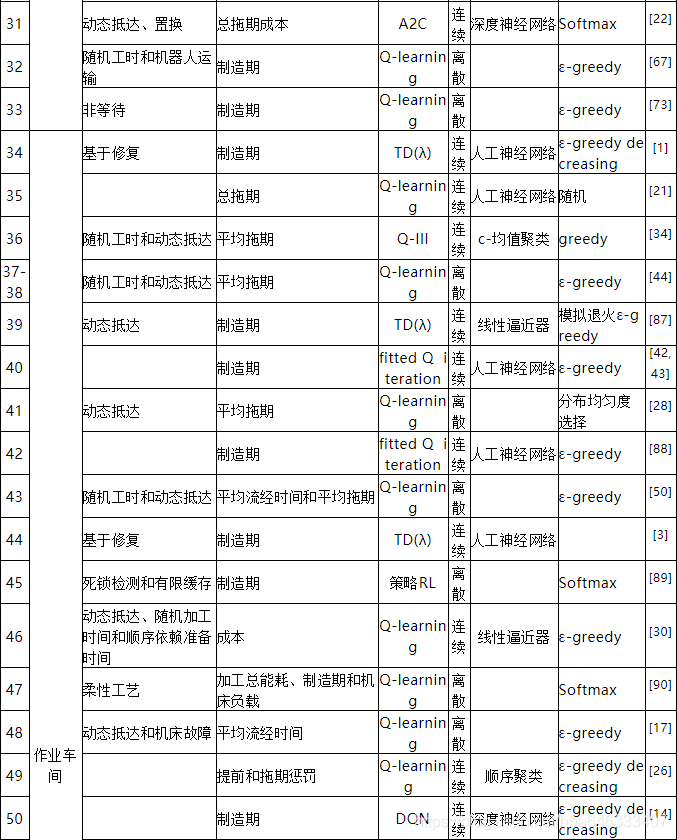
  简单启发式规则往往只根据单一属性作为排序的依据，如SPT（Shortest ProcessingTime）规则根据加工工时进行排序，工时越短越优先分派，而加权优先级的思想是利用多个和工件相关的属性来确定调度顺序，每项属性都分配了权重以表示其相对重要性，一般情况下得到的调度结果要优于单一简单规则，简单规则的短视性主要是由仅仅考虑了局部信息导致的，针对不同调度案例调度性能差异很大。大多数强化学习解决调度问题的目的是建立多个调度属性和目标之间的关系，使不同的动作可以自适应地选择。表1列出了目前在强化学习求解调度问题文献中用于帮助设计调度状态的不同类型的调度特征属性。注意，文章中可能并不是直接使用该属性值构成状态特征，而是执行了标准化等其他处理以增加泛化性。

  除了使用这些调度属性作为特征以外，不同的调度方法还可以使用不同形式的状态定义。例如，在基于修复的调度中，Williem和Zhang[1,3]使用从调度中抽取的特征向量来表示关键路径调度；在考虑切换时间的调度[4-6]中，第m个决策代时的系统状态可以表达为，其中为第i个产品的库存状态，Mm表示机床当前正在准备的产品；在求解流水车间调度问题时，Stefan和FONSECA-REYNA[7,8]直接将状态定义为工件顺序，更准确地说是工件优先关系；Palombarini & Martinez[9,10]采用和DQN类似的状态表达方式，直接将一幅完整的调度甘特图作为状态；Liu等[11]也采用了类似于图像RGB通道的状态表示法，三个通道分别对应于加工时间矩阵、工件是否分派到机床的布尔矩阵和工件是否完成的布尔矩阵，这三个矩阵将作为CNN的输入；Hu等[12]使用Petri网对FMS进行建模，Petri网中的库所（place）表示条件、资源等待队列等，其包含一定数量的托肯（token），托肯在库所里的分布代表Petri网的状态即标记（marking），因此所有托肯特征就构成了RL的系统特征；Seito & Munakata[13]使用图结构表示调度，图中每个节点的值可通过图卷积神经网络提取到，在调度图结构中，可以将数值信息表示为节点属性值，而将非数值信息表示为边。

表1 强化学习调度特征属性

动作

  动作是在某个决策状态下可以采取的行为，动作空间是在每个决策状态下所有可以选择的动作所构成的集合。在调度问题中，动作一般是指通过一定的方式确定下一个需要加工的工件。针对不同的调度问题和调度应用，这种方式也有不同。

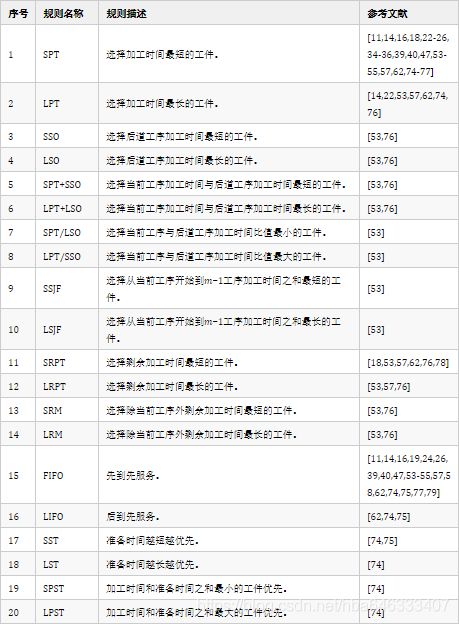
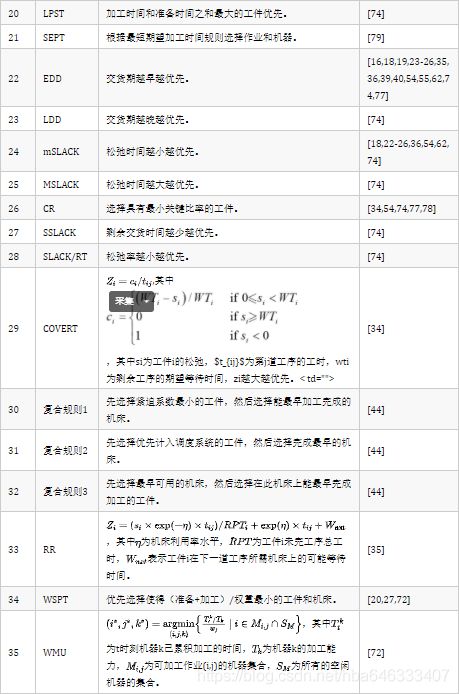
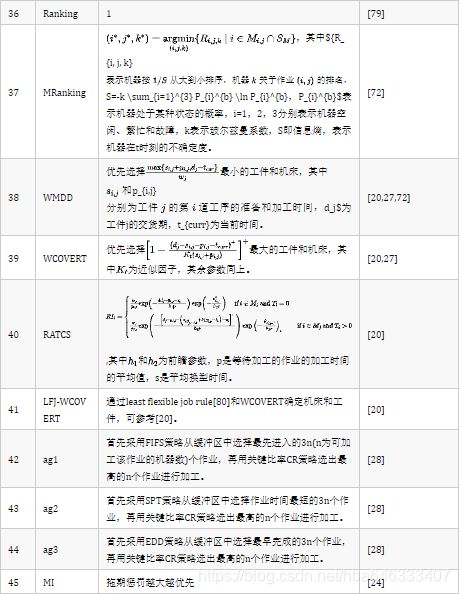
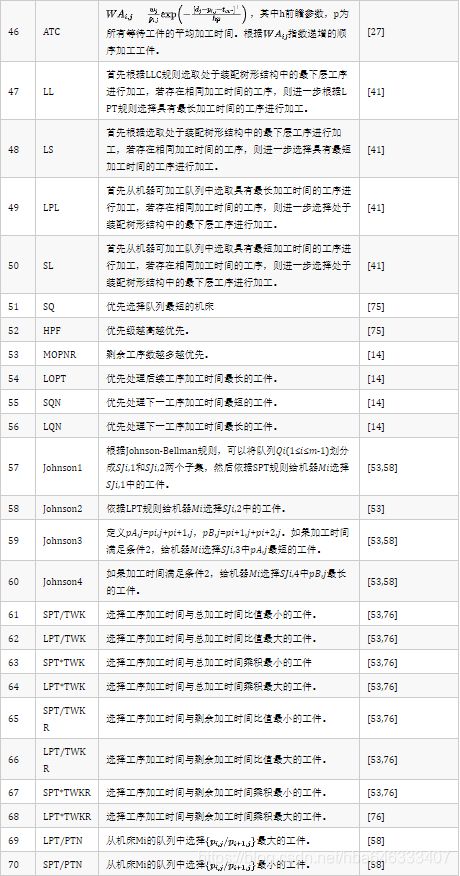
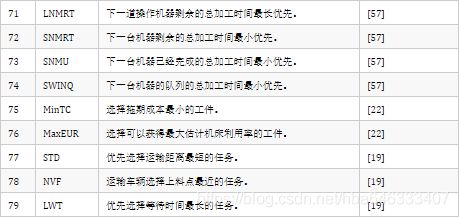
  目前大多数强化学习求解调度都是选择启发式规则，通过选择的规则对工件或机床进行排序，然后得到调度。表2中列举了在调度中应用的启发式规则。

  除了启发式规则，在不同调度问题中，还可以有不同形式的动作。在修复调度中，动作是通过操作一些工序来调整调度方案，从而消除违反的约束，如重新分派资源算子（Reassign-Pool operator）和移动算子（Move operator）[1]；Miyashita[15]以及Palombarini和Martínez[66]指定工序为修复目标，并提出10种调度修复算子外加1个空闲动作算子，这10个算子分别为slide_left、jump_left jump_alt_left、swap_left、swap_alt_left、slide_ right、jump_ right、jump_alt_ right、swap_ right和swap_alt_right。这些算子单独作用于目标工序上，但是由于调度中紧密的约束交互所产生的涟漪效应，其他工序的位置也会被移动；之后，Palombarini和Martinez[9,10]又定义了14种不同的移动，在甘特图上直接对可行解进行调整，包括Left Move、Right Move、Left Jump、Right Jump、UpLeftJump、UpRightJump、DownLeftJump、DownRightJump、UpLeftSwap、UpRightSwap、DownLeftSwap、DownRightSwap、LeftSwap和RightSwap。

  在考虑运输的调度问题中，动作是将工序分配给站点或资源[45]；Kuhnle等[29]研究的半导体制造系统也采用了类似的动作，运输资源通过在上料口、出料口和机床之间不断移动，将订单运输到不同位置；Shi等[49]将动作定义为运输完成的产品到下一工序（或加工单元）；Arviv[63]、Stern[65]和Lee[67]中的动作则表示机器人将机床Mi出缓存中的工件运输至下一机床Mi+1的入缓存；Stricker等[38]同样定义了12个动作用于确定批次的位置；Ou等[60]将龙门工作单元调度的动作定义为在某一时刻分配龙门给机床。

  杨宏兵等[64]由于考虑了机床的预测性维护，除了需要选择某种工件类型进行加工外，是否进行预防性维护也可看作是一个动作。

  还有生成调度方案更为直接的方式，就是从在队列中等待的工件中选择一个进行加工[21,37,42,43,56,57,68,69]，或从一种产品类型转换成另一种类型[4-6,30,32,48,51,52]，这种动作空间一般都会有一个不作为的动作，即保持机床空闲；在LSTM网络中，Ren等[70]引入指针网络指向当前状态下具有最高优先级的工件，从而根据输入的一组工件创建工件排序；Park等[31]使用图神经网络直接从图中选择一个目标机床可以加工的节点（工序）。

  当然也有间接的方式，这些方式通常是使用强化学习优化其他算法的参数来间接的优化调度，如选择合适的权重来构造复合规则，因此动作代表了权重向量，动作的执行意味着使用指定的权重向量来构造复合规则对工件进行排序[50]；Shahrabi等[17]则利用强化学习在重调度时刻更新变邻域搜索的参数，而不是直接优化调度。这些参数包括迭代次数N，局部搜索次数qmax和接受水平dr；Li等[71]将遗传算法的基因空间视为Q学习的动作策略空间，适应度函数为奖励函数，从而将遗传算法问题转化为强化学习问题；陈勇等[72]使用强化学习算法来探索元胞机模型中最优的自组织演化规则，通过代理的决策行为控制粒子的移动，从而逐步选择工位和工序；Zhao等[73]采用基于强化学习的水波优化算法求解非空闲流水车间调度问题，使用Q学习决定新生成水波的位置，并平衡水波传播过程的探索和利用。

表2 强化学习中使用的启发式规则

奖励

  当确定了强化学习所赖以生存的环境，学习器将学习到的行为作用于该环境，在模型的驱动下，调度系统将变迁至下一个状态，同时给出即时的奖励作为对刚才已执行行为的短期评价，奖励函数的定义与调度求解目标紧密相关。强化学习通过接收环境的奖励反馈，不断修正自身选择行为的策略，因此奖励函数的定义从本质上反映了调度优化目标，由于强化学习是最大化长期的累积奖励，因此对于最小化的目标可以采取取相反数的方法。注意奖励是一个标量值，用于导引策略优化。通过总结调度问题中的奖励函数设计方式，可以发现主要可以分为两种方法：启发式奖励和等价奖励。

  启发式奖励方法是通过一些规则去设计奖励函数，使得累积奖励增大的方向与优化的目标保持一致，但两者不一定等价，常以分段函数的形式定义，因此无法保证使用最大化累积奖励的策略可以得到最优的调度结果。Wang和Usher[40]认为一旦发生拖期，就给予一个惩罚，并且拖期越大惩罚越大，只有当没有拖期时才设置一个奖励。Kong和Wu[35]针对最小化平均拖期、最小化最大拖期和最小化拖期工件个数，分别设计了3种基于实际拖期进行分段的启发式奖励函数。此外，还可以将与调度目标相关的变量赋值在奖励函数中，如Ou等[60]为最大化系统输出，在奖励函数种考虑了瞬时生产损失和生产损失风险。这种设计方法通常需要对调度问题有足够的先验知识，奖励好的动作，惩罚差的动作，有利于算法快速收敛，但无法保证学习到最优策略。

  等价奖励则是保证最大化累积奖励等价于目标最优化，根据学习算法不同，奖励设置方法也有所不同。基于值函数的RL算法可以在片段结束时给出一个与调度相关的总奖励值[21]，而在片段结束前的其他时间步上都设置瞬时奖励为0，这种设计方式虽然简单，但是会造成稀疏奖励，导致学习速度慢甚至不能收敛；也可以采用时序差分方法在每一步都设计一个非零奖励值，然后保证累积奖励对应于调度目标，这种等价性一般需要给出数学证明。如Zhang等[27]设计了一种奖励函数，证明了最大化其无限时间内的平均时间值等同于最小化平均加权拖期。基于策略的REINFORCE可以直接使用策略最终的调度目标作为奖励，并根据该策略的对数导数进行策略梯度的计算[70]。

探索和利用

  权衡“探索”（Exploration）和“利用”（Exploitation）是应用强化学习算法要解决的一个重要问题。“探索”是指选择非当前最优的行为，探索新的行为（采取以前没有执行过的行为），“探索”有可能提升该行为的值，从而发现更好的行为，从长远来看可能获得更多的回报；“利用”是指选择当前最优的行为，这样可以充分利用已经学习到的经验知识，短期内可得到较多的奖励。过多的探索可能会削弱算法的效率和效果，而过度利用可能会导致陷入局部最优。平衡“利用”和“探索”的常用方法[132]有贪婪方法、ε-贪婪方法、ε-递减策略、Softmax等。

  贪婪方法通常选择最优行为，在Q学习中就是具有最大状态-行为值的行为，该方法的缺点是有可能陷入局部最优值。

  ε-贪婪方法以概率1-ε选择最优行为，而以概率ε随机选择，该方法可以跳出局部最优而找到最大长期回报，并可以控制对“利用”和“探索”的偏好程度：ε越大，模型具有更大的灵活性，能更快地探索潜在高回报的行为，收敛速度更快；ε越小，模型具有更好的稳定性，有更多的机会开发利用当前最好回报的行为，收敛速度变慢。虽然ε-贪婪方法算法在“探索”和“利用”之间做出了一定平衡，但设置最好的ε比较困难，大则适应变化较快，但长期累积回报低，小则适应变好的能力不够，但能获取更好的长期回报。

  对ε-贪婪方法的一种变体就是ε-递减策略（ε-decreasing strategy），ε随着时间的推移逐步降低，初始时更多地进行探索，后续选择行为时更多的是利用，当ε减少到0时则变为贪婪算法，完全选择最优行为。

  ε-递减策略虽然有很多的好处，但是一个缺点就是在探索的时候，选择每个行为的概率是一样的，也就是说很可能会选到一个最差的行为。SoftMax动作选择就是基于对这种情况的考虑，在探索的时候，还是给贪婪最大的概率，其他的行为根据其值的大小，按概率进行选择。也就是说，最差的行为被选到的概率是最小的。其计算公式如下所示：

  其中是选择行为的概率，为在状态下的可选行为的数量，为温度值。如果处于较高的温度，选择不同行为的概率相近，行为选择具有随机性，当趋于无穷时，行为选择的概率分布收敛于均匀分布，因此更高的温度下将探索新的行为；如果温度低则以更确定性的概率选择当前平均回报最好的行为。随着训练的进行，温度不断下降，因此该策略也被称为基于模拟退火的ε-贪婪策略。

  潘燕春等[57]采用了贪婪率周期性递减的策略，如式(1.7)所示，和分别为最大贪婪率和最小贪婪率，k和d分别为当前迭代次数和迭代次数基准。贪婪率ε∈[0,1]越小算法越贪婪，越能充分利用现有的学习成果；ε越大算法越随机，越有利于探索新的有效策略。该策略使得ε周期性地降低，算法可以在在任何阶段都进行探索和利用，更有可能跳出局部最优，从而在深度搜索和广度搜索中找到一个比较好的均衡。

  Wang等[6]认为在学习初期没有动作选择的知识，因为存储奖励值的矩阵被初始化为一个全零矩阵，所以他们引入了启发式方法来提升学习过程。启发式函数定义如下：

  其中为在状态时采用的策略，为实数变量（如0.1），用于衡量启发式的影响，为在[0,1]内的均匀随机数，是从所有可能的动作集中随机选择的动作。启发式函数的计算公式[81]如下：

  其中为很小的值（如0.01），为在状态下启发式所确定的动作。

结论

  强化学习算法基于状态或行为值直接面向长期目标进行学习和决策，它不需要学习环境的完整数学模型，可以从以前解决过的实例或仿真实验中学习并积累经验，通过与环境的交互过程来学习策略。它不像监督学习那样需要精确地学习目标，也无需监督和教导，而是通过采取不同的行为并利用环境的反馈进行学习，从而针对不同的系统状态做出优化的反应。强化学习具有良好的可扩展性，经过大量样本的离线训练，可以习得针对一类调度问题的优秀策略，实现动态调度条件下求解时间和求解质量的均衡。根据目前强化学习在调度领域应用的总结，可以得出如下研究结论：

1. 深度强化学习在调度领域崭露头角
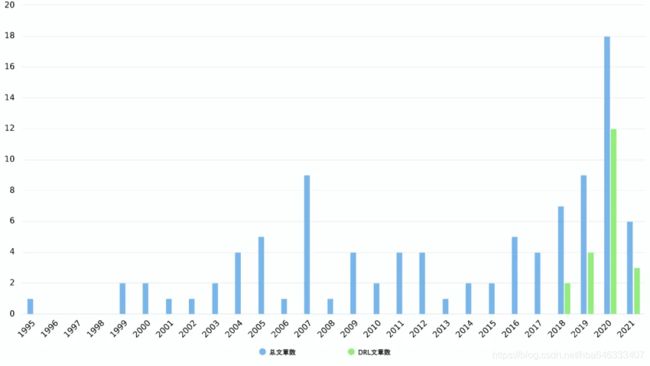
   从整体上看，研究强化学习求解生产调度问题的文章总数大概为97篇（见表3），图3为从1995年最早使用强化学习求解调度问题开始至今每年发表文章的数量分布，在2007年出现了一次小高潮，此时的研究者普遍采用人工神经网络来拟合大规模调度问题的值函数，但该方法会导致训练过程极其不稳定，直到2018年才开始有学者将深度强化学习应用到调度领域，并在随后的两三年里得到了广泛的应用。

图3 强化学习求解调度问题文章数量分布

2. 调度状态需要人工设计
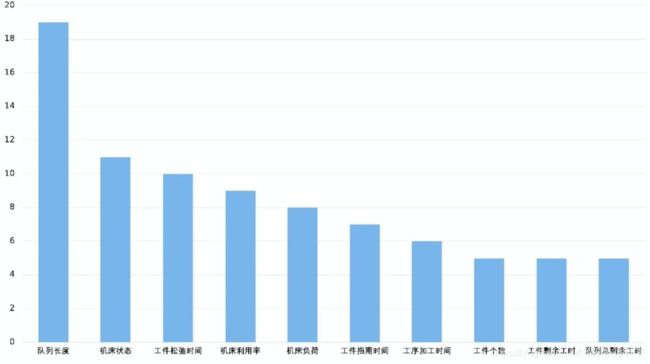
   这些文献中以手工设计调度状态为主，且队列长度、机床状态等为最常使用的调度属性，如图4所示。深度强化学习可以从原始输入中感知信息，借助该优势可设计一种将调度问题转化为图像的新型状态表达方式，由代理自行挖掘属性之间的关系而无需人工设计。
   

图4 强化学习常用的调度属性

3. 调度动作以选择启发式规则为主
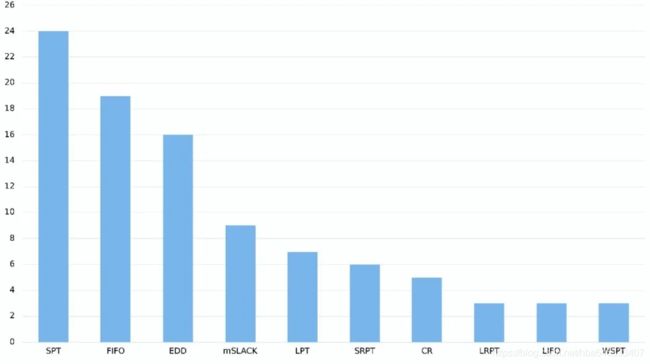
   大多数研究仍以根据不同调度状态选择启发式规则为主，且最短加工时间SPT、先入先出FIFO等为最常使用的调度规则，如图5所示。但是有限的规则集合不能完全覆盖所有排序结果，因此算法仅在规则空间中而不是解空间中进行搜索，可考虑直接输出工序排序而不是规则序列。

图5 强化学习常用的调度规则

4. 奖励函数设计视问题而定
   奖励函数与调度问题和调度目标息息相关，同时还会影响算法的收敛性能，因此目前奖励函数的设计需要“因地制宜”，主要有启发式奖励和等价奖励两种设计方法。启发式奖励可以和最终目标不等价，但在设计时需要一定的先验知识，而等价奖励则需要给出方法证明累积奖励和最终优化的目标是等价的。

5. 强化学习求解调度时考虑约束较少
   目前强化学习主要应用于求解作业车间调度问题，而对在实际车间中普遍存在的柔性作业车间调度问题研究较少，更别提具有分合批等实际约束的调度问题了，因此需要针对多约束的车间调度问题建立一个统一的调度求解框架。

表3 强化学习在调度中的应用

参考文献

[1] Zhang W, Dietterich T G. A Reinforcement Learning Approach to Job-Shop Schedulling[C]. Proc. of 14th Int. Joint Conf. on Artificial Intelligence, 1995: 1114-1120.
[2] Sutton R S, Barto A G. Reinforcement Learning: An Introduction[M]. Cambridge, Massachusetts: The MIT Press, 2018: 548.
[3] Williem R S, Setiawan K. Reinforcement learning combined with radial basis function neural network to solve Job-Shop scheduling problem[C]. 2011 IEEE International Summer Conference of Asia Pacific Business Innovation and Technology Management, 2011: 29-32.
[4] Paternina-Arboleda C D, Das T K. A multi-agent reinforcement learning approach to obtaining dynamic control policies for stochastic lot scheduling problem[J]. Simulation Modelling Practice and Theory, 2005, 13(5): 389-406.
[5] Rummukainen H, Nurminen J K. Practical Reinforcement Learning - Experiences in Lot Scheduling Application[J]. Ifac Papersonline, 2019, 52(13): 1415-1420.
[6] Wang J, Li X, Zhu X. Intelligent dynamic control of stochastic economic lot scheduling by agent-based reinforcement learning[J]. International Journal of Production Research, 2012, 50(16): 4381-4395.
[7] Fonseca-Reyna, Yunior, César, et al. Adapting a Reinforcement Learning Approach for the Flow Shop Environment with sequence-dependent setup time[J]. Revista Cubana de Ciencias Informáticas, 2017.
[8] Stefan P. Flow-shop scheduling based on reinforcement learning algorithm[J]. Production Systems and Information Engineering, 2003, 1(1): 83-90.
[9] Palombarini J A, Martinez E C. Automatic Generation of Rescheduling Knowledge in Socio-technical Manufacturing Systems using Deep Reinforcement Learning[M]. New York: Ieee, 2018.
[10] Palombarini J A, Martinez E C. Closed-loop Rescheduling using Deep Reinforcement Learning[J]. Ifac Papersonline, 2019, 52(1): 231-236.
[11] Liu C, Chang C, Tseng C. Actor-Critic Deep Reinforcement Learning for Solving Job Shop Scheduling Problems[J]. Ieee Access, 2020, 8: 71752-71762.
[12] Hu L, Liu Z Y, Hu W F, et al. Petri-net-based dynamic scheduling of flexible manufacturing system via deep reinforcement learning with graph convolutional network[J]. Journal of Manufacturing Systems, 2020, 55: 1-14.
[13] Seito T, Munakata S. Production Scheduling based on Deep Reinforcement Learning using Graph Convolutional Neural Network[M]. 2020.
[14] Lin C C, Deng D J, Chih Y L, et al. Smart Manufacturing Scheduling With Edge Computing Using Multiclass Deep Q Network[J]. Ieee Transactions on Industrial Informatics, 2019, 15(7): 4276-4284.
[15] Miyashita K. Learning scheduling control knowledge through reinforcements[J]. International Transactions in Operational Research, 2000, 7(2): 125-138.
[16] Wang Y C, Usher J M. Application of reinforcement learning for agent-based production scheduling[J]. Engineering Applications of Artificial Intelligence, 2005, 18(1): 73-82.
[17] Shahrabi J, Adibi M A, Mahootchi M. A reinforcement learning approach to parameter estimation in dynamic job shop scheduling[J]. Computers & Industrial Engineering, 2017, 110: 75-82.
[18] Shiue Y R, Lee K C, Su C T. Real-time scheduling for a smart factory using a reinforcement learning approach[J]. Computers & Industrial Engineering, 2018, 125: 604-614.
[19] Hu H, Jia X, He Q, et al. Deep reinforcement learning based AGVs real-time scheduling with mixed rule for flexible shop floor in industry 4.0[J]. Computers & Industrial Engineering, 2020, 149: 106749.
[20] Zhang Z C, Zheng L, Weng M X. Dynamic parallel machine scheduling with mean weighted tardiness objective by Q-Learning[J]. International Journal of Advanced Manufacturing Technology, 2007, 34(9-10): 968-980.
[21] Riedmiller S C, Riedmiller M A. A Neural Reinforcement Learning Approach to Learn Local Dispatching Policies in Production Scheduling[C]. Proceedings of the Sixteenth International Joint Conference on Artificial Intelligence, 1999: 764–771.
[22] Yang S, Xu Z, Wang J. Intelligent Decision-Making of Scheduling for Dynamic Permutation Flowshop via Deep Reinforcement Learning[J]. Sensors (Basel), 2021, 21(3).
[23] Yang H B, Yan H S. An adaptive approach to dynamic scheduling in knowledgeable manufacturing cell[J]. International Journal of Advanced Manufacturing Technology, 2009, 42(3-4): 312-320.
[24] 王国磊, 钟诗胜, 林琳. 基于聚类状态隶属度的动态调度Q-学习. 高技术通讯, 2009: 428-433.
[25] Wang H-X, Yan H-S. An interoperable adaptive scheduling strategy for knowledgeable manufacturing based on SMGWQ-learning[J]. Journal of Intelligent Manufacturing, 2016, 27(5): 1085-1095.
[26] Wang Y F. Adaptive job shop scheduling strategy based on weighted Q-learning algorithm[J]. Journal of Intelligent Manufacturing, 2018, 31(2): 417-432.
[27] Zhang Z C, Zheng L, Li N, et al. Minimizing mean weighted tardiness in unrelated parallel machine scheduling with reinforcement learning[J]. Computers & Operations Research, 2012, 39(7): 1315-1324.
[28] 王超, 郭静, 包振强. 改进的Q学习算法在作业车间调度中的应用. 计算机应用, 2008: 3268-3270.
[29] Kuhnle A, Röhrig N, Lanza G. Autonomous order dispatching in the semiconductor industry using reinforcement learning[J]. Procedia CIRP, 2019, 79: 391-396.
[30] Qu S H, Wang J, Shivani G: Learning Adaptive Dispatching Rules for a Manufacturing Process System by Using Reinforcement Learning Approach, 2016 Ieee 21st International Conference on Emerging Technologies and Factory Automation, New York: Ieee, 2016.
[31] Park J, Chun J, Kim S H, et al. Learning to schedule job-shop problems: representation and policy learning using graph neural network and reinforcement learning[J]. International Journal of Production Research, 2021: 1-18.
[32] Waschneck B, Reichstaller A, Belzner L, et al. Optimization of global production scheduling with deep reinforcement learning[J]. Procedia CIRP, 2018, 72: 1264-1269.
[33] Luo S. Dynamic scheduling for flexible job shop with new job insertions by deep reinforcement learning[J]. Applied Soft Computing, 2020, 91: 17.
[34] Aydin M E, Öztemel E. Dynamic job-shop scheduling using reinforcement learning agents[J]. Robotics and Autonomous Systems, 2000, 33(2): 169-178.
[35] Kong L F, Wu J. Dynamic single machine scheduling using Q-learning agent[C]. Machine Learning and Cybernetics, 2005. Proceedings of 2005 International Conference on, 2005.
[36] 杨宏兵, 严洪森. 知识化制造系统中动态调度的自适应策略研究. 控制与决策, 2007: 1335-1340,1346.
[37] Hong J, Prabhu V V. Distributed Reinforcement Learning Control for Batch Sequencing and Sizing in Just-In-Time Manufacturing Systems[J]. Applied Intelligence, 2004, 20(1): 71-87.
[38] Stricker N, Kuhnle A, Sturm R, et al. Reinforcement learning for adaptive order dispatching in the semiconductor industry[J]. CIRP Annals, 2018, 67(1): 511-514.
[39] Wang Y C. Application of reinforcement learning to multi-agent production scheduling[D]. Mississippi State University, M1 - Degree of Doctor of Philosophy, 2003: Pages.
[40] Wang Y C, Usher J M. Learning policies for single machine job dispatching[J]. Robotics and Computer-Integrated Manufacturing, 2004, 20(6): 553-562.
[41] 汪浩祥, 严洪森, 汪峥. 知识化制造环境中基于双层Q学习的航空发动机自适应装配调度. 计算机集成制造系统, 2014: 3000-3010.
[42] Gabel T, Riedmiller M. Adaptive Reactive Job-Shop Scheduling with Reinforcement Learning Agents[J]. International Journal of Information Technology and Intelligent Computing, 2007.
[43] Gabel T, Riedmiller M. Scaling Adaptive Agent-Based Reactive Job-Shop Scheduling to Large-Scale Problems[C]. 2007 IEEE Symposium on Computational Intelligence in Scheduling, 2007: 259-266.
[44] Wei Y Z, Zhao M Y. Composite rules selection using reinforcement learning for dynamic job-shop scheduling[M]. New York: Ieee, 2004.
[45] Aissani N, Bekrar A, Trentesaux D, et al. Dynamic scheduling for multi-site companies: a decisional approach based on reinforcement multi-agent learning[J]. Journal of Intelligent Manufacturing, 2012, 23(6): 2513-2529.
[46] Martínez Y, Nowé A, Suárez J, et al. A Reinforcement Learning Approach for the Flexible Job Shop Scheduling Problem[C]. Learning and Intelligent Optimization, 2011: 253-262.
[47] Bouazza W, Sallez Y, Aissani N, et al.: A Model for Manufacturing Scheduling Optimization Through Learning Intelligent Products, Borangiu T, Thomas A, Trentesaux D, editor, Service Orientation in Holonic and Multi-agent Manufacturing, Cham: Springer International Publishing, 2015: 233-241.
[48] Park I B, Huh J, Kim J, et al. A Reinforcement Learning Approach to Robust Scheduling of Semiconductor Manufacturing Facilities[J]. Ieee Transactions on Automation Science and Engineering, 2020, 17(3): 1420-1431.
[49] Shi D, Fan W, Xiao Y, et al. Intelligent scheduling of discrete automated production line via deep reinforcement learning[J]. International Journal of Production Research, 2020, 58(11): 3362-3380.
[50] Chen X, Hao X, Lin H W, et al. Rule driven multi objective dynamic scheduling by data envelopment analysis and reinforcement learning[C]. 2010 IEEE International Conference on Automation and Logistics, 2010: 396-401.
[51] Qu S H, Chu T S, Wang J, et al.: A Centralized Reinforcement Learning Approach for Proactive Scheduling in Manufacturing, Proceedings of 2015 Ieee 20th Conference on Emerging Technologies & Factory Automation, New York: Ieee, 2015.
[52] Qu S, Wang J, Govil S, et al. Optimized Adaptive Scheduling of a Manufacturing Process System with Multi-skill Workforce and Multiple Machine Types: An Ontology-based, Multi-agent Reinforcement Learning Approach[J]. Procedia CIRP, 2016, 57: 55-60.
[53] 肖鹏飞, 张超勇, 孟磊磊, et al. 基于深度强化学习的非置换流水车间调度问题. 计算机集成制造系统, 2019: 1-19.
[54] 孙晟, 王世进, 奚立峰. 基于强化学习的模式驱动调度系统研究. 计算机集成制造系统, 2007: 1795-1800.
[55] 王世进, 孙晟, 周炳海, et al. 基于Q-学习的动态单机调度. 上海交通大学学报, 2007: 1227-1232+1243.
[56] Tanaka Y, Yoshida T. An application of reinforcement learning to manufacturing scheduling problems[C]. IEEE SMC’99 Conference Proceedings. 1999 IEEE International Conference on Systems, Man, and Cybernetics (Cat. No.99CH37028), 1999: 534-539 vol.4.
[57] 潘燕春, 冯允成, 周泓, et al. 强化学习和仿真相结合的车间作业排序系统. 控制与决策, 2007: 675-679.
[58] Zhang Z, Wang W, Zhong S, et al. Flow shop scheduling with reinforcement learning[J]. Asia-Pacific Journal of Operational Research, 2013, 30(05): 1350014.
[59] Liu C C, Jin H Y, Tian Y, et al. Reinforcement learning approach to re-entrant manufacturing system scheduling[C]. 2001 International Conferences on Info-Tech and Info-Net. Proceedings (Cat. No.01EX479), 2001: 280-285 vol.3.
[60] Ou X, Chang Q, Arinez J, et al. Gantry Work Cell Scheduling through Reinforcement Learning with Knowledge-guided Reward Setting[J]. Ieee Access, 2018, 6: 14699-14709.
[61] Zhou T, Tang D B, Zhu H H, et al. Reinforcement Learning With Composite Rewards for Production Scheduling in a Smart Factory[J]. Ieee Access, 2021, 9: 752-766.
[62] 杨能俊, 郭宇, 方伟光, et al. 实时数据驱动的离散制造车间自适应调度方法. 组合机床与自动化加工技术, 2020: 175-179+184.
[63] Arviv K, Stern H, Edan Y. Collaborative reinforcement learning for a two-robot job transfer flow-shop scheduling problem[J]. International Journal of Production Research, 2016, 54(4): 1196-1209.
[64] 杨宏兵, 沈露, 成明, et al. 带退化效应多态生产系统调度与维护集成优化. 计算机集成制造系统, 2018: 80-88.
[65] Stern H, Arviv K, Edan Y. Flow-Shop Robotic Scheduling Problem with Collaborative Reinforcement Learning[C]. International Conference on Production Research, 2011.
[66] Palombarini J, Martínez E. SmartGantt – An intelligent system for real time rescheduling based on relational reinforcement learning[J]. Expert Systems with Applications, 2012, 39(11): 10251-10268.
[67] Lee J-H, Kim H-J. Reinforcement learning for robotic flow shop scheduling with processing time variations[J]. International Journal of Production Research, 2021: 1-23.
[68] Méndez-Hernández B M, Rodríguez-Bazan E D, Martinez-Jimenez Y, et al. A Multi-objective Reinforcement Learning Algorithm for JSSP[C]. Artificial Neural Networks and Machine Learning – ICANN 2019: Theoretical Neural Computation, 2019: 567-584.
[69] 张东阳, 叶春明. 应用强化学习算法求解置换流水车间调度问题. 计算机系统应用, 2019: 195-199.
[70] Ren J F, Ye C M, Yang F. A NOVEL SOLUTION TO JSPS BASED ON LONG SHORT-TERM MEMORY AND POLICY GRADIENT ALGORITHM[J]. International Journal of Simulation Modelling, 2020, 19(1): 157-168.
[71] Li Z P, Wei X M, Jiang X S, et al. A Kind of Reinforcement Learning to Improve Genetic Algorithm for Multiagent Task Scheduling[J]. Mathematical Problems in Engineering, 2021, 2021: 12.
[72] 陈勇, 王昊天, 易文超, et al. 基于元胞机与强化学习的多扰动车间调度算法. 计算机集成制造系统, 2020: 1-24.
[73] Zhao F, Zhang L, Cao J, et al. A cooperative water wave optimization algorithm with reinforcement learning for the distributed assembly no-idle flowshop scheduling problem[J]. Computers & Industrial Engineering, 2021, 153: 107082.
[74] Rabelo L, Jones A, Yih Y. Development of a real-time learning scheduler using reinforcement learning concepts[C]. Proceedings of the 1994 IEEE International Symposium on Intelligent Control, 1994: 291-296.
[75] Bouazza W, Sallez Y, Beldjilali B. A distributed approach solving partially flexible job-shop scheduling problem with a Q-learning effect[J]. IFAC-PapersOnLine, 2017, 50(1): 15890-15895.
[76] Han B A, Yang J J. Research on Adaptive Job Shop Scheduling Problems Based on Dueling Double DQN[J]. Ieee Access, 2020, 8: 186474-186495.
[77] Wei Y, Jiang X, Hao P, et al. Multi-agent Co-evolutionary Scheduling Approach Based on Genetic Reinforcement Learning[C]. 2009 Fifth International Conference on Natural Computation, 2009: 573-577.
[78] Li S, Ma Y, Lu X, et al. Adaptive Scheduling for Smart Shop Floor Based on Deep Q-Network[C]. 2020 IEEE 16th International Conference on Automation Science and Engineering (CASE), 2020: 618-623.
[79] 张智聪, 郑力, 翁小华. 基于增强学习的平行机调度研究. 计算机集成制造系统, 2007: 110-116.
[80] Pinedo M, Reed J. The “least flexible job first” rule in scheduling and in queueing[J]. Operations Research Letters, 2013, 41(6): 618-621.
[81] Bianchi R a C, Ribeiro C H C, Costa A H R. Heuristically Accelerated Q–Learning: A New Approach to Speed Up Reinforcement Learning[C]. Advances in Artificial Intelligence – SBIA 2004, 2004: 245-254.
[82] Csaji B C, Monostori L: Stochastic reactive production scheduling by multi-agent based asynchronous approximate dynamic programming, Pechoucek M, Petta P, Varga L Z, editor, Multi-Agent Systems and Applications Iv, Proceedings, Berlin: Springer-Verlag Berlin, 2005: 388-397.
[83] Fonseca-Reyna Y, Martinez Y, Rodríguez-Sánchez E, et al. AN IMPROVEMENT OF REINFORCEMENT LEARNING APPROACH TO PERMUTATIONAL FLOW SHOP SCHEDULING PROBLEM[C]. 13th INTERNATIONAL CONFERENCE on OPERATIONS RESEARCH (ICOR 2018), 2019.
[84] Fonseca-Reyna Y C, Martínez-Jiménez Y, Cabrera A V, et al. Optimization of heavily constrained hybrid-flexible flowshop problems using a multi-agent reinforcement learning approach[J]. Investigación Operacional, 2019, 40(1): 100-111.
[85] 王凌, 潘子肖. 基于深度强化学习与迭代贪婪的流水车间调度优化. 控制与决策, 2020: 1-9.
[86] Pan R, Dong X, Han S. Solving Permutation Flowshop Problem with Deep Reinforcement Learning[C]. 2020 Prognostics and Health Management Conference (PHM-Besanon), 2020: 349-353.
[87] Csáji B C, Monostori L, Kádár B. Reinforcement learning in a distributed market-based production control system[J]. Advanced Engineering Informatics, 2006, 20(3): 279-288.
[88] Gabel T. Multi-Agent Reinforcement Learning Approaches for Distributed Job-Shop Scheduling Problems[D]. Universität Osnabrück, 2009: Pages.
[89] Chen M. Policy based reinforcement learning approach Of Jobshop scheduling with high level deadlock detection[D]. Ames, Iowa: Iowa State University, 2014: Pages.
[90] 何彦, 王乐祥, 李育锋, et al. 一种面向机械车间柔性工艺路线的加工任务节能调度方法. 机械工程学报, 2016: 168-179.
[91] 王维祺, 叶春明, 谭晓军. 基于Q学习算法的作业车间动态调度. 计算机系统应用, 2020: 218-226.
[92] Zhang C, Song W, Cao Z, et al. Learning to Dispatch for Job Shop Scheduling via Deep Reinforcement Learning[J]. Advances in neural information processing systems, 2020, 33.
[93] Chen R H, Yang B, Li S, et al. A self-learning genetic algorithm based on reinforcement learning for flexible job-shop scheduling problem[J]. Computers & Industrial Engineering, 2020, 149: 12.
[94] 王利存, 郑应平. 开环可重入排队网络的递阶增强型学习调度. 系统工程理论与实践, 2002: 76-80+102.
[95] 柳长春, 沈志江, 于海斌. 可重入生产系统的平均报酬型强化学习调度. 信息与控制, 2004: 145-150.
[96] Jin Young C, Reveliotis S. Relative value function approximation for the capacitated re-entrant line scheduling problem[J]. Ieee Transactions on Automation Science and Engineering, 2005, 2(3): 285-299.
[97] Zhang Z. Reinforcement learning based scheduling in semiconductor final testing[C]. 2010 IEEE International Conference on Industrial Engineering and Engineering Management, 2010: 1693-1697.
[98] Zhang Z, Zheng L, Hou F, et al. Semiconductor final test scheduling with Sarsa(λ,k) algorithm[J]. European Journal of Operational Research, 2011, 215(2): 446-458.
[99] Wang H, Sarker B R, Li J, et al. Adaptive scheduling for assembly job shop with uncertain assembly times based on dual Q-learning[J]. International Journal of Production Research, 2020: 1-17.
[100] Drakaki M, Tzionas P. Manufacturing Scheduling Using Colored Petri Nets and Reinforcement Learning[J]. Applied Sciences, 2017, 7(2): 136.