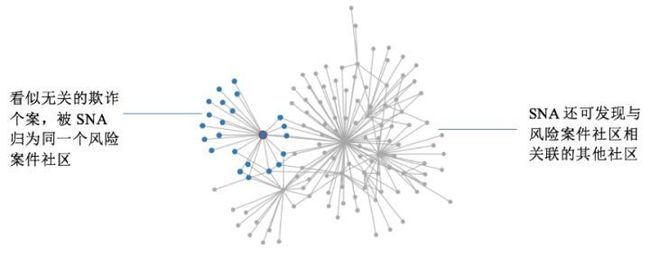
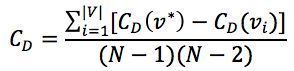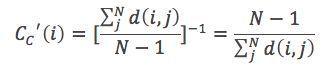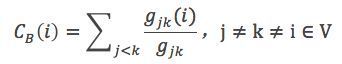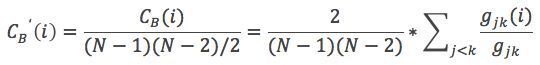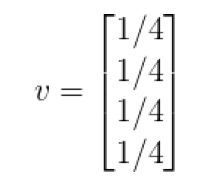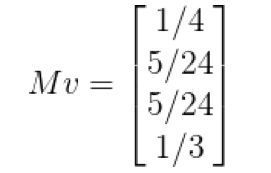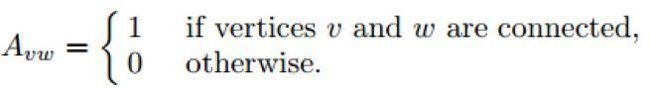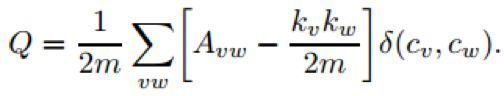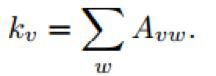基于社交网络分析算法（SNA）的反欺诈（二）

基于社交网络分析算法（SNA）的反欺诈（一） 

社交网络分析算法并不新鲜，且已经广泛应用于社交人物影响力计算、好友和商品推荐、社交圈子分析等领域。近几年，社交网络分析算法的应用不断拓展，已经开始应用于各种金融和保险等反欺诈领域，且效果很好。

为了讲解基于SNA的反欺诈，我先简单介绍下SNA的原理。为了方便理解，我会直接忽略很多细节（例如：入度和出度的概念），以下内容都是为了有助于理解反欺诈建模，想了解SNA更系统的知识请参看其他材料。

#基础知识#

节点（Vertice）和边（Edge）

社交网络，顾名思义，就是表现人和人之间关系的网络。类似的，社交网络分析算法，也就是为了研究节点（可以理解成人）和节点关系（边，可以理解成人和人之间的关系）的算法。通过对关系的研究，可以对节点关系做梳理，从而聚成团。

为了方便对下文指标的理解，我们定义节点数 N = |V|, 边数 M = |E|

图（Graph），有向图，无向图

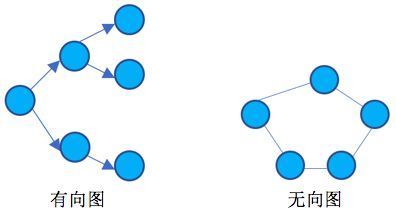
用边把节点连接起来形成的网络，称为图（Graph）。图又可以分成无向图和有向图，如下图所示：

无向图仅表示节点和节点之间是否有关系，例如：在P2P行业反欺诈建模中，我们通过申请者通讯录去获取其社会关系，例如，如果张三和李四的通讯录都有老赖王五，那么，张三和李四的贷款申请违约风险就会比较高。

有向图相比于无向图会携带方向信息，一个最简单的例子就是传销图。传销有非常成熟的上下线制度，是发展团队十分迅速有效的手法，也被互联网公司广泛用于发展用户——好友邀请制度，此外，保险销售公司也有类似的提成机制。如被不法分子利用规则，对互联网公司，产生的后果就是大规模虚假注册；对保险销售公司，产生的后果就是内外勾结骗取额外提成。

社区（Community），非重叠社区，重叠社区

社区可以理解成UML中的群组，也就是同一个社区中节点和节点关系紧密，而社区和社区之间关系稀疏。

如果任意两个社区的节点集合的交集为空则被称为非重叠社区，否则称为重叠社区。

派系（Clique），完全子图

派系是指任意两个点都相连的节点的集合，又称为完全子图。

#分析指标#

指标一：度

简单来讲，度就是指从你这个节点发散出去了多少条边，或者可以理解成你有多少个朋友。

指标二：度中心性

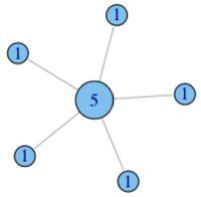
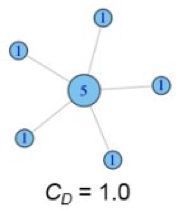
我们在每个节点上都标注上其度的值大小，如下图所示：

我们接下来做标准化处理，用度除以最大连接可能（N-1），则得到：

形象地讲，中心性指越高，表示与你有联系的人越多，或者说，你的社交人物影响力就大。这是一个社交网站分析用户行为时一个常用的指标。

指标三：集中度（Centrality）

集中度表示一个群体的紧密程度，或者可以理解成密度。集中度又可以分为度集中度，紧密集中度和介数集中度，还有图集中度、特征向量集中度等，以下我们主要介绍前三种。

3.1 度集中度（Degree centrality）

度量集中度的方式有很多，例如，基尼系数、标准差和Freeman集中度公式。以下，我们以Freeman集中度通用公式为例计算：

其中，v*指度最大的节点。

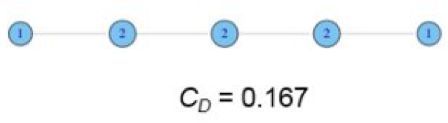
根据上述公式计算如下两图的度集中度：

3.2 紧密集中度（Closeness centrality）

依赖于从一个结点出发到其它所有结点的最短路径长度，并被定义为总长度的倒数。

节点i的紧密中心如下所示：

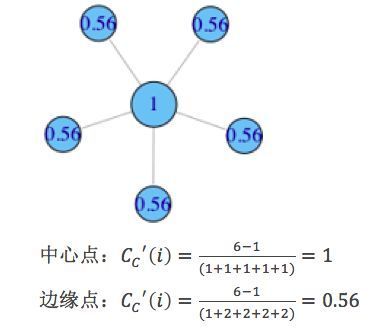
而通常我们讲紧密中心度，是指其标准化形式，也即总距离长除以(N-1)

3.3 介数集中度（betweenness centrality）

直观理解，介数就是多少个节点对必须经过本节点实现最小跳数互达。定义如下：

其中，gjk表示节点jk最短路径的个数，gjk(i)表示i位于最短路径的个数。

同样，我们将其标准化，除以除本节点外其他节点对个数，得到：

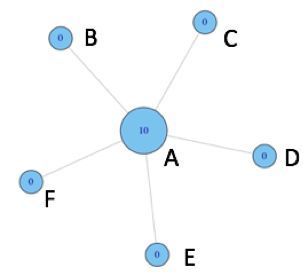
还是以下面两图作为示例来计算介数集中度：

A在(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)十个节点对的最短路径上，非标准化值为10；

BCDEF不在任何节点对的最短路径上，所以非标准化值为0。

简单解释一下：

对于节点A和E，都不在任何节点对的最短路径上，所以为0；

对于节点B，在（A,C）,(A,D)和(A,E)三个节点对最短路径上，非标准化值为3。类似地，节点D与B情况相同，也为3；

对于节点C，在（A,D）,(A,E),(B,D)和（B,E）四个节点对最短路径上，非标准化值为4。

感谢作者mryqu：http://blog.sina.com.cn/s/blog_72ef7bea0102v748.html

感谢作者du00cs: http://blog.sina.com.cn/s/blog_439371b501012lgt.html

感谢作者fionaplanet：http://www.cnblogs.com/fionacai/p/6262527.html

 

基于社交网络分析算法（SNA）的反欺诈（二）

关于SNA基础知识和指标，可参看本系列文章《基于社交网络分析算法（SNA）的反欺诈（一）》，本文主要讲SNA算法。

算法一：PageRank算法

PageRank算法用一句古文来讲，就是“近朱者赤，近墨者黑”，也就是被高质量网页引用的网页也是高质量网页，或者被用户访问越多的网页可能质量越高。我们在大学写论文投期刊的时候，也会看到类似的数字，比如：期刊的影响因子、被引用次数。影响因子和被引用次数越高，表示这个期刊越好，如果被这样的期刊录用，也表示你的学术水平得到了极大的认可。再比如，相信每个支付宝用户都受到过芝麻信用的善意提醒：多结交信用度高的朋友，有助于提高自己的芝麻分，也是一样的道理。《黑镜》第三季第一集便是把信用评分社会夸张到极致，也是对社交网络的一种诠释。

PageRank算法被广泛用于搜索引擎结果排序，而为了抵御Spam，各搜索引擎采用的排名算法实际上是保密的，PageRank的具体计算方法也不尽相同。这里，我只讲一种最简单，但也可以揭示PageRank本质的算法——基于页面链接属性的PageRank算法。

背景假设：

（1） 全世界只有4个网页，ABCD，我们讲每个网页抽象成一个节点；

（2） 如果页面A有链接指向B，我们就认为有一条从A到B的有向边；

（3） 假设一个用户停留在某一页面时，跳转到页面上每个链接的概率是相等的；

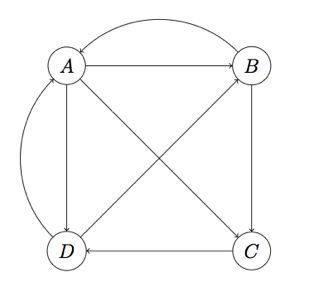
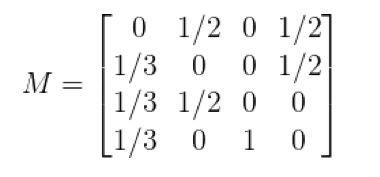
那么，假设我们根据以上背景，绘制了这4个网页的关系图，如下：

我们定义这个一个矩阵，其第i行j列第值表示用户从页面j跳转到i的概率，并将其命名为转移矩阵（transition Matrix）。那么，我们绘制上图的转移矩阵M，如下：

为了计算每个网页的rank值，我们先初始化各页面值，令其相等。在这个例子中，也就是ABCD都是1/4。那么，建立rank值的初始向量v：

那么，一个用户来到这个网页，随机点开网页，会使四个页面的rank值更改至如下：

第二个人来，再次点击，会再次更改rank为MMv，如此这般不断迭代，最终rank值会不断收敛到某个设定的阈值，得到的值就是整个页面的PageRank值。再这个例子中，大约收敛到（A，B，C，D）T=（1/4，1/4，1/5，1/4）T。

实际应用中，网页外链到其他网页的概率并不相同，或者可能停留在此页面，可以增加一个阻尼因子（a）表示用户停留当前页面不链接到其他页面的概率。

算法二：社区发现算法

社区发现算法的思路就是在复杂网络中发现连接紧密的节点簇（社区结构），与聚类的思路如出一辙。发现这些社区结构的方式有很多中，本文主要介绍几种简单但常用的算法：GN算法，Louvain算法，LPA算法和SLPA算法。

2.1 GN（Girvan-Newman）算法

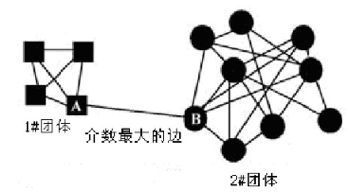
GN算法是一个最经典的社区发现算法，属于分裂的层次聚类算法（自上而下）。因最初由MichelleGirvan和Mark Newman提出而得名。GN算法的基本思想是不断删除网络中具有相对于所有源节点的最大边介数的边，然后，再重新计算网络中剩余的边的相对于所有源节点的边介数，重复这个过程，直到网络中所有的边都被删除。怎么理解呢？通过介数的定义我们知道，介数是多少个节点对必须经过本节点实现最小跳数互达的值，而介数高的边必然要比介数低的边更可能是社区之间的边（两个社区中的节点之间的最短路径都要经过那些社区之间的边，所以它们的介数会很高）。为了方便理解，可以参看下图，方块节点和圆形节点的最短路径，必然要经过边AB，因此边AB的介数最大，拆除这条边，就可以将其分成1#和2#两个团体了，或者称之为两个社区。

然而，虽然GN算法的准确率很高，但是计算量大，时间复杂度也很高。

2.2 Louvain算法

Louvain可以理解成GN的逆过程，GN的思路是不断拆边，类似于自上而下的层次聚类。而Louvain则是不断凝聚，类似于自下而上的层次聚类。为了理解Louvain算法的过程，我们先来学习一个社区评价指标——模块度。

模块度（Modularity）用来衡量一个社区的划分是不是相对比较好的结果。一个相对好的结果在社区内部的节点相似度较高，而在社区外部节点的相似度较低。

设Avw为网络的邻接矩阵的一个元素，定义为：

假设cv和cw分别表示点v和点w所在的两个社区，社区内部的边数和网络中总边数的比例：

函数δ(cv,cw)的取值定义为：如果v和w在一个社区，即cv=cw，则为 1，否则为 0。m为网络中边的总数。

模块度的大小定义为社区内部的总边数和网络中总边数的比例减去一个期望值，该期望值是将网络设定为随机网络时同样的社区分配所形成的社区内部的总边数和网络中总边数的比例的大小，于是模块度Q为：

其中kv表示点v的度。

在进行每次划分的时候计算Q值，Q取值最大的时候则是此网路较理想的划分。Q值的范围在0-1之间，Q值越大说明网络划分的社区结构准确度越高，在实际的网络分析中，Q值的最高点一般出现在0.3-0.7之间。

好，介绍完模块度，我们就可以开始使用Louvain算法了。首先，我们把每一个节点当作一个独立的社区，假如我们把V1和V2加入到i都会使其模块度增加， 我们比较两者的数值，选择增量较大的一个加入到i社区中。如此这般反复迭代，直到模块度Q的值不再增加为止。

3.3 LPA（Label Propagation Algorithm）

LPA算法的稳定性不是很好，但优点是可扩展性强，时间复杂度接近线性，且可以控制迭代次数来划分节点类别，不需要预先给定社区数量，适合处理大规模复杂网络。LPA的计算步骤也十分简单：

第一步：为所有节点指定一个唯一标签；

第二步：刷新标签：对于某一个节点，考察其所有邻居节点的标签，并进行统计，将出现个数最多的那个标签赋给当前节点（如果最多的标签不唯一，随机选择一个）；

第三步：重复步骤二，直到收敛为止。

3.4 SLPA （Speaker-listener Label Propagation Algorithm）

SLPA是一种改进的LPA，是一种重叠社区发现算法，其中涉及一个重要的阈值参数r。通过对r的适当选取，可将其退化为非重叠型。

SLPA算法思路

SLPA中引入了listener和speaker两个比较形象的概念。可以这么理解：在刷新节点的过程中，我们将要被刷新的节点定义为listener，其临近节点就是它的speaker，speaker通常不止一个，在众多speaker七嘴八舌时，listener该听谁的呢？这时我们就要制定一个规则。

在LPA中，我们以出险次数最多的标签来做决断，这其实就是一种规则。只不过在SLPA框架里，规则的选取方式多由用户指定（通常结合业务逻辑和场景决定）。

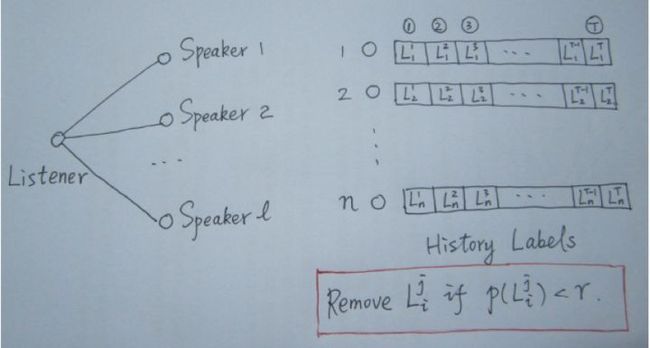
与LPA相比，SLPA最大的特点在于它不是仅仅的刷新替代原标签，而是记录每一个节点在刷新迭代过程中的历史标签序列（例如迭代T此，则每一个节点将保留一个长度为T的序列，见上面著名的手绘图）。当迭代停止时，对每一个节点历史标签序列中各标签出现的频率做统计，按照某一个给定的阈值过滤掉那些出现概率小的标签，剩下的标签为该节点的标签（通常有多个）。

PS: SLPA后来被作者改名为GANXiS

感谢作者张洋：http://blog.jobbole.com/23286/

感谢作者八刀一闪：https://www.jianshu.com/p/44c4206979a6

感谢作者皮果提：http://blog.csdn.net/cleverlzc/article/details/39494957

 

基于社交网络分析算法（SNA）的反欺诈（三） 

关于社交网络分析算法的基础知识、评价指标和常用算法思路请参看本系列的前两篇文章《基于社交网络分析算法（SNA）的反欺诈（一）》和《基于社交网络分析算法（SNA）的反欺诈（二）》，本文主要讲社交网络算法的应用。

应用一：消费金融反欺诈

近年来，消费金融行业快速发展，相比于传统商业银行，形成了自己独特的优势：填写字段少、在线操作、审核速度快、放贷及时。这类申请人群通常因缺乏征信信息（一是客户年轻化，二是一些消费金融公司不具有查询征信的资格）而给消费金融企业带来了巨大的信用和欺诈风险。

如何在有限信用记录甚至是“零”信用记录下进行更准确的风险控制和欺诈识别是消费金融公司降本增效的关键问题。

解决这个问题通常有两种方案，一是运用商业银行广泛使用的成熟的评分卡模型；二是新兴的基于机器学习的信用预测（评分）模型。事实上，巧妙利用机器学习，可以将两种方案结合，互为补充。

机器学习的原料是数据，数据主要分为三类：一是用户主动提交的申请表信息；二是企业主动获取的信息，如：用户行为数据，设备数据，通讯录等；三是第三方数据（征信公司、运营商、社保公积金中心、法院执行、医院等）。

有了数据，第二步就是要进行特征工程，这也是整个算法中最核心的一步。对此，作者的文章《反欺诈建模之数据预处理（文末有福利）》有比较详细的介绍，在此不再赘述。

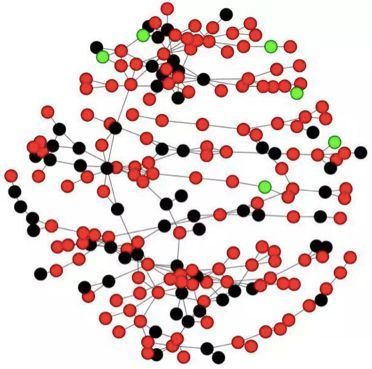
第三步，跑模型。由于本系列我们的主角是SNA，我们看下面一个典型社区。

图中，红色的点代表被拒绝的用户，黑色的点代表穿越用户（通过申请但有预期表现的用户），绿色的点代表通过且表现良好的用户。总结一下，该团伙的拒绝率达到66.8%，说明该团伙的平均用户信用值较低；穿越用户占所有通过用户的91.4%，进一步验证了该团伙的欺诈性。

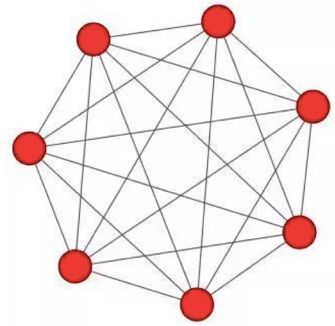
特别地，在利用SNA进行社区分析时，派系图具有更高的风险性。这种图的背后通常是多人协作的团伙作案，其两两互通表示两两认识，背后的目的多为相互勾结，伪造信息以达到消费金融借贷审核要求，且这类社群多有内外勾结的情况，需要重点关注。

应用二：信用卡申请反欺诈

信用卡申请欺诈与消费金融类似，只是目前，信用卡线上化平均水平只有70%，且有些银行甚至还没有开始采集设备信息，因此缺乏一些在线电子化信息。但由于信用卡中心具有查询用户征信数据的资质，所以相比于消费金融，会增加征信数据，对模型输入是一个很好的补充。

应用三：保险理赔反欺诈

SNA应用于保险理赔反欺诈已经有几年的时间了，据某保险公司产险风控部专家透露，自其上线SNA算法后，每年可提高预检率2%，多识别出400+欺诈团伙，为公司节约2亿+虚假理赔款。

车险理赔欺诈案件的识别，通常是利用车辆涉案人员、包括司机、报案人、受益人和伤者，以及修理厂、报案电话、检修地点、GPS信息等数据进行SNA分析，识别可能的骗保团伙。例如，平安保险林晟副总经理在2015年分享的一个案例：有两个上海车牌车辆与两个江苏车牌车辆发生了碰撞事故，单看感觉每个案件都很正常，但把他们放到SNA网络时，发现这个车的司机时那个案件的伤者，而一个案件的报案人又是另一个案件的司机。通过进一步调查分析，发现两个驾驶员驾驶不同车辆，一年内共5次出险。

还有一个典型案例，可以与大家分享：

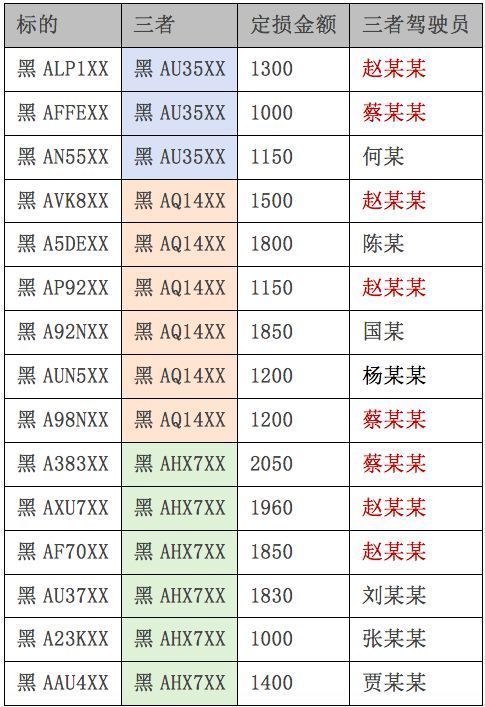
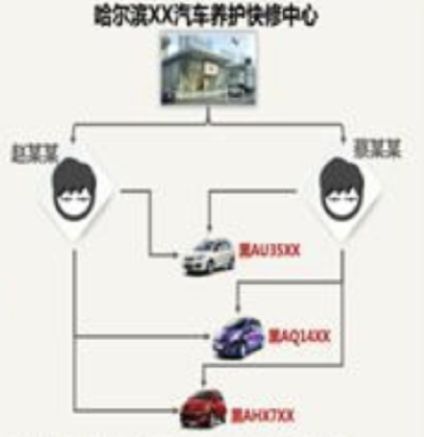
一修理厂员工通过驾驶道具车，充当三者，故意制造双方事故，短期内高频出险，利用交警“微损案件快速处理”的漏洞，自行拍摄车辆损失代替现场勘查，骗取保险赔款。通过SNA分析，除了修理厂的赵某某和蔡某某外，还发现了其他7名驾驶员，一举拿下这个骗保团伙。

由于现在各保险公司的价格都已经不断趋于同质化，而对于保险人选择保险公司的依据也早已不是单独的价格敏感了，快速理赔已经成为保险公司吸引保险人的重要因素之一了。因此有不法分子利用小额（<5000元）理赔便利，进行高频出险骗保，SNA网络可以有效识别这一类骗保行为，将骗保团伙一网打尽。

应用四：销售网络反欺诈

销售网络反欺诈是有向图的一个典型应用。为了促进销售量，很多公司在促销产品和服务时，都有发展二级代理或更下级代理的提成策略。而通常下级代理在卖出产品或服务时，上级代理会得到销售公司的额外奖励。例如，某保险销售公司，如果二级代理销售出一份保险，上级代理可获得销售公司额外的1%提成。如此，上级代理便利用这个规则，将自己的保单全部挂在二级代理上，以此获得不法收入。据统计，仅一年时间，某销售网点就利用销售提成奖励机制获取800万额外提成（涉案金额8000万元人民币）

特别感谢：本系列文章是基于维基百科、博客、微博等网络素材和黄姐姐实际项目经验所作，在此特别感谢所有提供素材的作者和客户爸爸们。