VIT模型个人笔记

前言

VIT模型即vision transformer，其想法是将在NLP领域的基于自注意力机制transformer模型用于图像任务中，相比于图像任务中的传统的基于卷积神经网络模型，VIT模型在大数据集上有着比卷积网络更强的效果和更节约的成本。

transformer

transformer模型是用于自然语言处理的一个基于注意力机制的模型，其图如下所示，该模型主要由解码器和编码器两部分组成。在nlp相关任务中，处理的数据对象主要是句子或句子对，因此，在训练之前，存在一个由多个token组成的字典。而输入模型的数据为形如大小为NF的向量，其中N为tokens的数量，F为表示每个token语义信息的向量长度，然后通过线性变化，加入位置信息得到大小为ND的向量，其中D为论文规定的输入给注意力层的向量大小。

注意力机制

从人认识句子的模式考虑，面对一个句子的多个单词时，我们对于不同的词组的关注度自然也存在不同，基于这个想法提出的注意力机制的抽象模型如下：query表示待处理目标，key-value表示键值对，输出attention本质上为values的加权和，而这里的权重即为注意力系数，其计算公式如下:其中，Q K分别表示query和健值的向量矩阵，dk为二者的大小。另外，还可将QK分为多个子矩阵的拼接，分别计算注意力，最后将结果拼接回去原来的大小。这种方法称为多头注意力机制

从transformer到VIT

若想将transformer模型用于对于二维图像的处理，首先需要解决的问题即是如和将二维图像转化为可输入给transformer模型的1维向量，自然想到将大小维NN的图像分为pp的小图像patch，再将每个patch展开这样得到大小维度为（NN/PP)(PP*3)的向量，3表示rgb三通道，再将该向量经过一个线性变化使其特征维度变为D，即可继续输入给transformer进行训练。其模型结构图如下：

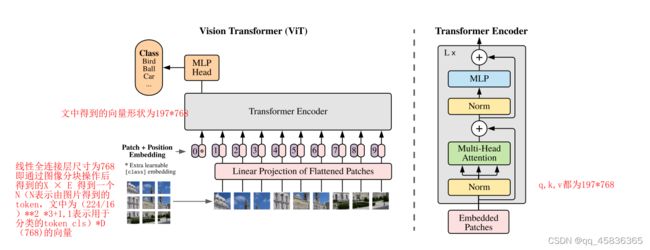
如图所示，在做图像分类任务时，需要增加一个表示类别的,token,最后在加上位置编码信息，得到的向量作为最终的transformer的输入。另外，在vit模型中，QKV都是同样来自图像patch的同样大小的三个向量。
整个流程用公式表示如下所示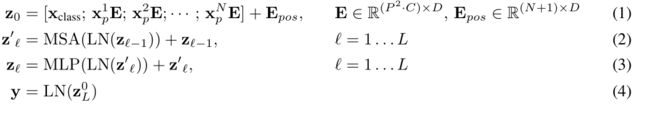其中第一步即图像的预处理，包扩图像分块，增加类别信息，位置信息，E表示将表示图像信息的向量通过线性变化进行维度转化；第二个式子为MSA部分，包括多头自注意力、跳跃连接 (Add) 和层规范化 (Norm) 三个部分，可以重复L个MSA block；第三个式子为MLP部分，包括前馈网络 (FFN)、跳跃连接 (Add) 和层规范化 (Norm) 三个部分。

代码实现

pytorch中可直接调用搭建vit模型，相关代码如下所示：

```python
import torch
import numpy as np
from vit_pytorch import ViT
import torchvision
from torchsummary import summary

#创建VIt模型实例
v=ViT(
    image_size=256,           #原始图像大小 256*256
    patch_size=32,            #图像块的大小，即将原始图像按块大小切割
    num_classes=10,           #分类数量
    dim=1024,                 #transformer隐藏变量维度。即输入给transform模型的特征维度
    depth=6,                  #transform编码器层数
    heads=6,                  #msa中多头注意力机制的头数
    mlp_dim=2048,                
    dropout=0.1,
    emb_dropout=0.1)

如输入一个图像，能得到一个分类结果。

```python
img=torch.randn(1,3,256,256)        #batch_size*C*h*w
preds=v(img)
preds.size()

##从头搭建vit模型
通过上面的模型原理介绍，VIT模型其实是以transformer为基础的，因此需要先搭建ffn，注意力机制等组件，再将其与图像预处理，编码嵌入层等拼接起来得到一个完整的vit模型

import torch
from torch import nn , einsum
import torch.nn.functional as F
from einops import rearrange , repeat     #einops是一个处理张量的第三方库 output_tensor = rearrange(input_tensor, 't b c -> b c t')
from einops.layers.torch import Rearrange                                            # 沿着某一维复制 output_tensor = repeat(input_tensor, 'h w -> h w c', c=3)
                                            # Rearrange('b c h w -> b (c h w)'),
def pair(t):    #辅助函数，生成元组
    return t if isinstance(t,tuple) else(t,t)
#搭建layernorm层和ffn层。其中fnn主要实现向量的线性尺度变化

#规范化层封装
class preNorm(nn.Module):
    def __init__(self,dim,fn):
        super().__init__()
        self.norm=nn.LayerNorm(dim)
        self.fn=fn
    def forward(self,x,**kwargs):
        return self.fn(self.norm(x),**kwargs)
#FFM层
class FeedForward(nn.Module):
    def __init__(self,dim,hidden_dim,dropout=0.1):
        super().__init__()
        self.net=nn.Sequential(
            nn.Linear(dim,hidden_dim),
            nn.GELU(),
            nn.Dropout(dropout),
            nn.Linear(hidden_dim,dim),
            nn.Dropout(dropout)
        )
    def forward(self,x):
        return self.net(x)

注意力机制实现代码

```python
#注意力机制层
class Attention(nn.Module):
    def __init__(self,dim,heads,dim_heads,dropout=0.1):
        super().__init__()
        inner_dim=dim_heads*heads
        project_out=not(heads ==1 and dim_heads==dim)
        
        self.heads=heads
        self.scale=dim_heads**-0.5
        
        self.attend=nn.Softmax(dim=-1)
        self.to_qkv=nn.Linear(dim,inner_dim*3,bias=False)
        
        self.to_out=nn.Sequential(
         nn.Linear(inner_dim,dim),
         nn.Dropout(dropout)
        ) if project_out else nn.Identity()
        
        
        
    def forward(self,x):
        #注意力系数attention Attention(Q,K,V ) = softmax( QKT√ dk)V
        b, n, _, h = *x.shape, self.heads
        #print('x',x.size())
        qkv=self.to_qkv(x).chunk(3,dim=-1)
        #qkv=torch.tensor([item.detach().numpy() for item in qkv])
        #print('a',qkv.size())
        q,k,v=map(lambda t : rearrange(t,'b n (h d) -> b h n d  ',h=h),qkv)     #q：[batches.heads,num_patches,head_dim=dim/heads]
        #print('q',q.size())
        dots=einsum('b h i d , b h j d -> b h i j',q,k)*self.scale 
        attn=self.attend(dots)
        out=einsum('b h i j, b h j d -> b h i d',attn,v)
        print(out.size())
        out=rearrange(out,'b h n d -> b n (h d)')              #将多头注意力的各个投拼接回到原来的大小dim
        print('out',out.size())
        return self.to_out(out)

将上面组件拼接得到transformer模型

```python
#搭建transformer
class Transformer(nn.Module):
    def __init__(self,dim,depth,heads,dim_head,mlp_dim,dropout=0.1):
        super().__init__()
        self.layers=nn.ModuleList([])
        for _ in range(depth):                                       #多头注意力
            self.layers.append(nn.ModuleList([
            preNorm(dim,Attention(dim,heads=heads,dim_heads=dim_head,dropout=dropout)),
            preNorm(dim,FeedForward(dim,mlp_dim,dropout=dropout))
            ]
            ))
    def forward(self,x):
        for attn,ff in self.layers:
            x=attn(x)+x
            x=ff(x)+x
        return x 

搭建vit模型代码如下：

class ViT(nn.Module):
    def __init__(self,*,image_size,patch_size,num_classes,dim,depth,heads,mlp_dim,pool='cls',channels=3,dim_head,dropout=0.1,emb_dropout=0.1):
        super().__init__()
        image_height,image_width=pair(image_size)
        patch_height,patch_width=pair(patch_size)
        
        assert image_height % patch_height == 0 and patch_height % patch_width == 0
        num_patches=(image_height // patch_height)* (image_width//patch_width)
        patch_dim=channels*patch_height*patch_width                 #ji
        assert pool in {'cls', 'mean'}
        
        #定义块嵌入
        self.to_patch_embedding=nn.Sequential(
              Rearrange('b c (h p1) (w p2) -> b (h w) (p1 p2 c )',p1=patch_height,p2=patch_width),
              nn.Linear(patch_dim,dim),)
        #定义位置编码
        self.pos_embedding=nn.Parameter(torch.randn(1,num_patches+1,dim))
        #定义类别向量
        self.cls_token=nn.Parameter(torch.randn(1,1,dim))
        self.dropout=nn.Dropout(emb_dropout)
        
        self.transformer=Transformer(dim,depth,heads,dim_head,mlp_dim,dropout)
        
        self.pool=pool
        self.to_latent=nn.Identity()
        
        #定义MLP
        self.mlp_head=nn.Sequential(
          nn.LayerNorm(dim),
          nn.Linear(dim,num_classes)
        )
        
    def forward(self,img):
        #块嵌入
        x=self.to_patch_embedding(img)
        b,n,_=x.shape
        #给每个batch(即每张图片）追加类别向量
        cls_tokens=repeat(self.cls_token,'() n d -> b n d ',b=b)
        x=torch.cat((cls_tokens,x),dim=1)  #将类别向量与分块后向量拼接在一起
        #添加位置编码 
        x += self.pos_embedding[:,:(n+1)]  #直接是向量相加 不改变向量大小
        x=self.dropout(x)
        x=self.transformer(x)
        x=x.mean(dim=1) if self.pool == 'mean' else x[:,0]
        
        x=self.to_latent(x)
        #返回mlp后的分类结果
        return self.mlp_head(x)

下面，我们通过输入向量来测试该vit模型的输出
假设输入向量大小为（4,3,224,224)表示batches为4的rgb三通道224*224的图片，vit模型参数如下

#测试该vit模型
images=torch.randn([4,3,224,224])
mymodel=ViT(image_size=224,patch_size=16,num_classes=10,dim=768,depth=2,heads=12,mlp_dim=3072,pool='cls',channels=3,dim_head=64,dropout=0.1,emb_dropout=0.1)

out=mymodel(images)
out.size()

其中的参数表示，输入图片大小为224，patch的大小为16，因此得到（224224/1616）（16163)为196768的向量。transformer特征维度也为768，多头注意力机制取12，depth=2表示重复两个transformer块，mlp隐藏层大小取768.该实例中做的是一个10分类问题。最后得到的输出形状为i（4*10)

最后我们通过torchsummary包来看一看该模型每层的输出大小

summary(mymodel,input_size=(3,224,224))