数据分析案例-基于多元线性回归算法预测学生期末成绩

目录

一、加载数据集

二、数据解读 

三、数据预处理

四.算法应用

4.1线性回归算法 

4.1.1算法介绍

4.1.2算法应用

 4.1.3算法评估和分析

4.2神经网络算法

4.2.1算法简介

4.2.2算法应用

4.2.2算法评估与分析 

4.3随机森林算法

4.3.1算法简介

4.3.2算法应用

 4.3.3算法评估与分析

五.项目总结

---

一、加载数据集

 

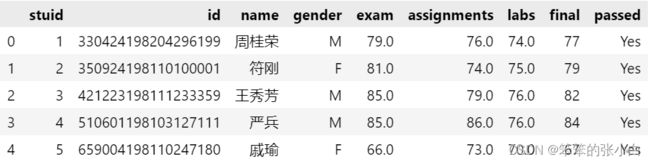
        该数据集包含了不同年级数名学生的科目成绩及一些其它的原始 信息，例如学号、姓名、身份证号等，总成绩由考试成绩、作业成绩、实验成绩等通过一定的规律计算得出。

        首先，导入本次实验用到的第三方库

# 导包
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import warnings
warnings.filterwarnings('ignore')
plt.rcParams['font.sans-serif'] = ['SimHei'] #解决中文显示
plt.rcParams['axes.unicode_minus'] = False   #解决符号无法显示

接着导入数据，并查看数据的前五行

data = pd.read_csv('scores_raw.csv')
data.head() # 查看数据前五行

二、数据解读 

查看数据基本信息

data.info() # 查看数据基本信息

 通过这个结果，我们能看出每个特征的缺失值情况以及每个特征的数据类型

查看数据大小

 通过结果，我们看出原始数据共有86222行，9列数据

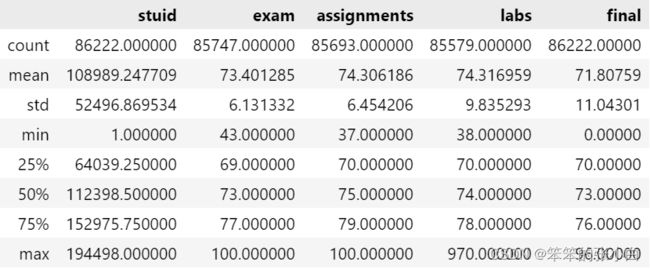
查看数值型数据描述

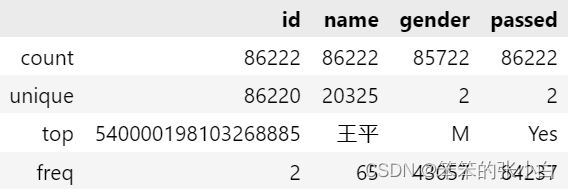
data.describe()  # 查看数值型数据描述

查看非数值型数据描述

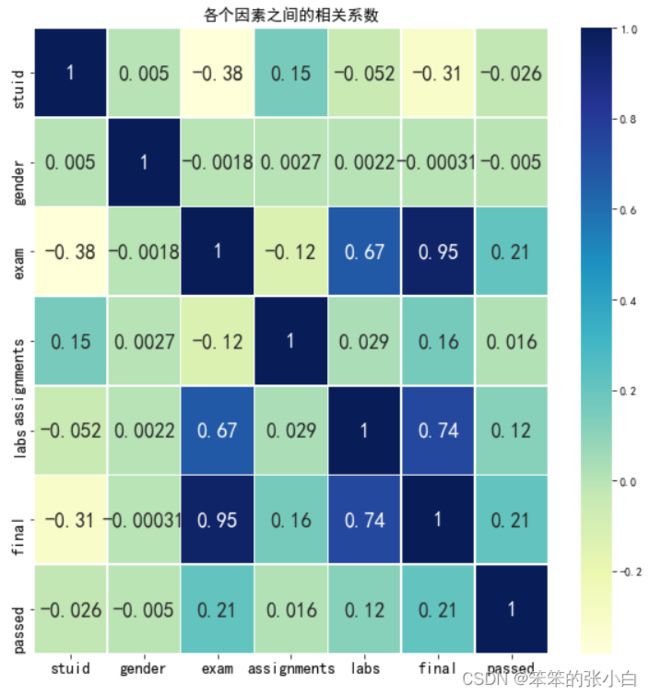
data.describe(include=np.object)  # 查看非数值型数据描述

 

查看各特征之间的相关系数

#相关性
fig = plt.figure(figsize=(10,10))
sns.heatmap(data.corr(),vmax=1,annot=True,linewidths=0.5,cmap='YlGnBu',annot_kws={'fontsize':18})
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.title('各个因素之间的相关系数',fontsize=14)
plt.show()

 

通过上图，我们可以看出每个特征之间的相关系数，从而可以判断特征之间的相关性，其中final和exam的相关性最强，达到0.95. 

三、数据预处理

统计缺失值的个数

 

data.isnull().sum() # 统计缺失值的个数

从结果中，我们可以看到gender,exam,assignment,labs这四列数据都存在缺失值，需要进行缺失值的处理。 

删除缺失值

data.dropna(inplace=True) # 删除缺失值

 这里我们调用dropna()的方法对缺失值进行删除

查看数据是否存在重复值

any(data.duplicated())  # 检验数据是否存在重复值

结果为False，说明数据不存在重复值，反之则存在

查看数据是否存在异常值

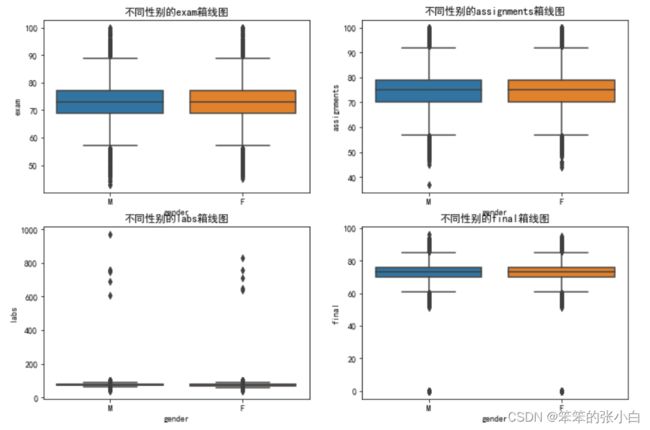
plt.figure(figsize=(12,8))
for i,item in zip(range(1,5),['exam','assignments','labs','final']):
    plt.subplot(2,2,i)
    sns.boxplot(x='gender',y=f'{item}',data=data)
    plt.title(f'不同性别的{item}箱线图')

 通过查看箱线图，我们发现labs这一列数据明显存在异常数据，需要处理

data = data[data['labs']<400]  # 筛选出labs值小于400的
data.reset_index(drop=True,inplace=True)

我们筛选出labs值小于400的数据作为正常数据来进行异常值的处理。

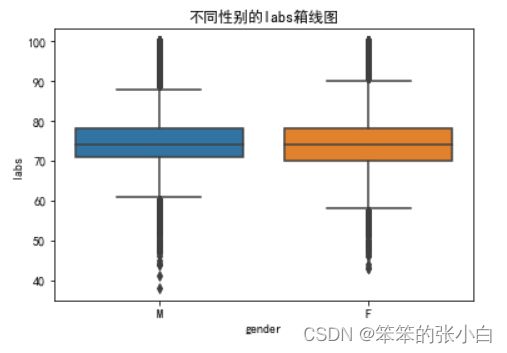
sns.boxplot(x='gender',y='labs',data=data)
plt.title('不同性别的labs箱线图')
plt.show()

处理过异常的labs数据就看起来好多了

对gender和passed这两列数据进行编码处理，便于后面建立模型

data['gender'] = data['gender'].apply(lambda x:0 if x=='F' else 1) # 将男性标记为1，女性标记为0
data['passed'] = data['passed'].apply(lambda x:0 if x=='No' else 1) # 将通过标记为1，不通过标记为0

我们将男性标记为1，女性标记为0；将通过标记为1，不通过标记为0

编码过后的数据，我们就得到了，后面我就开始建立模型

四.算法应用

4.1线性回归算法 

4.1.1算法介绍

一元线性回归是一个主要影响因素作为自变量来解释因变量的变化，在现实问题研究中，因变量的变化往往受几个重要因素的影响，此时就需要用两个或两个以上的影响因素作为自变量来解释因变量的变化，这就是多元回归亦称多重回归。当多个自变量与因变量之间是线性关系时，所进行的回归分析就是多元线性回归。 　设y为因变量X1,X2…Xk为自变量，并且自变量与因变量之间为线性关系时，则多元线性回归模型为：

Y=b0+b1x1+…+bkxk+e

其中，b0为常数项，b1,b2…bk为回归系数，b1为X1,X2…Xk固定时，x1每增加一个单位对y的效应，即x1对y的偏回归系数；同理b2为X1,X2…Xk固定时，x2每增加一个单位对y的效应，即，x2对y的偏回归系数，等等。如果两个自变量x1,x2同一个因变量y呈线相关时，可用二元线性回归模型描述为：

y=b0 +b1x1 +b2x2 +e

建立多元线性回归模型时，为了保证回归模型具有优良的解释能力和预测效果，应首先注意自变量的选择，其准则是：

(1)自变量对因变量必须有显著的影响，并呈密切的线性相关；

(2)自变量与因变量之间的线性相关必须是真实的，而不是形式上的；

(3)自变量之间应具有一定的互斥性，即自变量之间的相关程度不应高于自变量与因变量之间的相关程度；

(4)自变量应具有完整的统计数据，其预测值容易确定。

4.1.2算法应用

 这里，我们建立多元线性回归的模型，并通过预测值计算出模型的MSE值为0.0837

 4.1.3算法评估和分析

 通过模型结果，我们得出模型的最佳拟合线的截距为-0.4399，回归系数为[0.0042404 0.69913402 0.1997178 0.09988155 0.06349992]

4.2神经网络算法

4.2.1算法简介

神经网络（Neural Networks,NN）是由大量的、简单的处理单元（称为神经元）广泛地互相连接而形成的复杂网络系统，它反映了人脑功能的许多基本特征，是一个高度复杂的非线性动力学习系统。神经网络具有大规模并行、分布式存储和处理、自组织、自适应和自学能力，特别适合处理需要同时考虑许多因素和条件的、不精确和模糊的信息处理问题。神经网络的发展与神经科学、数理科学、认知科学、计算机科学、人工智能、信息科学、控制论、机器人学、微电子学、心理学、光计算、分子生物学等有关，是一门新兴的边缘交叉学科。

神经网络的基础在于神经元。

神经元是以生物神经系统的神经细胞为基础的生物模型。在人们对生物神经系统进行研究，以探讨人工智能的机制时，把神经元数学化，从而产生了神经元数学模型。

大量的形式相同的神经元连结在—起就组成了神经网络。神经网络是一个高度非线性动力学系统。虽然，每个神经元的结构和功能都不复杂，但是神经网络的动态行为则是十分复杂的；因此，用神经网络可以表达实际物理世界的各种现象。

神经网络模型是以神经元的数学模型为基础来描述的。人工神经网络(ArtificialNuearlNewtokr)s,是对人类大脑系统的一阶特性的一种描。简单地讲,它是一个数学模型。神经网络模型由网络拓扑．节点特点和学习规则来表示。神经网络对人们的巨大吸引力主要在下列几点：

1．并行分布处理。

2．高度鲁棒性和容错能力。

3．分布存储及学习能力。

4．能充分逼近复杂的非线性关系。

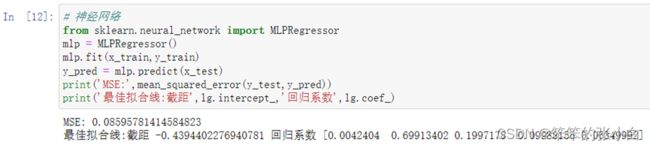
4.2.2算法应用

这里，我们建立神经网络的模型，并通过预测值计算出模型的MSE值为0.0859 

4.2.2算法评估与分析 

 通过模型结果，我们得出模型的最佳拟合线：截距 -0.4394402276940781 回归系数 [0.0042404 0.69913402 0.1997178 0.09988155 0.06349992]

4.3随机森林算法

4.3.1算法简介

随机森林是一种有监督学习算法。就像它的名字一样，它创建了一个森林，并使它拥有某种方式随机性。所构建的“森林”是决策树的集成，大部分时候都是用“bagging”方法训练的。bagging 方法，即 bootstrapaggregating，采用的是随机有放回的选择训练数据然后构造分类器，最后组合学习到的模型来增加整体的效果。简而言之，随机森林建立了多个决策树，并将它们合并在一起以获得更准确和稳定的预测。其一大优势在于它既可用于分类，也可用于回归问题，这两类问题恰好构成了当前的大多数机器学习系统所需要面对的。

随机森林分类器使用所有的决策树分类器以及 bagging 分类器的超参数来控制整体结构。与其先构建 bagging分类器，并将其传递给决策树分类器，我们可以直接使用随机森林分类器类，这样对于决策树而言，更加方便和优化。要注意的是，回归问题同样有一个随机森林回归器与之相对应。

随机森林算法中树的增长会给模型带来额外的随机性。与决策树不同的是，每个节点被分割成最小化误差的最佳指标，在随机森林中我们选择随机选择的指标来构建最佳分割。因此，在随机森林中，仅考虑用于分割节点的随机子集，甚至可以通过在每个指标上使用随机阈值来使树更加随机，而不是如正常的决策树一样搜索最佳阈值。这个过程产生了广泛的多样性，通常可以得到更好的模型。

4.3.2算法应用

这里，我们建立神经网络的模型，并通过预测值计算出模型的MSE值为0.0118 

 4.3.3算法评估与分析

 

 通过随机森林模型得出的重要特征中，我们可以看出影响final这一列数据的特征中，exam的影响最大，其次是assignments

五.项目总结

通过这次Python项目实战，我学到了许多新的知识，这是一个让我把书本上的理论知识运用于实践中的好机会。原先，学的时候感叹学的资料太难懂，此刻想来，有些其实并不难，关键在于理解。

在这次实战中还锻炼了我其他方面的潜力，提高了我的综合素质。首先，它锻炼了我做项目的潜力，提高了独立思考问题、自我动手操作的潜力，在工作的过程中，复习了以前学习过的知识，并掌握了一些应用知识的技巧等

在此次实战中，我还学会了下面几点工作学习心态：

1）继续学习，不断提升理论涵养。在信息时代，学习是不断地汲取新信息，获得事业进步的动力。作为一名青年学子更就应把学习作为持续工作用心性的重要途径。走上工作岗位后，我会用心响应单位号召，结合工作实际，不断学习理论、业务知识和社会知识，用先进的理论武装头脑，用精良的业务知识提升潜力，以广博的社会知识拓展视野。

2）努力实践，自觉进行主角转化。只有将理论付诸于实践才能实现理论自身的价值，也只有将理论付诸于实践才能使理论得以检验。同样，一个人的价值也是透过实践活动来实现的，也只有透过实践才能锻炼人的品质，彰显人的意志。

3）提高工作用心性和主动性。实习，是开端也是结束。展此刻自我面前的是一片任自我驰骋的沃土，也分明感受到了沉甸甸的职责。在今后的工作和生活中，我将继续学习，深入实践，不断提升自我，努力创造业绩，继续创造更多的价值。

这次Python实战不仅仅使我学到了知识，丰富了经验。也帮忙我缩小了实践和理论的差距。在未来的工作中我会把学到的理论知识和实践经验不断的应用到实际工作中，为实现理想而努力。