【抽样技术】CH2 简单随机抽样
目录
前言
一、定义
二、概述
1.总体
2.单元
3.抽样比
4.样本抽取原则
5.在抽样理论中的地位与作用
三、参数估计
1.参数表示
2.对总体特征的估计思路
3.对总体均值的估计
(1)引理
(2)对总体均值的估计
4.方差和协方差的估计
5.区间估计
6.样本量的确定
(1)费用
(2)步骤
(3)精度(编辑 编辑 编辑)
(4)估计总体均值时样本量的确定方法
7.对总体比例的估计
(1)总体比例的估计量
(2)总体比例估计量的方差
(3)估计总体比例时样本量的确定
8.总体总值的简单估计
(1)总体总值的简单估计
(2)总体总值简单估计量的性质
(3)估计总体总值时估计量的确定
9.放回简单随机抽样的估计
10.设计效应( )
(1)定义
(2)的作用
(3)设计效应和样本量的确定
四、附表——抽样理论&数理统计的比较
前言
学习一种抽样方法必须掌握的五个要点:
- 该抽样方法的定义
- 实施抽样的方法
- 利用该抽样方法所得数据进行参数估计的方法
- 估计量的性质:期望、方差
- 估计量方差(精度)的估计方法
一、定义
1.从总体的![]() 个单元中,一次整批抽取
个单元中,一次整批抽取![]() 个单元,使任何一个单元被抽中的概率都相等,任何n个不同单元组成的组合被抽中的概率也都相等,这种抽样成为简单随机抽样(s.r.s)。
个单元,使任何一个单元被抽中的概率都相等,任何n个不同单元组成的组合被抽中的概率也都相等,这种抽样成为简单随机抽样(s.r.s)。
2.从总体的![]() 个单元中,逐个不放回地抽取单元,每次抽到尚未入样的任何一个单元的概率都相等,直到抽足
个单元中,逐个不放回地抽取单元,每次抽到尚未入样的任何一个单元的概率都相等,直到抽足![]() 个单元为止,这样所得的
个单元为止,这样所得的![]() 个单元组成一个简单随机样本。(现实中采用的方法)
个单元组成一个简单随机样本。(现实中采用的方法)
【注】
- 对于简单随机抽样,依次抽到一组特定样本单元的概率为:
![]()
之前课本中![]() 为
为![]() ,
,![]() 为其具体值(非随机);在抽样课程中,
为其具体值(非随机);在抽样课程中,![]() 为总体真值(非随机),
为总体真值(非随机),![]() 为样本值,是
为样本值,是![]() 。前面提到的
。前面提到的![]() 一般较大,若从
一般较大,若从![]() 种可能的样本中随机抽取一种,需要先列出所有可能的
种可能的样本中随机抽取一种,需要先列出所有可能的![]() 种样本,不现实。
种样本,不现实。
- 不考虑顺序,则抽中一组特定样本的概率为:
- 对于样本量n=1和n=2两种特殊情形(N个总体单元中抽取n个样本单元的简单随机抽样)
![]() ,
,![]()
![]()
![]()
不计第几次抽样,抽中某特定单元的概率相等,都为![]() 。
。
二、概述
1.总体
- 具体总体
- 有限总体
- 与抽样框存在一一对应关系的实际调查总体
2.单元
构成抽样总体的抽样单元并不总是等同于个体,个体是不可再分的单元,抽样单元可能包含很多个体。
3.抽样比
样本容量![]() 相对于总体规模
相对于总体规模![]() 的比例
的比例![]() 。
。
4.样本抽取原则
- 排除主观因素,按随机原则取样
- 每个抽样单元被抽中的概率都是已知或事先可以计算的
- 总体各单元的入样概率相等
- 对于不放回抽样,总体各单元的入样概率之和等于样本量

5.在抽样理论中的地位与作用
优点:
- 简单直观、理论成熟
- 抽样调查的基础
缺点:
- N很大时难以获得抽样框
- 样本分散时不易实施
- 很少单独使用,除非没有其他信息(常结合其他抽样方法使用)
三、参数估计
1.参数表示
| 总体真值 | 样本值 |
| 示性变量 |
|
【注】总体参数上面带符号“^”表示由样本得到的总体参数的估计。估计量的方差用大写的![]() 表示,对
表示,对![]() 的样本估计值用
的样本估计值用![]() 表示。
表示。
2.对总体特征的估计思路
- 利用样本的目标变量观测值对其总体参数进行直接估计
- 借助与目标变量高度相关的辅助变量对目标变量总体参数进行区间估计,如比率估计、回归估计等
3.对总体均值的估计
(1)引理
![]()
【注】简单随机抽样下,所有可能的![]() 个样本中,包含某个特点单元的样本数为?同时包含两个特定不同单元的样本数为?
个样本中,包含某个特点单元的样本数为?同时包含两个特定不同单元的样本数为?
(2)对总体均值的估计
【定理2.1】对于简单随机抽样,![]() 是
是![]() 的无偏估计(估计量无偏性),即
的无偏估计(估计量无偏性),即![]()
证明:从总体规模为N的总体中抽取一个样本量为n的简单随机样本。 若对总体中的每个单元![]() ,引入随机变量
,引入随机变量![]() ,如下,
,如下,![]() ,1表示
,1表示![]() 被抽中,0表示未被抽中。则
被抽中,0表示未被抽中。则![]() 可表达为
可表达为 ,式中
,式中![]() 是常数,故
是常数,故
【推论2.1】对于简单随机抽样,![]() 的期望为
的期望为![]()
【推论2.2】对于简单随机抽样,![]() 的期望为
的期望为![]()
【推论2.3】对于简单随机抽样,n较大时,![]() 的期望为
的期望为![]()
【定理2.2】对于简单随机抽样,![]() 的方差
的方差![]() ,式中
,式中![]() 为抽样比,
为抽样比,![]() 为有限总体校正系数(fpc)
为有限总体校正系数(fpc)
![]()
【注】简单估计量估计精度影响因素![]() 。估计量的方差
。估计量的方差![]() 是衡量估计量精度的度量。影响估计量方差的因素包括样本量
是衡量估计量精度的度量。影响估计量方差的因素包括样本量![]() ,总体大小
,总体大小![]() 和总体方差
和总体方差![]() 。通常N很大,当
。通常N很大,当![]() 时,可将
时,可将![]() 近似取为1。总体方差是我们无法改变的,因此在简单随机抽样的条件下,只有通过加大样本量来提高估计量的精度。
近似取为1。总体方差是我们无法改变的,因此在简单随机抽样的条件下,只有通过加大样本量来提高估计量的精度。
4.方差和协方差的估计
![]()
![]()
5.区间估计
由中心极限定理,![]() ,
,。总体均值的置信区间为
![]() ,其中
,其中![]() 是标准正态分布的上
是标准正态分布的上![]() 分位数,
分位数,![]() 称为绝对误差限。用
称为绝对误差限。用![]() 估计
估计![]() ,因而
,因而![]() 的置信区间为
的置信区间为![]() 。进行多次抽样后,根据各次的样本算得的置信区间包含总体均值
。进行多次抽样后,根据各次的样本算得的置信区间包含总体均值![]() 的比例约为
的比例约为![]() 。
。![]() 称为置信水平或置信度,反应抽样调查的信度水平。绝对误差限
称为置信水平或置信度,反应抽样调查的信度水平。绝对误差限![]() 为置信区间的半长。
为置信区间的半长。
![]() 的估计:
的估计:![]() ,
,![]() 的估计:
的估计:![]() 。
。
6.样本量的确定
(1)费用
![]() 。即总费用=固定费用+可变费用。固定费用包含设计费、分析费、办公费、管理费、场租费……;
。即总费用=固定费用+可变费用。固定费用包含设计费、分析费、办公费、管理费、场租费……;![]() ,即平均调查一个样本单元的费用包括访问员费、交通费、礼品费、电话费……
,即平均调查一个样本单元的费用包括访问员费、交通费、礼品费、电话费……
(2)步骤
- 明确估计量的精度要求(绝对误差限
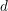 或相对误差限
或相对误差限 )
) - 找出样本量与精度之间的关系
- 估计所需的样本量数值,即求解

- 如超出预算,调整精度值重新计算样本量
(3)精度(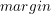
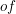
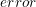 )
)
(4)估计总体均值时样本量的确定方法
- 按绝对误差限确定样本量
设在![]() 置信度下,给定绝对误差限为
置信度下,给定绝对误差限为![]() ,即
,即![]() ,得出
,得出![]() ,N很大时,
,N很大时,![]() 。其中,
。其中,![]() 为有放回抽样或无限总体条件下达到该精度至少需要的样本量。
为有放回抽样或无限总体条件下达到该精度至少需要的样本量。
- 按相对误差限确定样本量
7.对总体比例的估计
估计具有某类特征的单元占总体单元数N中的比例P。
将总体单元按是否具有这种特征划分为两类,设总体中有A个单元具有这个特征,如果对每个单元都定义指标值![]() ,1表示第
,1表示第![]() 个单元具有所考虑的特征。
个单元具有所考虑的特征。![]() 。
。
(1)总体比例的估计量
总体比例![]() 的估计量为样本比例
的估计量为样本比例![]() ,其中
,其中![]() ,1表示第
,1表示第![]() 个单元具有所考虑的特征。
个单元具有所考虑的特征。
样本比例![]() 是总体比例
是总体比例![]() 的无偏估计。
的无偏估计。![]()
(2)总体比例估计量的方差
总体比例的估计量![]() 的方差
的方差![]() 。
。
![]()
(3)估计总体比例时样本量的确定
当待估参数是![]() 时,估计量是
时,估计量是![]() 。
。
- 给定
 的绝对误差限
的绝对误差限
![]()
![]() 为放回抽样或无限总体情形下达到该精度最少所需样本量
为放回抽样或无限总体情形下达到该精度最少所需样本量
8.总体总值的简单估计
总体总值为总体均值的N倍,即 ,只要有了总体均值的估计结果,就可以很容易地推出总体总值的估计结果。
,只要有了总体均值的估计结果,就可以很容易地推出总体总值的估计结果。
(1)总体总值的简单估计
N倍的样本均值是总体总值的简单估计量,即![]() 。
。
(2)总体总值简单估计量的性质
由于总体总值是总体均值的N倍,其简单估计量也是总体均值估计量的N倍,而N是固定常数,所以总体总值的简单估计量的性质由总体均值的简单估计量的性质来决定。
容易证明:
![]()
(3)估计总体总值时估计量的确定
![]()
9.放回简单随机抽样的估计
现实中有许多情况下,抽样是放回的,即从总体中抽中的单元每次都要放回总体中去。例如在城市中对行人、车辆的调查等抽样都是有放回的,有可能重复抽中某些单位。
对于每次抽到的结果(视为随机变量)![]() 都有
都有
10.设计效应(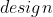
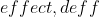 )
)
(1)定义
所采用抽样技术的参数估计量方差与相同样本量下简单随机抽样的参数估计量方差之比。
- 值越大,说明估计效率越低
(2)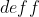 的作用
的作用
- 评价抽样设计的一个依据
如果![]() ,则抽样设计比简单随机抽样的效率高
,则抽样设计比简单随机抽样的效率高
如果![]() ,则抽样设计比简单随机抽样的效率低
,则抽样设计比简单随机抽样的效率低
- 计算样本量
如多阶段抽样的![]() 大约在
大约在![]() 之间。
之间。![]() ,
,![]() 为简单随机抽样下满足估计量精度要求所需样本量。
为简单随机抽样下满足估计量精度要求所需样本量。
(3)设计效应和样本量的确定
所以,要满足一定的估计精度,采用放回简单随机抽样比采用不放回简单随机抽样需要更大的样本量。
![]() 常用于复杂抽样样本量的确定;在一定精度条件下,简单随机抽样所需的样本量
常用于复杂抽样样本量的确定;在一定精度条件下,简单随机抽样所需的样本量![]() 比较容易得到。
比较容易得到。
所考虑的抽样设计的样本量=简单随机抽样时满足方差要求时的样本量*![]()
![]()
四、附表——抽样理论&数理统计的比较
| 抽样理论 | 数理统计 | |
| 假设 | 有限总体,样本之间不独立有 |
无限总体,样本之间独立,可取无限种可能的样本 |
| 符号 | ||
| 定义 |  |
 |
| 期望 | ![E(\bar{y})=E(\frac{1}{n}\sum_{i=1}^{n})=\frac{1}{n}\sum_{i=1}^{n}E(y_{i})=\frac{1}{n}[n\mu ]=\mu](http://img.e-com-net.com/image/info8/cada301f51334f2ea11900ee86f2963d.gif) |
![E(\bar{y})=E(\frac{1}{n}\sum_{i=1}^{n})=\frac{1}{n}\sum_{i=1}^{n}E(y_{i})=\frac{1}{n}[n\mu ]=\mu](http://img.e-com-net.com/image/info8/cada301f51334f2ea11900ee86f2963d.gif) |
| 方差 | ![V(\bar{y})=E[\bar{y}_{i}-\mu ]=E[\frac{1}{n}\sum_{i=1}^{n}-\mu ]=\frac{1}{n}{E(y_{i}-\mu )}^2=\frac{\sigma ^2}{n}](http://img.e-com-net.com/image/info8/7a68de159e1849d49e9a45acbfb5d625.gif) |
| 抽样 理论 & 数理 统计 |
相同之处 | 不同之处 |
| 定义 | 都是根据从一个总体中 抽样得到的样本,然后 定义样本均值为: |
抽样理论中样本是从有限总体中按不放回的抽样方法得到的,样本中的样本点不会重复; 数理统计中的样本是从无限总体中利用有放回的抽样方法得到的,样本点有可能是重复的。 |
| 性质 | (1)样本均值的期望都等于总体均值,也就是抽样理论和数理统计中的样本均值都是无偏估计 (2)不论总体原来是何种分布,在样本量足够大的条件下,样本均值近似服从正态分布 |
(1)抽样理论中,各个样本之间是不独立的;数理统计中的各个样本之间是相互独立的 |
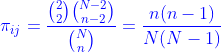



![\left [ p-{u_{\frac{\alpha }{2}}\sqrt{\frac{(1-f)pq}{n-1}}} , p+{u_{\frac{\alpha }{2}}\sqrt{\frac{(1-f)pq}{n-1}}}\right ]](http://img.e-com-net.com/image/info8/b1e04b0f5c6d4796b8b298270d4d3f58.gif)




