深度学习（9）——暂退法（Dropout）

前言

我们再回顾一下过拟合的问题，过拟合就是模型对训练样本训练的过于好，但是用在测试样本上准确率却出现特别差的情况。
造成过拟合的情况大致分为3类：

• 权重值的范围太大，导致模型极其不稳定
• 对于简单的数据选取的模型过于复杂，比如隐藏层过多，隐藏层的神经元过多
• 训练样本过少，导致模型对少样本完全拟合，对于新样本极其陌生

在上一篇blog里讲了个权重衰退的方法，这个方法就是针对情况1提出的解决方案，该方案对损失函数作了处理，新的损失函数在原有的损失函数后面加上了一个L2正则，这可以使得模型在做梯度下降时，使得每次的权重值相比原来下降的更多一些，可以有效的使得最后的权重值收缩的比较小，解决过拟合的问题。
但这个方案现在用的不是很多，实际上我们在碰到一个样本的时候，一开始选取的模型肯定无法保证是最优模型的，可能过深或者过浅，只有在多次调试，调整超参数才能使得模型容量变得比较合适，导致过拟合的主要原因还是出在模型复杂度的调整上，因此本文提供了一个方法可以方便我们调整模型复杂度，该方法可以减少隐藏神经元个数同时对整个神经网络不产生影响。

原理介绍

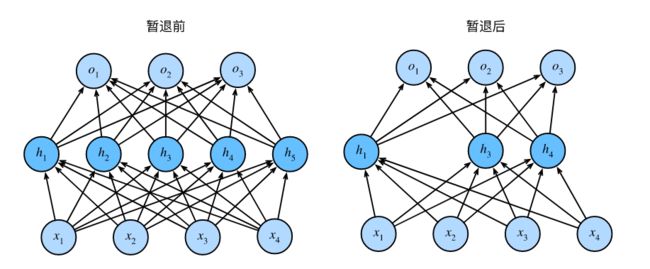
这是之前多层感知机用到的神经网络，4维输入，3维输出，隐藏层5个神经元的结构，实际上我们回到前言里讲的话题，由于样本都是已知的，想要解决什么样的问题也是已知的，因此输入层和输出层神经元个数肯定就是固定的，那么想优化模型只能从隐藏层入手对吧，好我们接着讲dropout怎么优化模型。
dropout就是给出一个概率p，比方说p=40%，那么就是说40%的隐藏层神经元要被删掉，只留下60%的神经元，那么这是我们表面理解，对于程序来说，就是将这40%的神经元赋值0，那么可以想一下一个神经元等于0了，那么他对下一层还能产出结果吗，0乘多少权重都是0，相当于这个被dropout选中的神经元没价值了，那他就相当于被删了。
那么接下来还有一个问题，40%神经元赋值0相当于删掉，那么剩余60%神经元如何能表达原有的这一层隐藏层呢，那么就要用到这里的一个dropout算法了。

原来的每个神经元代表的数就是h，dropout后的就是h‘。那么概率为p的神经元赋值0，概率为1-p的神经元赋值为h/1-p。这样的改变最终可以使得dropout后的隐藏层期望和原有期望一致。
E（h’）=h
因为E（h‘）=p0+(1-p)(h/1-p)=h

实现方法

导包

import torch
from torch import nn
from d2l import torch as d2l

dropout实现

def dropout_layer(X, dropout):
	#dropout指的就是多少概率的神经元被删
	#因此概率必须在0-1，不在这范围就报错
    assert 0 <= dropout <= 1
    # 在本情况中，所有元素都被丢弃
    if dropout == 1:
        return torch.zeros_like(X)
    # 在本情况中，所有元素都被保留
    if dropout == 0:
        return X
    #随机出X.shape长度的随机数,范围是【0，1）
    mask = (torch.rand(X.shape) > dropout).float()
    return mask * X / (1.0 - dropout)

这个函数里最后两句代码，我举例解释一下：
torch.rand（size）就是返回size个范围为【0，1）的数。torch.rand（10）就是返回10个范围为【0，1）的数，这里X.shape就是隐藏层神经元个数。然后就是这10个数挨个和dropout这个概率值去比较，比方说第一个数比dropout大的就是true对吧，true格式转换后就是1，那么第一个位置的mask标记就是1，也就是说他是一个要保留下来的神经元，那么就对他作X/1-dropout。那么第二个位置的数比dropout小就是false对吧，格式转换后是不是0，然后第二个位置的mask标记就是0，那么0*后面那一堆反正肯定是0嘛，那么就相当于第二个神经元删了，就是那么回事情。
实际上这个代码看上去好简单，但理解起来又好绕，写个简单的循环语句，if语句好理解一点不好嘛，代码可读性强一点不也是一个重要因素嘛。但实际上，代码更重要的是运行的开销，时间的花费，这样写代码实际上开销其实会小一些，深度学习通常就是跑的时间会长，那么你代码每一处细节让他开销小一点对整个模型训练还是会省去不少时间的。
下面举了几个例子

X= torch.arange(16, dtype = torch.float32).reshape((2, 8))
print(X)
print(dropout_layer(X, 0.))
print(dropout_layer(X, 0.5))
print(dropout_layer(X, 1.))

tensor([[ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.],
        [ 8.,  9., 10., 11., 12., 13., 14., 15.]])
tensor([[ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.],
        [ 8.,  9., 10., 11., 12., 13., 14., 15.]])
tensor([[ 0.,  0.,  4.,  6.,  0., 10., 12.,  0.],
        [ 0.,  0.,  0., 22., 24.,  0.,  0.,  0.]])
tensor([[0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0.]])

定义模型

这里还是用了使用多层感知机来做图像分类问题，输入层784，输出层10，2层隐藏层，每层神经元个数都是256个。
dropout1就是第一层神经元要去除20%的神经元；
dropout2就是第一层神经元要去除50%的神经元。
这里使用的风格和之前不太一样，不过更规范一些了，因为他是4层网络，所以就是有3个全连接的结构，也就是lin1-3。然后前两个全连接层是需要用relu函数的，最后一个往输出层输出的不需要relu函数。然后这两层也要用暂退法处理一下。

num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256

dropout1, dropout2 = 0.2, 0.5

class Net(nn.Module):
    def __init__(self, num_inputs, num_outputs, num_hiddens1, num_hiddens2,
                 is_training = True):
        super(Net, self).__init__()
        self.num_inputs = num_inputs
        self.training = is_training
        self.lin1 = nn.Linear(num_inputs, num_hiddens1)
        self.lin2 = nn.Linear(num_hiddens1, num_hiddens2)
        self.lin3 = nn.Linear(num_hiddens2, num_outputs)
        self.relu = nn.ReLU()

    def forward(self, X):
        H1 = self.relu(self.lin1(X.reshape((-1, self.num_inputs))))
        # 只有在训练模型时才使用dropout
        if self.training == True:
            # 在第一个全连接层之后添加一个dropout层
            H1 = dropout_layer(H1, dropout1)
        H2 = self.relu(self.lin2(H1))
        if self.training == True:
            # 在第二个全连接层之后添加一个dropout层
            H2 = dropout_layer(H2, dropout2)
        out = self.lin3(H2)
        return out

#这里NET（）相当于调用了里面的forward方法
net = Net(num_inputs, num_outputs, num_hiddens1, num_hiddens2)

训练与测试

这里和前面MLP那章一样，其实这篇blog唯一不同的就是对模型搞了给dropout

num_epochs, lr, batch_size = 10, 0.5, 256
loss = nn.CrossEntropyLoss(reduction='none')
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
trainer = torch.optim.SGD(net.parameters(), lr=lr)
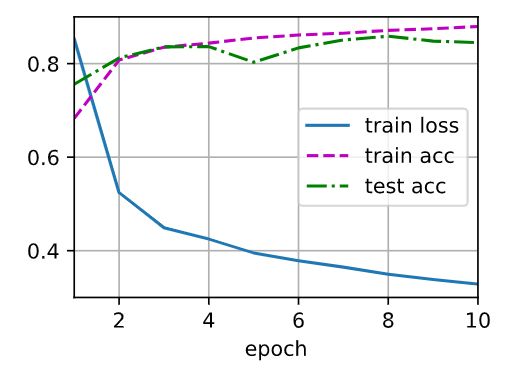
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

简洁实现

net = nn.Sequential(nn.Flatten(),
        nn.Linear(784, 256),
        nn.ReLU(),
        # 在第一个全连接层之后添加一个dropout层
        nn.Dropout(dropout1),
        nn.Linear(256, 256),
        nn.ReLU(),
        # 在第二个全连接层之后添加一个dropout层
        nn.Dropout(dropout2),
        nn.Linear(256, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

这里看到框架多方便了吧，上一章我们用权重衰退，加个weightout变量就实现了，这里加个nn.dropout就实现了，这里按照神经网络的顺序来弄就行，第一层全连接层，然后激活函数，然后暂退法，然后第二层，比较方便。

小结

暂退法为我们提供了一种很好的解决过拟合的方法，在现代的MLP算法中，我们也经常用Dropout来降低模型复杂度，来优化模型。