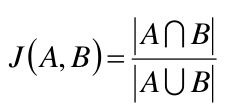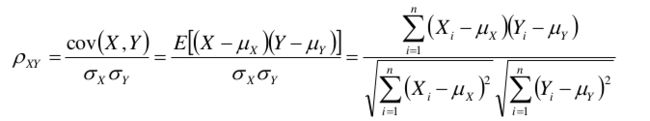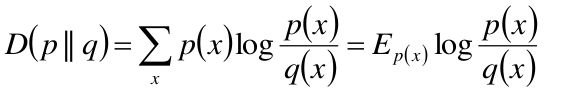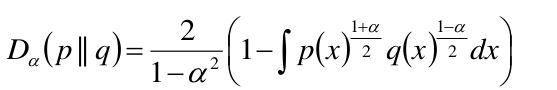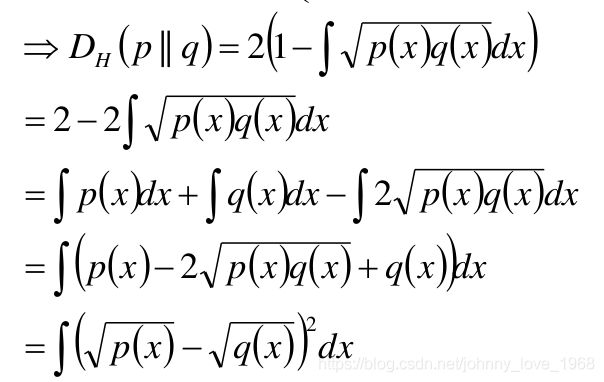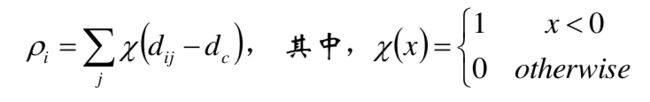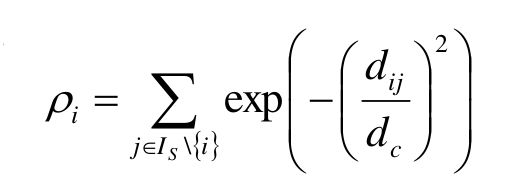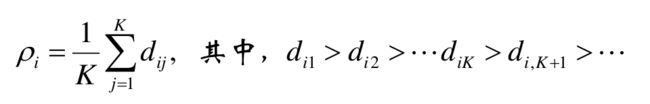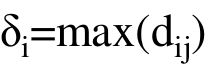聚类算法简介

聚类

一.什么是聚类

1.聚类定义

聚类就是对大量未知标注的数据集,按数据的内在相似性将数据集划分为多个类别,使类别内的数据相似度较大而类别间的数据相似度较小。由这个定义，我们便可以知道，数据集并没有目标值。因此聚类算法属于无监督算法。

2. 相似度的衡量

之前在k-means算法的简介当中，提及过一个欧式距离。但实际上，相似度的衡量方式有很多种。比如说：

• 欧式距离（这里列出的是欧式距离的拓展，闵可夫斯基距离）：

• 杰卡德相似系数(Jaccard)

• 余弦相似度：
  $$\cos (\theta )=\frac{x^{T}y}{|x|\cdot |y|}$$
  这个是x向量与y向量之间的夹角为theta。如果x，y都是多维呢？如下：

• Pearson相似系数：

• 相对熵(K-L距离)：

• Hellinger距离：

在Hellinger距离当中，特殊的，我们取a=0的时候：

对于这几种距离到底适用于哪种场景，优缺点是什么，其实很难说，查了一些资料，一句话引起了我的注意：

其实你会发现，选择不同的相似性度量方法，对结果的影响是微乎其微的。 ——《集体智慧编程》

3. 聚类与降维的关系

我们看下面这个示例，我们假设有x1,x2, ……, xn堆样本，每堆样本有m个数据，那么这m个堆样本就组成了n*m的矩阵。
$$\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\\ .\\ .\\ .\\ .\\ x_n\end{array}\right)\Rightarrow \left(\begin{array}{ccccccc}{x}_1^{(1)}& & x_1^{(2)}& & \dots \dots & & x_1^{(m)}\\ x_2^{(1)}& & x_2^{(2)}& & \dots \dots & & x_2^{(m)}\\ x_3^{(1)}& & x_3^{(2)}& & \dots \dots & & x_3^{(m)}\\ \dots \dots & & \dots \dots & & \dots \dots & & \dots \dots \\ \dots \dots & & \dots \dots & & \dots \dots & & \dots \dots \\ \dots \dots & & \dots \dots & & \dots \dots & & \dots \dots \\ x_n^{(1)}& & x_n^{(2)}& & \dots \dots & & x_n^{(m)}\end{array}\right)$$

聚类，就是要把这些样本进行分类，是一种无监督的分类。那么，经过分类之后，发现整体有k=6个簇。依据不同的簇，又可以组成一个m*6的one-hot矩阵如下：

$$\left(\begin{array}{ccccccc}{x}_1^{(1)}& & x_1^{(2)}& & \dots \dots & & x_1^{(m)}\\ x_2^{(1)}& & x_2^{(2)}& & \dots \dots & & x_2^{(m)}\\ x_3^{(1)}& & x_3^{(2)}& & \dots \dots & & x_3^{(m)}\\ \dots \dots & & \dots \dots & & \dots \dots & & \dots \dots \\ \dots \dots & & \dots \dots & & \dots \dots & & \dots \dots \\ \dots \dots & & \dots \dots & & \dots \dots & & \dots \dots \\ x_n^{(1)}& & x_n^{(2)}& & \dots \dots & & x_n^{(m)}\end{array}\right)\Rightarrow (one\_hot矩阵)\Rightarrow n\ast 6矩阵$$

这就是一种降维。所以在某些情景里面，降维和聚类具有一定的相通的地方。

4.聚类的思想

基本思想:对于给定的类别数目k,首先给出初始划分,通过迭代改变样本和簇的隶属关系,使得每一次改进之后的划分方案都较前一次好

二.K-means算法

这个，先看一看简介：k-means算法简介
这个之前有介绍过基本原理，但是需要做一些补充

1. 算法步骤

假定输入样本为S=x 1 ,x 2 ,…,x m ,则 算法步骤为:

• 选择初始的k个类别中心μ1, μ2 … μk

• 对于每个样本xi ,将其标记为距离类别中心最近的类别,即:
  $$labe{l}_i=argmi{n}_{1<=j<=k}||x_i-u_j||$$

• 将每个类别中心更新为隶属该类别的所有样本的均值
  $${\mu }_j=\frac{1}{|c_j|}\sum _{i\in c_j}{x}_i$$

• 重复最后两步,直到类别中心的变化小于某阈值。

中止条件：迭代次数/簇中心变化率/最小平方误差MSE(Minimum Squared Error)，这个需要你自己指定

2. k-means公式化解读

其实，对于k-means算法，和之前的机器学习算法一样，也有一个目标函数，我们假设有K个簇中心为 u1 , u2 , …… , uk ,每个簇的样本数目为 N1 , N2 , …… , Nk，我们使用平方误差做目标函数，就会得到如下公式：

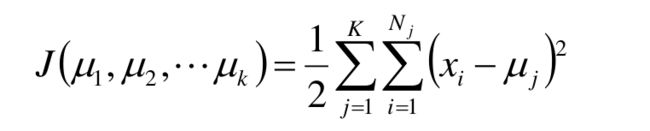
如何理解这个损失函数呢？

我们假定有三个类别，分别服从三个不同的正态分布N(u1, a1^2), N(u2, a2^2), N(u3, a3^2)。分别求这三个类别里面，所有样本的最大似然估计。以第一个类别为例：
$$x^{(i)}\sim N(u1,{\sigma }_1^2)\sim \frac{1}{\sqrt{2\pi }{\sigma }_1}{e}^{-\frac{(x^{(i)}-u1{)}^2}{2\sigma 1^2}}$$

第一个类别里面的所有样本都是服从这样一个分布，我们按照求最大似然估计的套路，先累乘，就是：
$$\prod _{i=1}^n\frac{1}{\sqrt{2\pi }{\sigma }_1}{e}^{-\frac{(x^{(i)}-u1{)}^2}{2\sigma 1^2}}$$
那么，三个类别我们都进行累乘，然后取对数。前面带有pi的系数是常量，可以不管，最后剩下的就是xi-uj。

通过上述这个推导，有没有想过这样一个事情，为什么正态分布的情况竟然能够和损失函数完美对接呢？由此，也可以大体猜出一件事情：k-means对样本分布是有一定的要求的，即：整体符合正态分布。即使单个样本不一定是服从于正态分布，但如果样本足够大，那么通过大数定律，使得整体大概符合正态分布也是可以的。

如果针对这个损失函数，我们对不同的中心点，即：u1, u2, u3, ……, uk求偏导，然后求驻点，会如何呢？

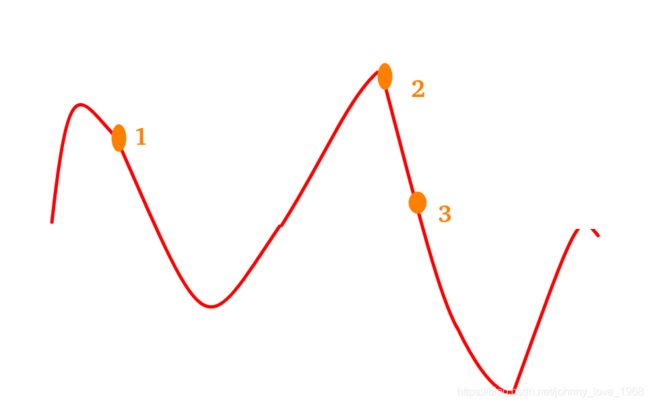
由此可见：有好多个极值点，从这个角度来说，k-means可以当作是那个所示函数在梯度下降上的一个应用。而依据上面这个数学推导，我们大致就可以画出目标函数的一个大致的图像：

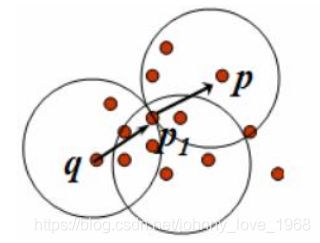
那么很显然，你到底初值选哪里，才更容易迭代到更好的结果，还真是不太容易搞，就像上图当中的，你选3点，肯定比1点能迭代到更小的损失值。说白了：初值选的好不好，直接影响到你能否迭代到一个好的结果。这就引申出了一个很重要的问题：k-means是初值敏感的。就像下面这个图：

如果我像左图那样选定初始点，那么久可能分成右侧那个图的样子。但是实际上，那个最大的圈，还可以至少分成两部分。

那么如何解决这个事情？

3. k-means ++

解决上述问题的一种思路是：初始选择的样本点，距离要尽可能的大。k-means算法一开始都会选初值。假定我选定了一个点，那么我把各个样本到这个点的距离全部计算一次，这样就得到了一组距离：d1, d2, d3 ……, dn。我们令D = d1 + d2 + …… + dn。然后得到若干个概率p1= d1/D, p2= d2/D, ……pn = dn/D。我们按照概率来选择哪个点是优先选择的点。

什么叫依概率选择呢？其实就是说，以上这若干的概率，哪个值最大，就越有可能会被选中，是不是一定选中呢？不一定！！不过，这个可能意味着运算量会很大。 有一段代码很好的说明了这个思路：

cluster_center = np.zeros((k,n)) #聚类中心
j= np.random.randint(m) #m个样本，在这m个样本当中随机选一个
cluster_center[0] = data[j][:] #随机选了一个中心j，那么给这个中心创建一个空列表，里面存储离这个中心合适的点
dis = np.zeros(m) - 1
i=0
while i<k-1:
    for j in ramge(m):
        d = (cluster_center[i]-data[j]) ** 2 #计算距离，这里这个距离是自己创造的一个标准
        d = np.sum(d)
        if (dis[j]<0) or (dis[j] > d): #离中心点距离要尽可能的大
            dis[j] = d
        j = random_select(dis) # 按照dis的加权来依概率选择样本
        i += 1
        cluster_center[i] = data[j][:]

如此一来，我们就得到了另一个算法：k-means++，相比纯粹的k-means，他就是多了一个这样的初始选择方式。这个方式颇有点这种味道：跳远比赛，不能每个人只跳一次，而是每个人跳好多次，综合考虑。

4.Mini-Batch K-Means

如果我们在k-means的基础上考虑SGD, BGD。如果我们所有点都考虑，那么就是SGD，但是如果我们从各个样本之间随机选若干个样本，然后做这些事情呢，那不就是BGD的思想。实际上，还真就有这种方式的k-means。这个方式有另外一个名字：Mini-Batch K-Means

5. k-means总结：

首先，我们看看它的优点:

• k-means是解决聚类问题的一种经典算法,简单、快速
• 对处理大数据集,该算法保持可伸缩性和高效率
• 当簇近似为高斯分布时,它的效果较好

但是，k-means的缺点也很明显，上面已经分析过了：

• 在簇的平均值可被定义的情况下才能使用,可能不适用于所有的应用场景
• 必须事先给出k(要生成的簇的数目，这个是个超参数，自己调整不是很好拿捏)，而且对初值敏感，对于不同的初始值可能会导致不同结果。
• 不适合于发现非凸形状的簇或者大小差别很大的簇
• 对躁声和孤立点数据敏感

与此同时，k-means可作为其他聚类方法的基础算法,如谱聚类

三.Canopy算法

这个算法，最开始其实是用来做空间索引的，但是它也可以应用于聚类问题。

这个算法的大体思路如下：

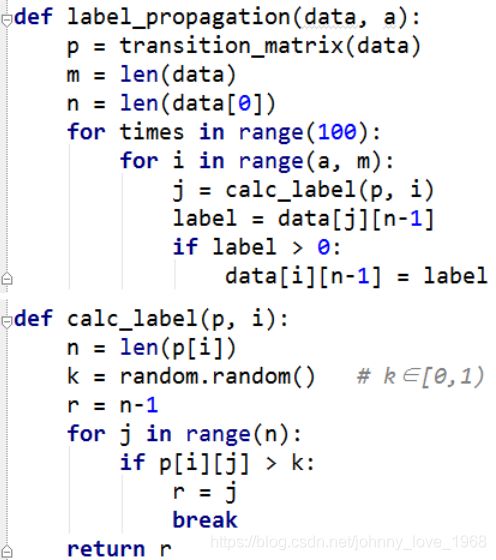
我们假定，有给定样本 x1 , x2 …… xm ，首先，我们给定先验值 r1 , r2 , 假设r1

• 我们让x1 , x2 ……xm 构成一个列表L; 然后，对每一个样本，都分别构造一个空列表，记为：c1, c2, ……, cm，如下图所示（画的不好，请见谅）：

• 我们随机选择L中的样本c,要求c的列表 Cc 为空:

• 计算L中样本 xj 与c的距离 dj

  • 若 dj < r1 ，则在L中删除 xj ,将 Cj 赋值为{c}
  • 否则，若 dj > r2 ，则将 Cj 增加{c}
  • 若L中没有不满足条件的样本c,算法结束。

怎么解释上面这个算法呢？

如果把Canopy当成聚类算法，那么r1,r2其实是两个半径。一个大一个小，假如：r1

因此，Canopy的一个关键就是：如何调整这两个圆的大小。这两个也是超参数，需要手动调，需要一定的经验积累。

四.聚类算法的评价指标

评价指标非常多。

1. 一些基本的

首先，先列出几个基本的：

• 均一性评价(Homogeneity)：一个簇只包含一个类别的样本,则满足均一性
  

• 完整性评价(Completeness)：同类别样本被归类到相同簇中,则满足完整性

  

• V-measure：均一性和完整性的加权平均

  [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3rj4hZDc-1620803235347)(/home/johnny/桌面/我的笔记/机器学习强化/聚类/15.png)]

2. ARI，AMI

ARI: Adjust Run Index。这个评价的思路，说直白点就是：随便挑两个样本，看他们是同一个类别的概率是多少。这个概率的值越大，说明分的并不成功（两个聚类，本应该属于两个类，结果却是一个，当然不成功了）

ARI本质上讲，就是评判两种聚类的相关性到底是多少，它的的思路是：

数据集S共有N个元素，其中，两个聚类结果分别是：X = {X1 , X2 , …… Xr }， Y = { Y1 , Y2 …… Ys}

X, Y这两个聚类各自所包含的元素是：a={ a1 , a2 , …… ar}， b = {b1 , b2 , …… bs}

我们记：
$$n_{ij}=|X_i\cap Y_i|$$

那么：

我们如果结合概率论当中的联合分部函数，其实就比较好理解了：

关于ARI公式：说明一下：

• 这些符号的含义是：index - （index的期望）, 最大的index，最小的index。
• 后面的C是概率里面的组合。后面那个是指：nij里面任意选两个（注意：不是平方)

对于AMI，它和ARI的区别很简单：ARI是算概率，AMI算的是互信息：

其中，MI代表的事互信息，相应的还有一个正则化互信息NMI：

而互信息期望E（MI）呢？

3. 轮廓系数(Silhouette)

计算样本i到同簇其他样本的平均距离di 。di越小，说明样本i越应该被聚类到该簇。将ai 称为样本i的簇内不相似度。簇C中所有样本的di均值称为簇C的簇不相似度。

当然，我们不能只计算一个样本的，得计算样本i到其他某簇Cj 的所有样本的平均距离bij ，这个bij称为样本i与簇C j 的不相似度。于是，我们得到了样本i与其他簇的不相似度列表，我们从中挑选最小值：
$$b_i=min(b_{i1},b_{i2},\dots \dots b_{ik})$$
b i 越大,说明样本i越不属于其他簇。

得到了簇内不相似度ai, 以及簇间不相似度bi之后，我们便得到了样本i的轮廓系数：
$$s(i)=\frac{b(i)-a(i)}{max\{a(i)-b(i)\}}=\{\begin{array}{l}1-\frac{a(i)}{b(i)},a(i)<b(i)\\ 0,a(i)=b(i)\\ \frac{b(i)}{a(i)}-1,a(i)>b(i)\end{array}$$
Note:

• 若s(i) 接近1,则说明样本i聚类合理；

  若s(i) 接近-1,则说明样本i更应该分类到另外的簇；

  若s(i) 近似为0,则说明样本i在两个簇的边界上。

• 所有样本的s(i)的均值称为聚类结果的轮廓系数。这个才是衡量聚类整体是否合理、有效的度量。

五.层次聚类

层次聚类方法对给定的数据集进行层次的分解,直到某种条件满足为止。

上面这么说可能有些抽象，但实际上层次聚类其实有很多场景。比如说学科，大的学科有文科，医学，哲学，理学，工学。但这些学科等等还可以往下划分，比如工学有建筑学，机械工程，计算机等等，以此类推，按照这个方式进行分裂的，就是Diana算法。也可以反着过来，即：把建筑，机械，计算机等凝聚成为工学，比如Agnes算法。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZXqtaIMn-1620911358214)(/home/johnny/桌面/我的笔记/机器学习强化/聚类/21.png)]

1. Agnes算法

Agnes算法是一种自底向上的策略,首先将每个对象作为一个簇,然后合并这些原子簇为越来越大的簇,直到某个终结条件被满足

该算法的思路是：

算法最初将每个对象作为一个簇，然后这些簇根据某些准则被一步步地合并。两个簇间的距离由这两个不同簇中距离最近的数据点对的相似度来确定。最终达到用户指定的簇数，或者达到某个阈值为止。

2.Diana算法

而Diana算法采用自顶向下的策略,它首先将所有对象臵于一个簇中,然后逐渐细分为越来越小的簇,直到达到了某个终结条件。是Agnes算法的反过程。

它的思路是：

首先将所有的对象初始化到一个簇中，然后根据某些准则将该簇分类。直到到达用户指定的簇数目或者两个簇之间的距离超过了某个阈值为止

3.簇间距离

我们注意到，在上面两个算法当中都提及了“某些准则”这个词，这个所谓的准则，就是你如何定义簇间距。关于粗间距，有这么几种方式：这当中的距离是什么，看“相似度衡量”这部分。

• 最小距离

  • 两个集合中最近的两个样本的距离
  • 容易形成链状结构（距离过小的化，就连在一块了）

• 最大距离

  • 两个集合中最远的两个样本的距离
  • 若存在异常值则不稳定

• 平均距离

  • 两个集合中样本间两两距离的平均值
  • 两个集合中样本间两两距离的平方和

这三种距离算法各有利弊，得根据现实情况来搞

六.密度聚类方法

1.简介

密度聚类算法的思路并不难：如果样本点的密度大于某阈值（用户指定），则将该样本添加到最近的簇中。

和之前介绍的聚类算法不同，这种算法受初值影响较小，因此，容错率较高，对噪声数据不敏感。但是，密度的计算往往运算量很大。因此在密度聚类算法当中，降维、建立空间索引的手段经常能用到。

常见的密度聚类算法有：DBSCAN，密度最大值算法等

2.密度的相关概念

这个密度，其实就是我们传统意义上理解的密度，但是在数学当中需要有一个量化的概念。这个概念首先是从邻域这个概念入手

ε-邻域：给定对象在半径ε内的区域（说白了，就是半径为ε的小圆）

有了邻域的概念，那么其他概念就容易理解了：

核心对象：对于给定的数目m，如果一个对象的ε-邻域至少包含m个对象,则称该对象为核心对象

直接密度可达：给定一个对象集合D，如果p是在q的ε-邻域内；而q是一个核心对象,我们说对象p从对象q出发是直接密度可达的。

密度可达：直观含义就是，如果直接密度可达具有传递性，p1->p2，密度可达，p2->p3密度可达，……p(n-1)->pn密度可达，最后，p1->pn也是密度可达的。如下图所示：

密度相连：如果对象集合D中存在一个对象o，使得对象p和q是从o关于ε和m密度可达的，那么对象p和q是关于ε和m密度相连的。这个概念和密度可达有很强的关联性，说直白点o是传递链中的某一环。如下图所示：

簇：关于簇的定义并不唯一，但是在密度聚类算法当中，它是这么定义的：最大的密度相连对象的集合。
噪声：不包含在任何簇中的对象称为噪声。

我们通过这些概念的定义，大体也能猜出来密度聚类算法的一些特点：

• 每个簇至少包含一个核心对象;
• 非核心对象可以是簇的一部分,构成了簇的边缘;
• 包含过少对象的簇被认为是噪声

3.DBSCAN算法

该算法的英文名：Density-Based Spatial（空间的） Clustering of Applications with Noise。从这个英文名当中，我们大致就可以猜出来它的特点，该算法能够把具有足够高密度的区域划分为簇，并且受噪声的影响较小。我们通过

DBSCAN算法的流程如下：

• 首先，选定一个点p，这个点的ε-邻域包含多于m个对象,则创建一个p作为核心对象的新簇;
• 寻找并合并核心对象直接密度可达的对象;
• 重复上述过程，当 没有新点可以更新簇时，算法结束。

通过第二点，似乎DBSCAN算法有点并查集的味道哈！！

4.密度最大值算法

在密度最大值算法当中，引入了另外一个概念：局部密度。这个局部密度的定义方式不止一种，大概有以下几种：

• 截断值：
  

这个式子本质上是数量的统计，在这个式子当中，dc 代表一个截断距离, ρi 即到对象i的距离小于dc 的对象的个数。由于该算法只对ρi 的相对值敏感, 所以对dc 的选择是稳健的,一种推荐做法是选择dc ，使得平均每个点的邻居数为所有点的1%-2%

• 高斯核函数相似度：
  

• K-近邻均值

与此同时，密度最大算法还引入了另外一个概念：高局部密度点距离

直白点解释：

• 高局部密度点：比我密度大的，却离我最近的那个点

• 高局部密度距离：比我密度大的，却离我最近的那个点的距离

不过，如果你遇到了一个密度最大的呢？显然，你就找不到比它密度更大的了，因此这个时候，高局部密度距离就做了一个修正：

在密度最大值方法中，关于簇，也有一个全新的定义，这当中出现了一个新的概念：簇中心

• 那些有着比较大的局部密度ρ i 和很大的高密距离 δ i 的点被认为是簇的中心;

  直白点解释：我所在的地方局部密度很大（说明我周围很拥挤），同时，密度比我还高的，离我很远，说明我所处的地方是一个簇，我就是这个簇的中心

• 高密距离 δi 较大但局部密度ρi较小的点是异常点;

  直白点解释：比我所在群落密度高的（为啥密度比我高？因为我周边就没有几个人），离我却很远，说明我太不合群了。所以我是异常点

在明确了什么是簇中心之后，根据簇中心之间的距离进行k-means，或者按照密度可达的方法，都可以进行分类

七.谱聚类

1.什么是谱

在谱聚类里面，大量运用了线性代数当中的特征值与特征向量的知识点。在了解谱之前，务必要了解这方面的内容，在了解了这方面内容之后，我们就可以引出谱的概念：方阵作为线性算子,它的所有特征值的全体统称方阵的谱。

这当中什么是线性算子呢？y = Ax， A是个矩阵。这样就相当于对x进行了一个线性变换。我们可以理解为y是通过某种映射得到的，即：y = map(x)，这个map其实就是这个A，就是线性算子。我们对A求特征值，把特征值拿出来所形成的东西就叫做谱

在知道了谱之后，我们就可以引申出谱半径的概念：其实就是最大的那个特征值。

2.算法简介

首先要说的是：谱聚类是一种基于图论的聚类方法，因此，我们必须对数据结构当中的图有所了解

我们先定义一个邻接矩阵：
$$w=(w_{ij}),i,j=1,2,\dots \dots ，n$$
邻接矩阵，学过数据结构的都知道这个其实表示的是结点之间的距离，在图中，每个结点和其他结点之间都有个距离，那么这个距离的和就是结点的度：
$$d_i=\sum _{j=1}^n{w}_{ij}$$
我们把这几个度组合在一起，形成一个对角矩阵D，就形成了度矩阵：

有了邻接矩阵，还有对角矩阵，我们就会得到拉普拉斯矩阵：L = W-D

我们可以求L的特征值(λ1,λ2,λ3,……λn)和特征向量(u1,u2,……，un)。所有特征向量都不止一个元素，可以组成一个特征向量矩阵，也是n*n的，如果我们想做k个类别的聚类（k

为什么这么做呢，为什么能够把特征向量当成特征选择的依据？我们举一个简单的例子解释一下：我们记一个元素全为1的列向量，假设为 Y则有D*Y - W*Y = 0 = 0*Y=>(D-W)*Y = 0*Y，因此Y一定是特征向量

我们假设n个样本当中，前r个是一个类，后n-r也是一个类，那么这两个类也有各自的拉普拉斯矩阵，因此也一定符合上面这个特征，即：全为1的列向量一定是特征向量，且对应特征值是1。(如图4.png那样子，注意后面那个矩阵是Yr, Yn-r （原本用的是1表示，但是写的像L，别误解了），但是等号后面那个是L，不是1)。这个式子表明一个事情：(Yr, Yn-r) 那个阵，起到了分类的作用。但是现实当中，(Yr, Yn-r)这个阵大概率没这么漂亮，即当中的1可能是0.9,0.95,0.8这种接近1的，而原本是0的，可能是0.1,0.05这种接近0的。毕竟机器学习分类总会出现误差

然后，我们看看这个特征向量矩阵，每一行都有k个数，那么第一行k个数就是第一个样本的特征，第二行的k个数就是第二个样本的特征。如此一来，我们就得到了n个样本的各自k个特征。万事俱备，我们运行一个k-means就可以了。

通过对样本数据的拉普拉斯矩阵的特征向量进行聚类,从而达到对样本数据聚类的目的

八.标签传递算法

这个基本了解一下就可以了。

在现实当中，我们得到一组样本。有的有标签，有的没有标签。于是，我们针对那些有标签的。他们都是给定的，我们就是针对这个标签来进行操作

标签传递算法(Label Propagation Algorithm, LPA)，将标记样本的标记通过一定的概率传递给未标记样本,直到最终收敛。

具体怎么传递呢？这个可以由用户定义