多目标优化
背景介绍
多目标优化在系统最优设计、最优控制以及社会科学等方面都具有广泛的应用,例如:坦克的变速箱不仅需要良好的传动精度,运动过程中还需要保持极高的稳定性;火箭的恒温层结构不仅需要极好的隔热性能,更需要保证良好的耐撞性能;航天飞行器外夹层结构在运行中面对不同工作环境需要实现不同的性能需求等。
多目标优化的特征为:一般情况下,多目标优化问题的各个子目标之间是相互矛盾的(一个子目标的改善可能会引起另几个子目标性能的降低),很难使得多个子目标同时达到最优值,只能在多个目标之间进行折中处理,使得各个子目标都尽可能达到最优解,从数学角度可以做如下描述:
min f 1 ( X ) , min f 2 ( X ) ⋯ min f n ( X ) X = { x 1 , x 2 ⋯ x n } T ∈ R n \min {f_1}(X),\min {f_2}(X) \cdots \min {f_n}(X) \qquad X = {\{ {x_1},{x_2} \cdots {x_n}\} ^T} \in {R^n} minf1(X),minf2(X)⋯minfn(X)X={x1,x2⋯xn}T∈Rn
该边界条件为:
g u ( X ) ≤ 0 , h v ( X ) = 0 u = 1 , 2 ⋯ p ; v = 1 , 2 ⋯ q {g_u}(X) \le 0,{h_v}(X) = 0 \qquad u = 1,2 \cdots p;v = 1,2 \cdots q gu(X)≤0,hv(X)=0u=1,2⋯p;v=1,2⋯q
多目标优化
多目标优化与单目标优化具有本质区别,主要体现于多目标优化问题的解并非唯一,而是存在一组由众多Pareto最优解组成的集合,具体如下图中蓝色曲线所示。
求解多目标优化问题最简单的方法是采用加权平均法,给每个目标函数分配相应的权重值,进而对所有目标函数加权后求和,数学上可以描述为:
min ∑ i = 1 n w i f i ( X ) X = { x 1 , x 2 ⋯ x n } T ∈ R n \min \sum\limits_{i = 1}^n {{w_i}{f_i}(X)} \qquad X = {\{ {x_1},{x_2} \cdots {x_n}\} ^T} \in {R^n} mini=1∑nwifi(X)X={x1,x2⋯xn}T∈Rn
该边界条件为:
g u ( X ) ≤ 0 , h v ( X ) = 0 u = 1 , 2 ⋯ p ; v = 1 , 2 ⋯ q {g_u}(X) \le 0,{h_v}(X) = 0 \qquad u = 1,2 \cdots p;v = 1,2 \cdots q gu(X)≤0,hv(X)=0u=1,2⋯p;v=1,2⋯q
其中,wi为对应目标函数的权重值,该种方法把多目标优化问题转换为单目标优化问题,简化了问题的难度,然而该方法具有相应的局限性,具体为:
-
权值难以确定;
-
各个目标之间量纲的不统一,可能会造成单目标优化问题鲁棒性差,采用优化算法过程中出现收敛性困难等问题;
-
多目标优化问题的帕累托解集包含更多有效信息。
加权求和法直观理解(两个优化目标):当给定权重后,相当于确定了曲线的斜率,进而从Pareto前沿上找到一点,使之到直线的距离最短。
程序代码
NSGA-Ⅱ是目前流行的多目标遗传算法之一,它降低了非劣排序遗传算法的复杂性,具有运行速度快,解集的收敛性好的优点,成为其他多目标优化算法性能的基准。网上下载、调试相应的程序代码,其中待优化的多目标优化问题数学模型为:
f 1 ( x ) = 1 − e − 4 x 1 sin 6 ( 6 π x 1 ) {f_1}(x) = 1 - {e^{ - 4{x_1}}}{\sin ^6}(6\pi {x_1}) f1(x)=1−e−4x1sin6(6πx1) f 2 ( x ) = ( 1 + 9 ( ∑ i = 1 6 x i 4 ) 0.25 ) ( 1 − ( f 1 ( x ) g ( x ) ) 2 ) {f_2}(x) = \left( {1 + 9{{\left( {\sum\limits_{i = 1}^6 {{{{x_i}} \over 4}} } \right)}^{0.25}}} \right)\left( {1 - {{\left( {{{{f_1}(x)} \over {g(x)}}} \right)}^2}} \right) f2(x)=⎝⎛1+9(i=1∑64xi)0.25⎠⎞(1−(g(x)f1(x))2)
其中:
0 ≤ x i ≤ 1 , i = 1 , 2 ⋯ 6 0 \le {x_i} \le 1, \qquad i = 1,2 \cdots 6 0≤xi≤1,i=1,2⋯6
具体程序代码如下:
chromosome = non_domination_sort_mod(chromosome,pro);
for i = 1 : gen
pool = round(pop/2);
tour = 2;
parent_chromosome = tournament_selection(chromosome,pool,tour);
mu = 20;
mum = 20;
offspring_chromosome = genetic_operator(parent_chromosome,pro,mu,mum);
[main_pop,temp] = size(chromosome);
[offspring_pop,temp] = size(offspring_chromosome);
intermediate_chromosome(1:main_pop,:) = chromosome;
intermediate_chromosome(main_pop + 1 : main_pop + offspring_pop,1 : M+V) = ...
offspring_chromosome;
intermediate_chromosome = ...
non_domination_sort_mod(intermediate_chromosome,pro);
chromosome = replace_chromosome(intermediate_chromosome,pro,pop);
if ~mod(i,10)
fprintf('%d\n',i);
end
end
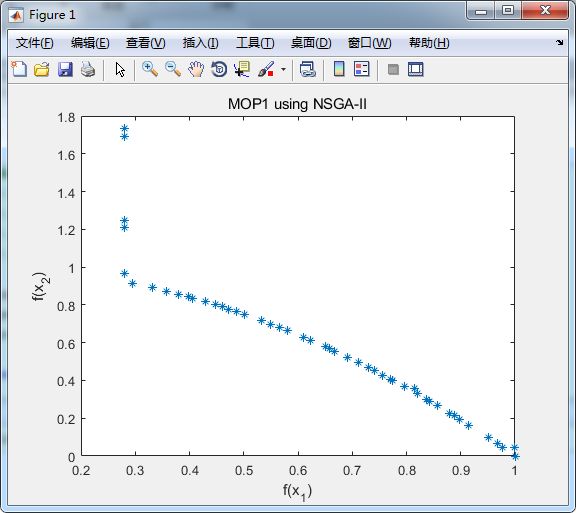
具体结果如下:
附:Pareto前沿的表述:在不使任何其他子目标受损的前提下,不可能再对该目标进行优化。