临界平面法简介

背景介绍

  临界平面法的基本思想是：裂纹的萌生具有一个危险平面，工程中可以将单元积分点的应力、应变值组装成一个综合参数，衡量不同截面裂纹萌生的难易程度，该方法广泛应用于工程构件在复杂应力状态下的疲劳寿命预测。

  调研发现，工程结构所选用的材料种类多种多样，其服役过程中承受的工作载荷也具有明显的差异，使得设备呈现不同的破坏模式，具体有：1. 应力作用下的疲劳裂纹萌生；2. 应变作用下的疲劳裂纹萌生；3. 应力和应变的共同作用使裂纹萌生等。因此，临界平面参数也具有多种表述方法，具体如图1所示：

图1 临界平面参数的表述方法

SWT 参数预测裂纹位置

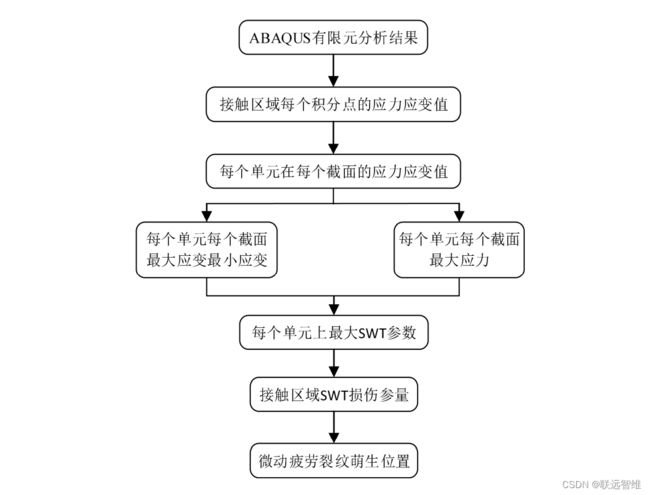
  研究表明，不管在低周疲劳还是高周疲劳，都可以用Smith-Watson-Topper（SWT）参量表征裂纹萌生位置以及寿命预测。SWT参数的求取过程如下所示：

• 1. 采用ABAQUS对有限元模型进行计算。求解疲劳载荷一个循环周期内接触区域所有单元每个积分点的应力和应变；
• 2. 采用Python提取ABAQUS的计算结果，把接触区域每个单元中每个积分点的应力应变输出到文件里边。研究表明，应力和应变采用积分点比节点更加准确；
• 3. 采用MATLAB，计算每个单元每个截面的应力应变值；

$${\sigma }_{11^{\prime }}=\frac{{\sigma }_{11}+{\sigma }_{22}}{2}+\frac{{\sigma }_{11}-{\sigma }_{22}}{2}\cos 2{\theta }_i+{\tau }_{12}\sin 2{\theta }_i$$
$${\epsilon }_{11^{\prime }}=\frac{{\epsilon }_{11}+{\epsilon }_{22}}{2}+\frac{{\epsilon }_{11}-{\epsilon }_{22}}{2}\cos 2{\theta }_i+{\epsilon }_{12}\sin 2{\theta }_i$$

• 4. 得到每个单元每个截面上的SWT参数，取最大值作为单元的SWT参数；
     $$SWT={\sigma }_{\max }{\sigma }_a$$
• 5. 得到接触区域SWT损伤参量的分布情况，确定裂纹萌生位置。

  SWT参量求取的具体流程图如图2所示：

图2 SWT参量求取流程图

程序代码

clear all;clc
danyuanchangdu=0.078125;
bianhao=1:104;
distance=danyuanchangdu.*(bianhao-105/2);
renyi=[1869, 1875, 1885, 1888,1893, 1896, 1913, 1916, 1943, 1946, 1947, 1950, 1955, 1958, 1967, 1970,2007,2010, 2011, 2014, 2019, 2022, 2031, 2034, 2103, 2106, 2107, 2110, 2115, 2118,2127, 2130, 2159, 2162, 2229, 2232, 2241, 2244, 2245, 2248, 2297, 2304, 2325,2328, 2329, 2332, 2362, 2363, 2370, 2371, 2382, 2383, 2470, 2471, 2474, 2475,2550, 2551, 2562, 2563, 2570, 2571, 2574, 2575, 2614, 2615, 2626, 2627, 2634,2635, 2638, 2639, 2694, 2695, 2706, 2707, 2714, 2715, 2718, 2719, 2800, 2801,2812, 2813, 2820, 2821, 2824, 2825, 2864, 2865, 2876, 2877, 2884, 2885, 2888,2889, 2944, 2945, 2956, 2957, 2964, 2965, 2968, 2969];（需要提取SWT单元的set集合）
set=renyi';
changdu=length(set);
node=zeros(changdu,1);
ynode=zeros(changdu,2);
for i=1:changdu
   node(i,1)=findelement(set(i,1));
   ynode(i,1)=findnode(node(i,1));
   ynode(i,2)=i;
end
setchange=zeros(changdu,3);
setchange(:,1)=sort(ynode(:,1),'descend');
for i=1:changdu
   setchange(i,2)=ynode(find(ynode(:,1)==setchange(i,1)),2);       
end
% swt=zeros(changdu,1);
for i=1:changdu
    vvv=swtqu(setchange(i,2)); 
    ylmax=max(vvv(1,:));
    ybfu=max(vvv(2,:))-min(vvv(2,:));
    setchange(i,3)=ylmax*ybfu;
end
jg(1,:)=distance;
jg(2,:)=setchange(:,3);
zuihoujieguo=jg';
plot(zuihoujieguo(:,1),zuihoujieguo(:,2))

function [ element4node ] =findelement( elementnumber )
element=[         ];（part单元集合）
element4node=element(find(element(:,1)==elementnumber),5);
end

function [ ynode ] = findnode( nodenumber )
node=[   ]（节点单元集合）
ynode=node(find(node(:,1)==nodenumber),3);
end

function [ yinglichu ] = swtqu( number )
S=[  ];
Le=[  ];
changdu=length(s(:,1));
yingli=zeros(changdu,37);
yingbian=zeros(changdu,37);
for j=1:changdu
    z=1;
 for i=0:5:180
        yingli(j,z)=0.5*(s(j,1)+s(j,2))+0.5*(s(j,1)-s(j,2))*cosd(2*i)+s(j,4)*sind(2*i);
        z=z+1;
 end 
end
yinglichu(1,:)=yingli(number,:);
for j=1:changdu
    z=1;
 for i=0:5:180
       yingbian(j,z)=0.5*(le(j,2)+le(j,3))+0.5*(le(j,2)-le(j,3))*cosd(2*i)+le(j,5)*sind(2*i);
        z=z+1;
 end 
end
yinglichu(2,:)=yingbian(number,:);
end