验证数据集和交叉验证以及偏差方差平衡
文章目录
- 一、验证数据集
-
- 1、验证数据集的引入
- 2、交叉验证 cross validation
- 3、交叉验证代码实例:
- 二、偏差方差平衡
-
- 1.什么是方差与偏差
- 2.模型有偏差和方差的原因
-
- 1、偏差:
- 2、方差:
- 3、算法的方差与偏差
- 3、方差与偏差的矛盾性
- 4、算法中的最大挑战是方差
一、验证数据集
1、验证数据集的引入
上篇结尾我们已经说过,对于只有训练数据集和测试数据集是不够的,因为对于模型来说,这两个数据集都是已知的,训练数据集用来训练模型,测试数据集用来调整超参数调整模型。但不论怎样,对于这个模型来说,没有一个未知数据的测试,会出现过拟合的现象。此时我们就需要一个验证数据集
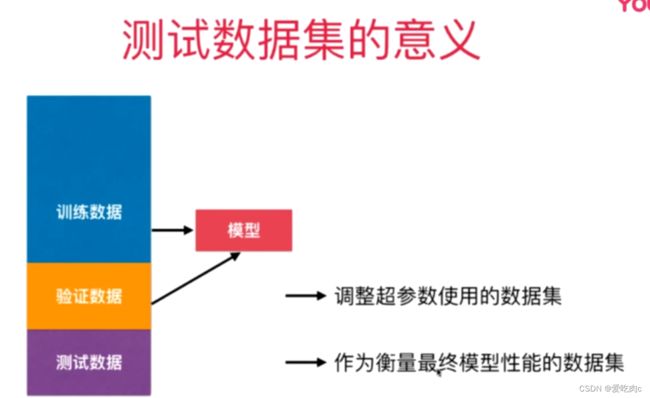
对于模型来说,训练数据集用来训练模型,验证数据集调整超参数,而测试数据集作为最终衡量模型性能的数据集。测试数据集对于模型来说是完全未知的。
2、交叉验证 cross validation
因为对于验证数据集它是随机的数据,可能会有极端值:
如果只使用一个验证数据集进行调参来获取模型的话,假设验证数据集中有极端的数据,就会导致该模型拟合验证数据集拟合的好,但是模型却不适用的情况。这种情况下,我们可以使用交叉验证的方式。
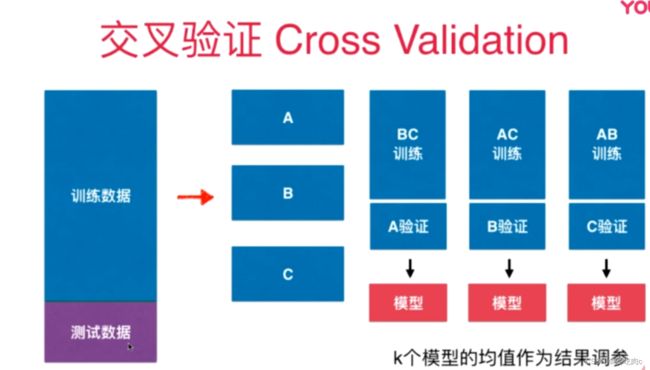
使用交叉验证的方式,会有多个验证数据集,我们使用交叉验证后的模型的均值作为评判模型的好坏(即使有一个极端情况也不影响)之后进行调参来调整模型。
3、交叉验证代码实例:
from sklearn import datasets
import numpy as np
digits=datasets.load_digits()
x=digits.data
y=digits.target
#这里先没有使用划分验证数据
测试train_test_split
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y)
from sklearn.neighbors import KNeighborsClassifier
#根据测试数据集来修改寻找最好的超参数
best_score,best_p,best_k=0,0,0
for k in range(1,11):
for p in range(1,6):
knn=KNeighborsClassifier(weights="distance",n_neighbors=k,p=p)
knn.fit(x_train,y_train)
score=knn.score(x_test,y_test)
if score>best_score:
best_score=score
best_p=p
best_k=k
print("best_score:",best_score)
print("best_p:",best_p)
print("best_k:",best_k)
交叉验证 有了验证数据集
knn=KNeighborsClassifier()
cross_val_score(knn,x_train,y_train) #默认k为3 交叉验证3次
from sklearn.model_selection import cross_val_score
best_score,best_p,best_k=0,0,0
for k in range(1,11):
for p in range(1,6):
knn=KNeighborsClassifier(weights="distance",n_neighbors=k,p=p)
scores=cross_val_score(knn,x_train,y_train)
score=np.mean(scores)
if score>best_score:
best_score=score
best_p=p
best_k=k
print("best_score:",best_score)
print("best_p:",best_p)
print("best_k:",best_k)

可以看到 与不区分验证数据的结果不同
通过使用验证数据来调整参数获得的模型来测试数据
best_knn=KNeighborsClassifier(weights="distance",n_neighbors=1,p=3)
best_knn.fit(x_train,y_train)
best_knn.score(x_test,y_test)
我们可以看到,虽然该结果比不使用验证数据的结果值低,但是使用交叉验证的获得的模型应该更值得信赖
回顾网格搜索,其实网格搜索使用的也是交叉验证
from sklearn.model_selection import GridSearchCV
para_grid=[
{'weights':['distance'],
'n_neighbors':[i for i in range(1,11)],
'p':[i for i in range(1,6)]}]
grid_search=GridSearchCV(knn,para_grid)
grid_search.fit(x_train,y_train)
grid_search.best_params_
二、偏差方差平衡
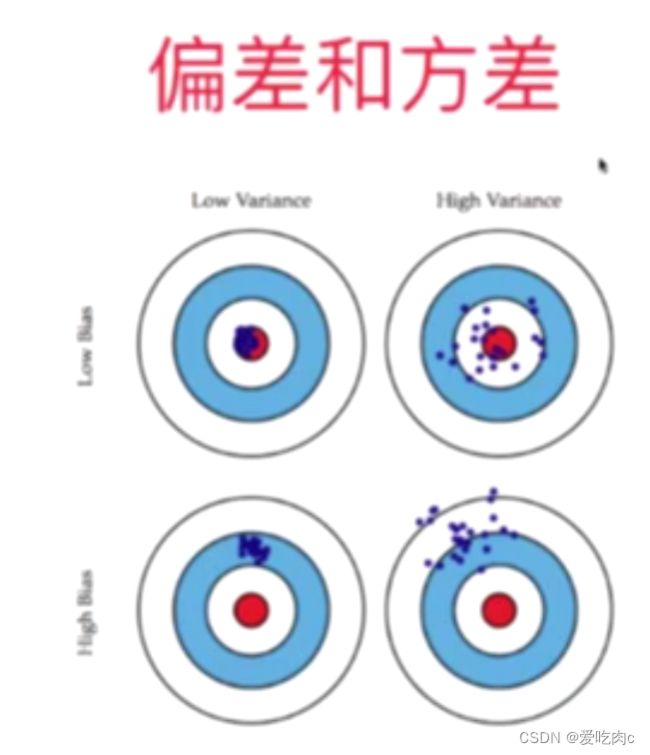
1.什么是方差与偏差
2.模型有偏差和方差的原因
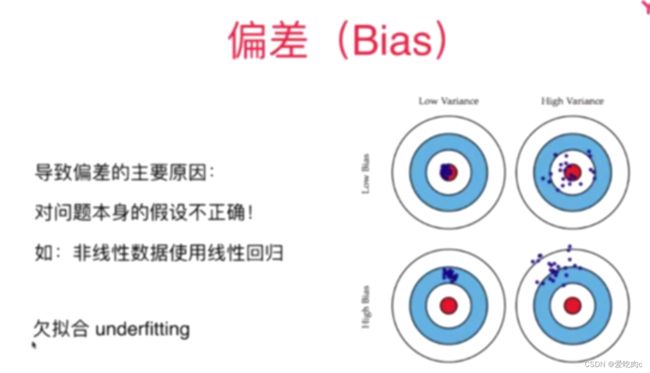
1、偏差:
简单来说,就是我们对数据本身的认识不够充分不够合理
2、方差:
如过拟合,对测试数据拟合的很好,但是由于模型太过复杂,泛化能力弱,导致其他数据的拟合程度不好,方差过大