(六)多项式回归
文章目录
- 前言
- 1. 一个例子
- 2. 多项式回归模型
- 3. 代码实现
前言
这篇文章介绍多项式回归。
1. 一个例子
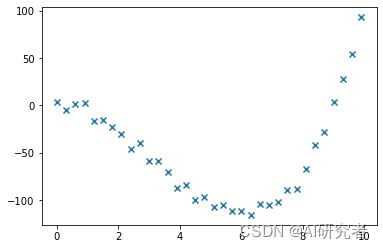
线性回归可以很好地拟合线性分布的数据,但是对于非线性的数据却派不上用场,例如下面的数据:
这是一个简单的例子,它只有一个特征,输出变量 y y y 仅仅是关于这一个特征 x x x 的函数,但是线性回归却无法拟合它。之前学习了一种局部加权线性回归算法,它自然可以很好地拟合这样的数据分布,但是那种算法要求对每一种预测都要重新训练参数,它的拟合效果的确非常好,但是有一个很大的缺点就是时间代价太大。
观察这样的数据分布,发现线性函数无法拟合它,那么非线性函数呢?例如二次函数能否拟合它?如果二次函数拟合效果不好,那么三次函数能不能较好地拟合它?二次函数是一种对称的函数,上述图形并不对称,因此二次函数的拟合效果也未必好,不过可以从数据分布中看出,二次函数的拟合应该是要比一次函数(线性函数)好的。次数上升后,拟合效果会好一些,那么三次函数呢?熟悉三次函数的人可能会看出,只要三次函数的四个系数选取恰当,那么这个三次函数就比较接近数据分布。根据泰勒公式我们可以知道,如果一个函数 n n n 阶连续可导,那么我们可以用 n n n 阶多项式来逼近这个函数。这也给了我们启发,使用多项式来拟合非线性的数据分布!
2. 多项式回归模型
如果想对输出变量 y y y 和特征向量 x = ( x 0 , x 1 , ⋯ , x n ) = ( 1 , x 1 , ⋯ , x n ) x=(x_0,x_1,\cdots,x_n)=(1,x_1,\cdots,x_n) x=(x0,x1,⋯,xn)=(1,x1,⋯,xn) 作回归,根据上面的启发,我们想用一个多项式函数来预测 y y y ,假设我们使用 2 阶多项式来预测 y y y ,也就是说我们想寻找参数 θ \theta θ 使:
y = θ 0 + ∑ i = 1 n θ i x i + ∑ i ⩽ j θ i j x i x j y=\theta _0+\sum_{i=1}^n{\theta _ix_i}+\sum_{i\leqslant j}{\theta _{ij}x_ix_j} y=θ0+i=1∑nθixi+i⩽j∑θijxixj
我们只有特征 x 1 , x 2 , ⋯ , x n x_1,x_2,\cdots ,x_n x1,x2,⋯,xn ,要想获得特征的平方呢,怎么做呢?很简单!只需要把训练集中每个特征取 2 2 2 次方就可以了。获得 x i x j x_ix_j xixj 的方法也就是将 x i x_i xi 列和 x j x_j xj 列相乘。也就是说,我们有 m m m 个训练样本,矩阵 X X X 为:
X = ( 1 x 1 ( 1 ) ⋯ x n ( 1 ) 1 x 1 ( 2 ) ⋯ x n ( 2 ) ⋮ ⋮ ⋱ ⋮ 1 x 1 ( m ) ⋯ x n ( m ) ) X=\left( \begin{matrix} 1& x_{1}^{\left( 1 \right)}& \cdots& x_{n}^{\left( 1 \right)}\\ 1& x_{1}^{\left( 2 \right)}& \cdots& x_{n}^{\left( 2 \right)}\\ \vdots& \vdots& \ddots& \vdots\\ 1& x_{1}^{\left( m \right)}& \cdots& x_{n}^{\left( m \right)}\\ \end{matrix} \right) X=⎝⎜⎜⎜⎜⎛11⋮1x1(1)x1(2)⋮x1(m)⋯⋯⋱⋯xn(1)xn(2)⋮xn(m)⎠⎟⎟⎟⎟⎞
我们只需要把矩阵 X X X 的除了第 1 1 1 列之外的所有列取平方后和所有列两两相乘后形成的新列加入到这个矩阵中即可,这样就会形成一个新的矩阵 X n e w X_{new} Xnew ,然后用这个矩阵当作原来的矩阵,使用普通的线性回归训练参数就可以了,使用正规方程解法就是:
θ = ( X n e w T X n e w ) − 1 X n e w T y \theta =\left( X_{new}^{T}X_{new} \right) ^{-1}X_{new}^{T}y θ=(XnewTXnew)−1XnewTy
同样也可以使用梯度下降等解法,和普通的线性回归一模一样。这就是多项式回归。
上面介绍了二阶多项式回归的方法,更高阶的多项式回归同理。如果数据使用比较低阶的多项式就可以较好的拟合,那么多项式回归便是一个较好的方法,但是如果低阶多项式不能很好地拟合数据,需要次数较高的多项式来拟合,那么这时会导致新构造的矩阵特征维度太大,这将不利于训练。
3. 代码实现
代码中分别使用了一次函数(普通的线性回归)、二次函数和三次函数来拟合上述实例:
import numpy as np
import matplotlib.pyplot as plt
# 创造数据
def CreateData():
X = np.arange(0,10,0.3)
y = np.empty(X.shape[0])
for i in range(X.shape[0]):
y[i] = 1.1*X[i]**3 - 10*X[i]**2 + X[i] + np.random.uniform(-10,10)
return X[:,np.newaxis], y
X, y = CreateData()
X = np.insert(X, 0, 1, axis = 1)
# 数据可视化
plt.scatter(X[:,1], y, marker = 'x')
# 使用普通线性回归预测(一次函数)
theta = np.dot(np.linalg.inv(np.dot(X.T, X)), np.dot(X.T, y))
# 可视化回归曲线
t = np.linspace(-1, 11, 100)
plt.plot(t, theta[0] + theta[1] * t, c = 'blue')
# 使用二次函数回归
col_new = X[:,1]**2 # 新增加一列
X = np.hstack([X, col_new[:,np.newaxis]])
theta = np.dot(np.linalg.inv(np.dot(X.T, X)), np.dot(X.T, y))
# 可视化回归曲线
t = np.linspace(-1, 11, 100)
plt.plot(t, theta[0] + theta[1] * t + theta[2] * t**2, c = 'yellow')
# 使用三次函数回归
col_new = X[:,1]**3 # 新增加一列
X = np.hstack([X, col_new[:,np.newaxis]])
theta = np.dot(np.linalg.inv(np.dot(X.T, X)), np.dot(X.T, y))
# 可视化回归曲线
t = np.linspace(-1, 11, 100)
plt.plot(t, theta[0] + theta[1] * t + theta[2] * t**2 + theta[3] * t**3, c = 'red')
# 加标注
plt.legend([r"$y=\theta_0+\theta_1x$",
r"$y=\theta_0+\theta_1x+\theta_2x^2$",
r"$y=\theta_0+\theta_1x+\theta_2x^2+\theta_3x^3$"])
plt.show()
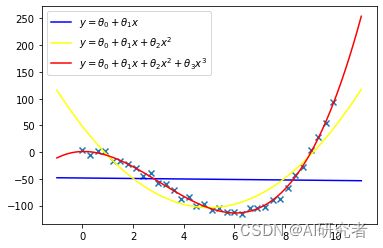
拟合结果如下:
显然,可以看出,一次函数根本没用,二次函数拟合较一次函数来说效果好些,但是也可以明显感到欠拟合,三次函数的拟合效果明显较好。这里没有使用更高阶多项式拟合,由于高阶多项式的逼近能力会变高,因此对于高阶多项式,就要考虑到过拟合的问题,选择合适的阶数在使用该算法时很重要。