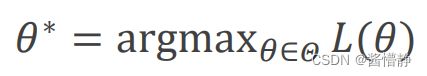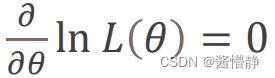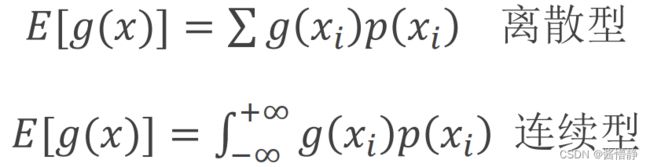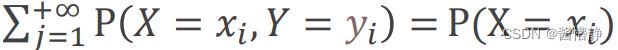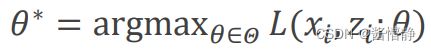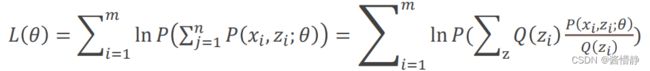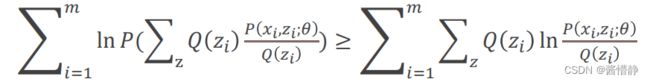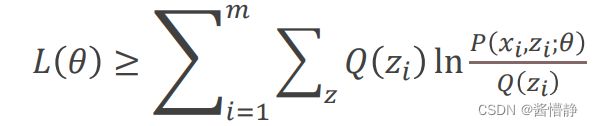【机器学习】EM算法

EM算法

---

一、似然函数与极大似然估计

例一
现有一个不透明的罐子，里面装有质地、大小均相同而颜色不同的黑白两种球（数目未知）。现要求在经过有限次抽样后（放回式），求解罐中黑白球的比例。
假设当前对该罐子进行了100次放回式抽样，其中有70次抽出白球，30次抽出黑球，问该罐中黑白球的比例最可能是多少？
答案很明显，黑：白 = 3：7。

例二
一个林子内只有小明和猎人在打猎（已知小明的命中率为30%，猎人的命中率为80%），当你看到一只鸟被击落时，你认为最有可能是谁打中的？
答案肯定是猎人。

但我想问的是，你做出这样推理的背后，是依赖于什么理论？

在前面两个例子中，我们都基于一些已知数据，对某个先验事件做出了推断。例一中，若没有告诉你抽样的具体情况，我们将难以对罐中黑白球的比例做出推测；例二中，若不知道小明和猎人的命中率，我们的答案将是“一半一半”。但是，当有了某次实验的数据后，我们在对该事件的先验概率做出推测时，就会往倾向于该实验数据的方向靠近，即体现为“原始分布最可能的取值”，这实际上就是极大似然估法的灵魂所在。
比如例一中，既然抽出白球的次数更多，那么就自然地认为罐子中白球的比例更大；例二中，既然猎人的命中率更高，那么就自然地认为击中鸟的人更可能是猎人而非小明。

一般的，若设总体的概率函数为 (; ) , ∈ , 其中 是一个未知参数（或一组未知参数构成的参数向量） ， 是可能取值的参数空间，(₁, ₂,…, ) 是来自该总体的样本。于是可以得到样本的联合概率密度为：

称 ()为样本的似然函数。
由于似然函数() 是以参数 为变量的函数，因此似然函数的目的就是在样本(₁, ₂,…, ) 固定的前提下，以寻找最优的 来使似然函数最大，即：

接下来为了求出 ∗ ，就是要求使得似然函数 () 最大的 。这是求解自变量的问题而与函数值无关，因此为了
便于计算，我们通常令 () 为 ln () ,然后再对 ln () 求偏导，并在偏导取值为 0 处得到最终的 ∗（实际上就是求极值的步骤） ：

---

二、Jenson不等式

设 是定义域为实数的函数，如果对于所有的实数 ，′′() ≥ 0，则称 是凸函数。Jenson不等式定义为：对于任意凸函数 ,都有函数值的期望大于等于期望的函数值。即：

(()) ≥ (())

若 是严格的凸函数，当且仅当 P (X=()) = 1（即X是常量时），上式等号成立。
当Jenson不等式应用于凹函数时，不等号方向相反。

---

三、数学期望的相关定理

若随机变量 的分布用分布列 () （或密度函数 () ）来表示，则 的某一函数 () 的数学期望为：

例，离散型分布列：

X	1	2	3
P	1/5	3/5	1/5

则：
() = 1 × (1/5) + 2 × (3/5) + 3 × (1/5) = 2
(()) = 1² × (1/5) + 2² × (3/5) + 3² × (1/5) = 4.4 , () = ²

---

四、边缘分布列

在二位离散随机变量 (X, Y) 的联合分布列 { P( = , = ) } 中，对 求和所得分布列：

称为 X 的分布列。
类似地，对 求和所得分布列：

称为 Y 的分布列。

---

五、坐标上升法

---

六、EM算法

1. 概论

在讲 EM 算法前，必须请大家记住其使用场景：
给出了观测变量的数据，但是这些数据依赖于一些隐藏变量（且该隐藏变量的值也是未知的），问出现如此观测数据的概率是多少？

例子
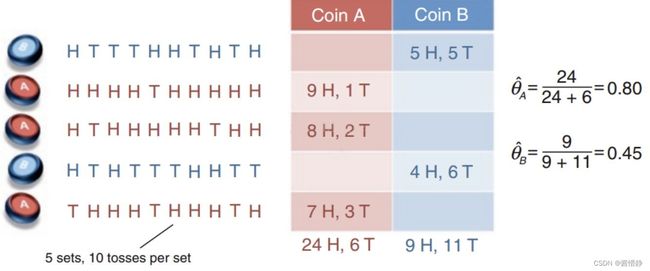
现在有两个硬币 A 和 B ，这两个硬币都是有偏的（设参数 、 分别为硬币A、B正面朝上的概率）。现在做5组实验，每次实验从两个硬币中随机抽一个，然后连续抛10次。下图所示为五组实验数据。如果我们知道了每次抛的是哪个硬币，那么计算上面那两个参数就非常的简单。

但如果不知道每次抛的是哪个硬币呢？如下图所示：

总结来看，就是已知两枚硬币抛掷后的分布，但不知道具体是哪个抛出来的（“使用哪个硬币”就是隐变量），而“使用哪个硬币”这个信息又对抛掷后的结果有影响。即，隐变量和我们想要求的参数互相纠缠，形成了一个死循环，而求解该问题就需要用到 EM 算法了。
从这个角度看，EM算法与极大似然估法十分相似：已知观测随机变量的数据，问出现这样的观测随机变量的数据的概率是多少？不同的是，EM算法还考虑了隐变量的影响，并试图对其进行求解。

实际上，EM算法正是基于极大似然估法。前面曾说道，极大似然估法的目标是：

现在，我们的模型不变，且目标均是对某个事件（此处是抛硬币）已出现的观测结果进行推测——怎样的原分布最可能出现这样的结果？但不同的是，现在我们还多了一个未知参数（隐变量），因此现在要求的目标是：

此时，目标函数为：

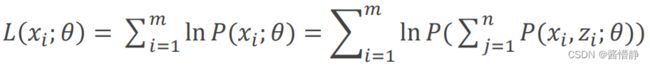
为什么该步骤成立？考虑两个变量 , ，则上式实际上正是计算边缘分布列的逆过程。
在上式中， 和 均未知。因此在求解时，传统的求导方法不再适用。只能通过固定其中一个值来求解另一个，然后不断重复这个过程，直到该过程收敛（坐标上升法）。但这里有个问题：为什么该过程收敛？这个问题将放在最后进行解答。

2. 算法流程

EM算法的思路如下：

1. 给 、 一个初始值；
2. 分别计算每组实验在抛掷硬币A、硬币B的情况下所得概率，并根据该概率值去分别计算两硬币正面朝上次数的期望值。因此，此步骤也被称为“E过程”；
3. 分别用第 2 步中计算的每组期望值来计算 _A⁽⁾、_B⁽⁾；
4. 将计算得到的 _A⁽⁾、_B⁽⁾ 回代第 2、3 步，并不断迭代得到 _A⁽⁺¹⁾、_B⁽⁺¹⁾ , 直至收敛（或到一定精度）。此步骤的本质就是不断修正两硬币正面朝上次数的期望值，即期望最大化，因此也被称为“M过程”；

注：第 2 步中为什么要计算期望进行迭代而不直接以各自的概率值进行迭代？这个问题将在后面进行解答。

下面用一个例子来帮助理解（EM算法的流程详解）：

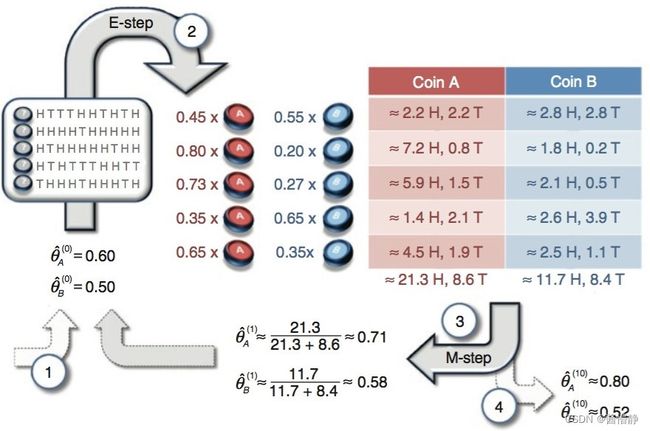
1. 给 、 赋始值： _A⁽⁰⁾ = 0.6 、 _B⁽⁰⁾ = 0.5，表示硬币A、B正面朝上的概率分别为0.6、0.5；
2. “E过程”（仅以第一组实验为例）：
   ① 计算概率。第一组实验结果是5正5反，则硬币A、B抛出该事件的概率分别为 = 0.6⁵ × 0.4⁵, = 0.5⁵ × 0.5⁵。于是可以得到，“第一组实验选择的硬币是A”的概率为 _A / (_A+_B) = 0.449 ≈ 0.45，则“第一组实验选择硬币是B”的概率为1 − 0.45 = 0.55 ；
   ② 计算期望。若选择的是硬币A，则正、反面朝上次数的期望值分别为 0.45 × 5H ≈ 2.2, 0.45 × 5 ≈ 2.2，若选择的是硬币B，则正、反面朝上次数的期望值分别为 0.55 × 5H ≈ 2.8, 0.55 × 5 ≈ 2.8 ；
   ③ 重复①和②，直到计算完该组实验中的所有数据。
3. 更新 、 。利用第 2 步求得的期望值重新计算 _A⁽¹⁾ = 21.3 / (2.13+8.6) ≈ 0.71 、 _B⁽¹⁾= 11.7 / (11.7+8.4) = 0.58 （从该结果可以看出，经过一次迭代， _A 、_B 的值已经往真实值的方向逼近了一点）；
4. “M过程”。将参数再带回2、3中求解，不断迭代直至收敛。

3. 算法的推导

首先来看待优化的目标函数：

我们要估计参数就是要极大化这个对数似然函数，然而隐变量 和参数 均未知，因此我们的解决方法就是假设（初始化参数）。首先假设一个模型参数 ⁽⁰⁾ ，然后可以计算出隐变量的概率分布 () ，根据 (, ) = ( | )()（条件概率公式），再将 () 带入上述公式可以得到一个关于模型参数 的函数，再对该函数进行极大化就可以得到一个新的 。有了这个新的 再对每个样本重新计算其隐变量的分布，迭代至收敛，这就是EM算法的基本思想。换言之，直接对原函数进行最大化是不现实的，因为计算相当复杂，故引入Jenson不等式简化。
对上面的对数似然函数引入隐变量 的某个分布函数 () ，则：

由于函数() = ln()是一个凹函数，因此根据Jenson不等式可知：

即：

也就是说我们找到了 () 的一个下界。但是，需要注意的是，该不等式右侧中的 实际上是 , 即某一次迭代时暂定的假设值（当然，随着迭代次数的增多，该值会越来越趋近于真实值）。
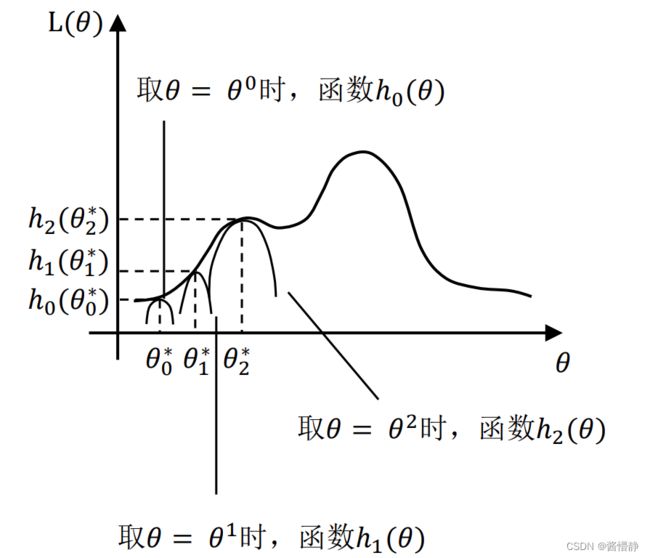
下图中，最开始初始化 = ⁰（ ⁰ 可任意取值），然后根据它可求似然函数一个紧的下界曲线，也就是图中的 ℎ₀() ，该函数上的值虽然都小于似然函数的值，但至少有一点 ₀* 可以满足等号（所以称为紧下界），即最大化函数 ℎ₀() 我们就可以得到至少与似然函数刚好相等的位置（设该处为 ₀），对应的横坐标 ₀ 就是我们的新的 ，（下一轮迭代时被设为 ¹ ）。如此进行，只要保证随着 的更新，每次最大化的新曲线都比上次的更大，那么算法收敛，最后就能最大化到似然函数的极大值处。

思考：EM算法一定能求到全局最优解么？
答：当优化的目标函数是凸函数时，一定能求到全局最优解；如果不是，则只能取到局部最优解。

4. 敛散性证明

END

---