反向传播——机器学习

目录

一、实验内容

二、实验过程

1、算法思想

2、算法原理

3、算法分析

三、源程序代码

四、运行结果及分析

 五、实验总结

---

 

一、实验内容

---

1. 掌握线性反向传播的原理；
2. 掌握线性反向传播的算法Python实现；
3. 熟悉非线性反向传播的原理；
4. 掌握非线性反向传播的算法Python实现。

二、实验过程

---

1、算法思想

---

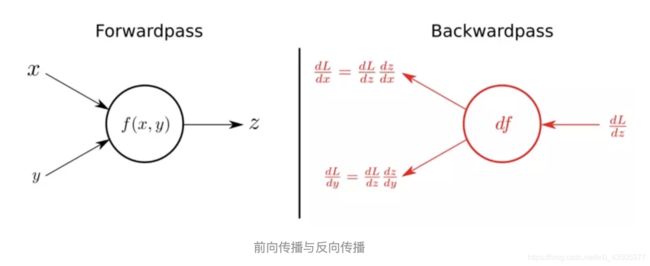
        反向传播是利用函数的链式求导来进行推导的，目的是通过不断调整权重和偏置来不断减小误差，最终得到误差最小的神经网络。

2、算法原理

---

        反向传播线性回归的思想是一样的，是一种与最优化方法（如梯度下降法）结合使用的，逐渐调节参数，用来训练人工神经网络的常见方法。

3、算法分析

---

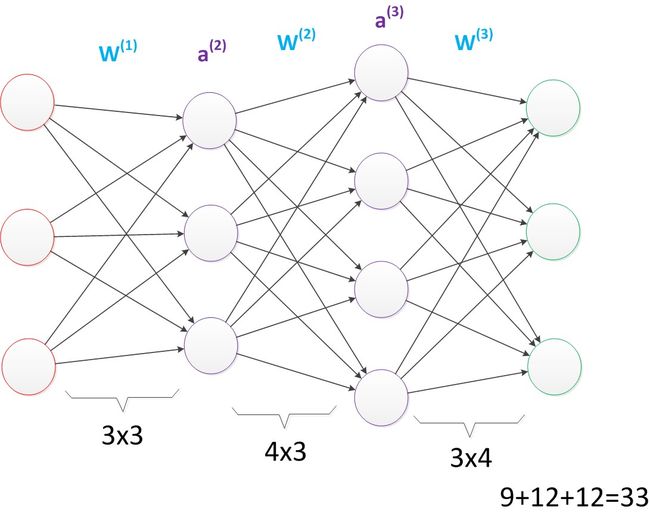
（1）将训练集数据输入到n的输入层，经过隐藏层，最后达到输出层并输出结果，这是n的前向传播过程；

（2）由于n的输出结果与实际结果有误差，则计算估计值与实际值之间的误差，并将该误差从输出层向隐藏层反向传播，直至传播到输入层；

（3）在反向传播的过程中，根据误差调整各种参数的值；不断迭代上述过程，直至收敛。

三、源程序代码

---

import numpy as np
import math
import tensorflow as tf
import matplotlib.pyplot as plt
 
 
def grad_sigmoid(n):
    # 求sigmoid梯度
    return np.array(tf.sigmoid(1.0 - tf.sigmoid(n)))
 
 
def g(p):
    # 目标函数值
    t = []
    index = 0
    for i in p:
        t.append(1.0 + math.sin(p[index] * np.pi/4))
        index += 1
    return t
 
 
# 采用1-2-1网络，输入为1维，隐藏层为2维，输出为一维
# 隐藏层为对数-S型层
# 输出层为线性层
# N为batch size; 训练集一批401个，输入p在[-2,2]区间以0.01间距的等距采样，有对应的目标向量t=g(p)。
# D_in 输入维度
# H为隐藏层维度
# D_out 输出维度
N, D_in, H, D_out = 401, 1, 2, 1
 
# 生成训练集，输入向量p和目标向量t
p = np.linspace(start=-2.0, stop=2.0, num=N)
t = g(p)
p = np.array([p])
t = np.array([t])
print("输入向量：")
print(p)
print("输入向量长度：")
print(len(p))
print("目标向量：")
print(t)
print("目标向量长度：")
print(len(t))
 
print("随机生成初始权值矩阵：")
# w1 = np.random.randn(H, D_in)
# w2 = np.random.randn(D_out, H)
w1 = np.array([[-0.27], [-0.41]])
w2 = np.array([[0.09, -0.17]])
print("W1：")
print(w1)
print("W2：")
print(w2)
 
print("随机生成初始偏置")
# b1 = np.random.randn(H, D_in)
# b2 = np.random.randn(D_out, D_out)
b1 = np.array([[-0.48], [-0.13]])
b2 = 0.48
print("b1：")
print(b1)
print("b2：")
print(b2)
 
# 设置学习率为0.1
alpha = 0.01
 
for i in range(900):
    # 前向传播计算
    n1 = w1.dot(p) + b1
    a1 = np.array(tf.sigmoid(n1))
    a2 = w2.dot(a1) + b2
    # n2==a2  输出层为线性层
    # 计算误差
    loss = np.square(a2 - t).sum()/N
    if i % 10 == 0 or i == 900:
        print(i, loss)
 
    # 最后层敏感度计算，最后一层为线性函数，导数为1，
    s2 = -2.0 * (t - a2)
    # w2_sub 为 w2的对角矩阵
    w2_sub = np.array([[w2[0][0], 0], [0, w2[0][1]]])
    s1 = (grad_sigmoid(n1).T.dot(w2_sub) * s2.T).T
    grad_w2 = np.array(np.zeros((D_out, H)))
    grad_w1 = np.array(np.zeros((H, D_in)))
    grad_b2 = np.array(np.zeros((D_out, D_out)))
    grad_b1 = np.array(np.zeros((H, D_in)))
    # 计算批处理的梯度
    for m in range(0, N - 1):
        grad_w2 += 1 / N * a1.T[m] * s2[0][m]
        grad_w1 += 1 / N * np.array([p[0][m] * s1.T[m]]).transpose()
        grad_b2 += 1 / N * s2[0][m]
        grad_b1 += 1 / N * np.array([s1.T[m]]).transpose()
    # 更新权重偏置，向梯度相反的方向下降
    w1 -= alpha * grad_w1
    w2 -= alpha * grad_w2
    b1 -= alpha * grad_b1
    b2 -= alpha * grad_b2
print("训练结束:")
print("w1:")
print(w1)
print("w2:")
print(w2)
print("b1:")
print(b1)
print("b2:")
print(b2)
# test = np.array([np.random.uniform(-2, 2, size=N)])
test = np.array([np.linspace(start=-2.0, stop=2.0, num=N)])
out = w2.dot(tf.sigmoid(w1.dot(test) + b1)) + b2
plt.xlabel('in')
plt.ylabel('out')
plt.xlim(xmax=2, xmin=-2)
plt.ylim(ymax=2, ymin=0)
colors1 = '#00CED1'
colors2 = '#054E9F'
area1 = np.pi * 2 ** 1  # 点面积
area2 = np.pi * 1 ** 1  # 点面积
# 画散点图
plt.scatter(p, t, s=area1, c=colors1, alpha=1, label='origin')
plt.scatter(test, out, s=area2, c=colors2, alpha=0.5, label='test')
plt.legend()
plt.show()

四、运行结果及分析

---

 五、实验总结

---

        反向传播就是要将神经网络的输出误差，一级又一级地传播到神经网络的输入。在该过程中，需要计算每一个权重对总的损失函数的影响， 即损失函数对每个权重的偏导。根据权重对误差的影响，再乘以步长，就可以更新整个神经网络的权重。 当一次反向传播完成之后，网络的参数模型就可以得到更新。

        更新一轮之后,接着输入下一个样本， 算出误差后又可以更新一轮，再输入一个样本，又来更新一轮，通过不断地输入新的样本迭代地更新模型参数，就可以缩小计算值与真实值之间的误差，最终完成神经网络的训练。