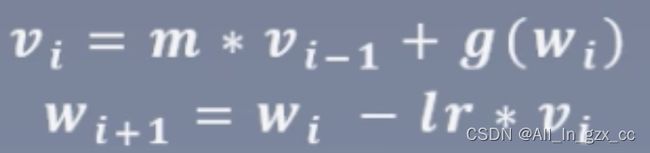pytorch快速上手（8）-----pytorch优化器简介

深度学习五个步骤： 数据 ——> 模型 ——> 损失函数 ——> 优化器 ——> 迭代训练，通过前向传播，得到模型的输出和真实标签之间的差异，也就是 损失函数，有了损失函数之后，模型反向传播得到 参数的梯度，接下来就是 优化器根据这个梯度去更新参数。

一、简介

pytorch的优化器：更新模型参数。

在更新参数时一般使用梯度下降的方式去更新。梯度下降常见的基本概念

• 导数：函数在指定坐标轴上的变化率；
• 方向导数：指定方向上的变化率；
• 梯度：一个向量，方向为方向导数取得最大值的方向。

所以梯度是一个向量，方向是导数取得最大值的方向，也就是增长最快的方向，而梯度下降是沿着梯度的负方向去变化。

二、optimizer

class Optimizer:
    defaults: dict
    state: dict
    param_groups: List[dict]
 
    def __init__(self, params: _params_t, default: dict) -> None: ...
    def __setstate__(self, state: dict) -> None: ...
    def state_dict(self) -> dict: ...
    def load_state_dict(self, state_dict: dict) -> None: ...
    def zero_grad(self, set_to_none: Optional[bool]=...) -> None: ...
    def step(self, closure: Optional[Callable[[], float]]=...) -> Optional[float]: ...
    def add_param_group(self, param_group: dict) -> None: ...

属性

• defaults: 优化器的超参数，主要存储一些学习率、momentum的值等等
• state: 用来存储参数的一些缓存。例如使用momentum的时候，需要用到前几次的梯度，就存在这。
• params_groups: 管理参数组。是一个list。list的每一个元素是一个字典。字典中有一个’params’的key，其对应的值才是真正的参数。

方法

1. zero_grad()

清空所管理参数的梯度。

参数是一个张量，张量有梯度grad.

pytorch有一个特性：张量梯度是不会清零的。在每一次反向传播采用autograd计算梯度的时候，是累加的。

所以应当在梯度求导之前（backward之前）把梯度清零。

2. step()

step()会执行当前采用的优化器策略进行参数更新，具体的策略有很多种，例如随机梯度下降法，momentum加动量的方法，自适应学习率的方法等，后面会具体介绍。

3. add_param_group()

添加一组参数到优化器中。

优化器可以管理很多参数，这些参数是可以分组的。我们对不同组的参数可以有不同的超参数的设置。例如在模型的fintune中，对模型前面特征提取的部分希望他的学习率小一些，更新的慢一些；而后面的自己定义的全连接层，希望学习率更大一些。这样就可以把整个模型分成两组，一组是前面特征提取的参数，一组是后面全连接层的参数

4. state_dict()

获取优化器当前状态信息字典。

optimizer = optim.SGD([weight], lr=0.1, momentum=0.9)
opt_state_dict = optimizer.state_dict()
 
print("state_dict before step:\n", opt_state_dict)
 
for i in range(10):
    optimizer.step()
 
print("state_dict after step:\n", optimizer.state_dict())
# 训练10次之后将模型的参数保存下来
torch.save(optimizer.state_dict(), os.path.join(BASE_DIR, "optimizer_state_dict.pkl"))

5. load_state_dict()

加载状态信息字典

optimizer = optim.SGD([weight], lr=0.1, momentum=0.9)
state_dict = torch.load(os.path.join(BASE_DIR, "optimizer_state_dict.pkl"))
 
print("state_dict before load state:\n", optimizer.state_dict())
optimizer.load_state_dict(state_dict)
print("state_dict after load state:\n", optimizer.state_dict())

学习率

在梯度下降的过程中，学习率起到控制参数更新的一个步伐的作用。

若没有学习率，随着迭代次数的增多，loss值反而越来越大，说明在参数更新过程中，步子迈的太大，反而跳过了最优值，这时需要一个参数来控制这个跨度，这个就是学习率。

动量

Momentum(动量、冲量)：结合当前的梯度与上一次更新的信息，用于当前更新。

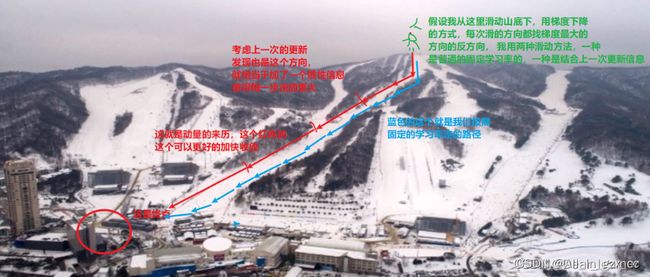
所以在考虑动量的情况下，可以更快的走到山脚下，也就是说参数更新的更快。那动量是怎么用于参数更新的呢？

先看一下指数加权平均的概念，指数加权平均在时间序列中经常用于求取平均值的一个方法，它的思想是这样，求取当前时刻的平均值，距离当前时刻越近的那些参数值，它的参考性越大，所占的权重就越大，这个权重是随时间间隔的增大呈指数下降，所以叫做指数滑动平均。公式如下：

v_t是当前时刻的一个平均值，这个平均值有两项构成，

• 一项是当前时刻的参数值 θ_t , 所占的权重是1-β， 这个 β 是个参数。
• 另一项是上一时刻的一个平均值，权重是 β 。

假设给了一系列 day-温度 的数据，求解第100天温度的平均值


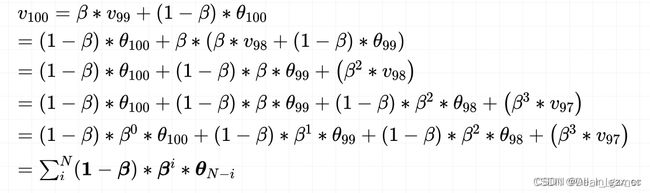
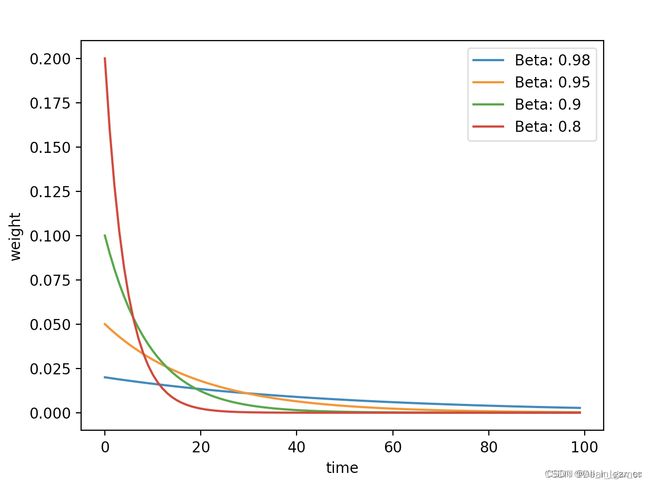
可以发现，beta 越小，就会发现它关注前面一段时刻的距离就越短，比如0.8， 会发现往前关注20天基本上后面的权重都是0了，意思就是说这时候是平均的过去20天的温度， 而0.98关注过去的天数会非常长，也就是说这时候平均的过去50天的温度。所以β 在这里控制着记忆周期的长短，或者平均过去多少天的数据对现在的影响。参数β 常设置为0.9，也就是 1/(1-β) 等于10，关注过去10天左右的温度，如下图是不同β 下温度的一个变化曲线：

• 红色的那条，是 beta=0.9， 也就是过去10天温度的平均值；
• 绿色的那条，是 beta=0.98， 也就是过去50天温度的平均值；
• 黄色的那条，beta=0.5， 也就是过去2天的温度的平均。

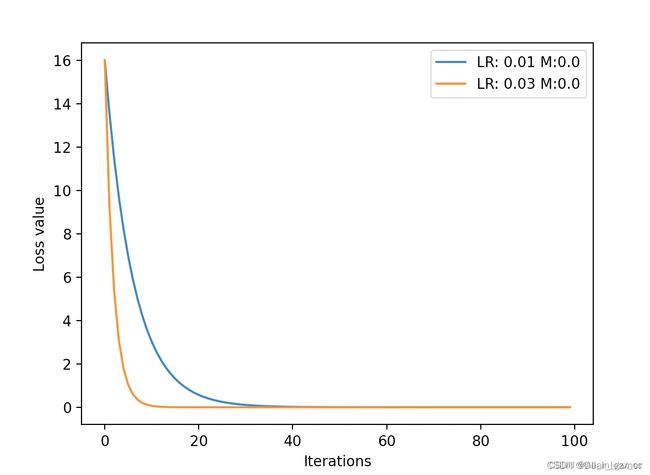
在理解指数加权平均之后，来看一下加了Momentum的梯度下降，其基本思想是计算梯度的指数加权平均，并利用该梯度更新权重，pytorch中实现：

• 普通的梯度下降：
  
• Momentum梯度下降：
  
  所以当前梯度的更新量会考虑到当前梯度， 上一时刻的梯度，前一时刻的梯度，这样一直往前，越往后的权重越小。下面通过代码来了解一下momentum的作用

def func(x):
    return torch.pow(2*x, 2)    # y = (2x)^2 = 4*x^2        dy/dx = 8x

iteration = 100
m = 0.0     # .9 .63

lr_list = [0.01, 0.03]

momentum_list = list()
loss_rec = [[] for l in range(len(lr_list))]
iter_rec = list()

for i, lr in enumerate(lr_list):
    x = torch.tensor([2.], requires_grad=True)

    momentum = 0. if lr == 0.03 else m
    momentum_list.append(momentum)

    optimizer = optim.SGD([x], lr=lr, momentum=momentum)

    for iter in range(iteration):

        y = func(x)
        y.backward()

        optimizer.step()
        optimizer.zero_grad()

        loss_rec[i].append(y.item())

for i, loss_r in enumerate(loss_rec):
    plt.plot(range(len(loss_r)), loss_r, label="LR: {} M:{}".format(lr_list[i], momentum_list[i]))
plt.legend()
plt.xlabel('Iterations')
plt.ylabel('Loss value')
plt.show()

三、常见优化器介绍

pytorch中的优化器可以大体分为两类：

• 一类是基于SGD及其优化，
• 另一类是Per-parameter adaptive learning rate methods（逐参数自适应学习率方法），如AdaGrad、RMSProp、Adam等。

1. BGD（Batch Gradient Descent）

梯度更新规则：
BGD采用整个训练集的数据来计算 cost function 对参数的梯度

缺点：
由于在一次更新中，是对整个数据集计算梯度，所以训练速度慢，如果训练集很大，需要消耗大量的内存，且全量梯度下降不能进行在线模型参数更新。

2. Stochastic Gradient Descent（SGD）

SGD是通过每个样本迭代更新一次，如果样本量很大的情况，那么可能只用到其中的部分样本数据参数就能更新到最优，对比BGD,一次迭代需要全部的数据，一次迭代不可能达到最优，迭代10次就需要将训练集训练10次。

缺点：
1、如果样本中噪音比较多，使得SGD并不是每次迭代向着整体最优化的方向进行；
2、SGD因为更新比较频繁，会造成 cost function 有严重的震荡；
3、可能会收敛到局部最优，但由于震荡会跳过最优。

3. Mini-Batch Gradient Descent(MBGD)

梯度更新规则：
MBGD 每次利用一小批样本，即n个样本进行计算，这样可以降低参数更新时的方差，收敛更稳定，另一方面可以利用矩阵操作来进行更有效的梯度计算。

缺点：
1、MBGD 不能保证很好的收敛性，learning rate 如果选择太小，收敛速度慢，选择太大，会使得 cost function 在极小值附近震荡（一种解决措施是先设置大一点的learning rate，当达到某个阈值时，就减少learning rate，不过这个阈值要提前设定）；
2、对所有的参数更新时应用同样的learning rate，如果数据是稀疏的，更希望对频率出现低的特征进行大一点的更新。

注：深度学习中的SGD优化算法是指mini-batch SGD(MBGD)

torch.optim.SGD(params, lr=<required parameter>, momentum=0, dampening=0, weight_decay=0, nesterov=False)

• param: 管理的参数组
• lr: 初识学习率
• momentum：动量系数，
• beta weight_decay: L2正则化系数
• nesterov: 是否采用NAG

4. SGD + Momentum（动量梯度下降）

将之前的梯度都联系起来，不再是每一次梯度都是独立的情况。让每一次参数的更新方向不仅仅取决于当前位置的梯度，还受到上一次参数更新方向的影响。

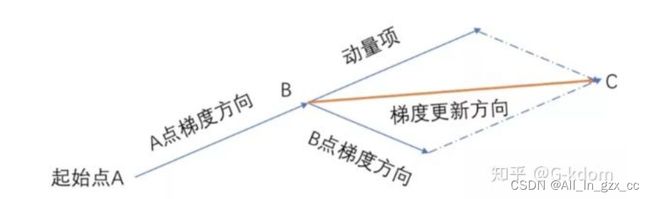
优点：
通过过去梯度信息来优化下降速度，如果当前梯度与之前梯度方向一致时候，收敛速度得到加强，反之则减弱。换句话说，加快收敛同时减小震荡。

缺点：
可能在下坡过程中累计动量太大，冲过极小值点。

另外，pytorch中的 SGD with momentum 已经在optim.SGD中的参数momentum中实现。

5. Nesterov accelerated gradient（NAG）

NAG（加速梯度下降）相比于动量梯度下降的区别是，通过使用未来梯度来更新动量。即将下一次的预测梯度∇θJ(θ−η⋅m)考虑进来。
参数更新公式为：

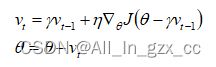
与普通的momentum的区别如下图

在pytorch中，通过参数nesterov=True 来实现Nesterov Momentum。
优点：
1、相对于动量梯度下降法，因为NAG考虑到了未来预测梯度，收敛速度更快（如上图）。
2、当更新幅度很大时，NAG可以抑制震荡。例如起始点在最优点的左侧←，γm对应的值在最优点的右侧→，对于动量梯度而言，叠加η∇1 使得迭代后的点更加远离最优点→→。而NAG首先跳到γm对应的值→，计算梯度为正，再叠加反方向的η∇2 ←，从而达到抑制震荡的目的。

6. Adagrad（自适应梯度/Adaptive Gradient）

AdaGrad在训练过程中动态调整学习率，对不同参数根据累计梯度平方和更新不同学习率。
参数更新公式：

其中⊙是点乘，相当于求梯度的平方。ϵ为防止除0及维持数据稳定的极小项，一般取10^(-6)
因为s是梯度平方和的累加项，所以：

1、梯度一直变化较大的参数，学习率下降也较快，即高频特征使用较小学习率。
2、梯度一直变化较小的参数，学习率下降也较慢，即低频特征使用较大学习率。
3、因为累加性，学习率的趋势是不断衰减的，这也符合迭代后期靠近极值点时需设置较小的学习率的直观想法。

优点： 每个变量都有适应自己的学习率

缺点： 由于学习率的不断衰减在迭代过程早期衰减过快可能直接导致后期收敛动力不足，使得AdaGrad无法获得满意的结果。

pytroch实现：

torch.optim.Adagrad(params, lr=0.01, lr_decay=0, weight_decay=0, initial_accumulator_value=0)

7. RMSProp（Root Mean Square Propagation）

针对于AdaGrad的学习率衰减过快缺点，RMSProp通过指数加权移动平均(累计局部梯度信息)替代累计平方梯度和来优化AdaGrad，使得远离当前点的梯度贡献小。
迭代更新公式：

其中β为RMSProp的衰减因子。s为关于梯度的指数加权移动平方和，初始值为0。⊙为点乘，即对应项乘积。

优点： 在Adagrad基础上添加衰减因子，在学习率更新过程中权衡过去与当前的梯度信息，减轻了因梯度不断累计导致学习率大幅降低的影响，防止学习过早结束。

缺点： 引入了超参数β,增加模型复杂性。同时依赖全局学习率η。
pytorch中的实现：

torch.optim.RMSprop(params, lr=0.01, alpha=0.99, eps=1e-08, weight_decay=0, momentum=0, centered=False)

8. AdaDelta（自适应增量）

AdaDelta是针对于Adagrad的另一种优化，它相对于RMSProp，使用参数θ变化量的指数加权移动平方和替换了全局学习率η。其思想是利用一阶方法近似模拟二阶牛顿法。

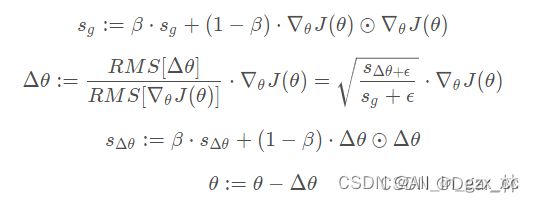
sg为关于梯度的指数加权移动平方和，sΔθ是关于参数θ变化量的指数加权移动平方和。二者初始值设为0。ϵ是维持数据稳定的常数，一般设置为10^{-6}。
在AdaDelta优化中，分子可以看成一个动量加速项，通过指数加权方式累积先前的梯度变化量。分母项则是与RMSProp一样，所以也可以将RMSProp看成是AdaDelta的一种特殊情况。
优点：
不需要人工设置学习率。

9. Adam（自适应矩阵/Adaptive Momentum Estimation）

Adam融合了RMSProp及Momentum的思想，做到了学习率自适应和动量加速收敛的效果。
参数更新公式为：

其中第三和第四项是s和m的偏差修正值，使得过去的梯度权值和为1，防止值过小。超参数一般设置为β=0.999, γ=0.9, ε=10^-8​。

torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0, amsgrad=False)

参考链接： https://blog.csdn.net/Dear_learner/article/details/123219459