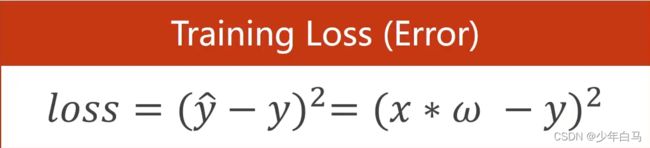【PyTorch】深度学习实战之线性模型
本文主要是参考B站刘二大人的视频讲解
本文的主要内容是PyTorch深度学习实践的线性模型。类似于初中的求函数:先给出几个点,让你求出函数,然后再给一个x坐标,让你求出y坐标,或者是类似于高中的最小二乘法,但是在深度学习领域我们需要去找损失函数为0的w值,而不是人眼或者手动算出来
import numpy as np
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
def forward(x):
return x * w
def loss(x, y):
y_pred = forward(x)
return (y_pred - y) * (y_pred - y)
w_list = []
mse_list = []
for w in np.arange(0.0, 4.1, 0.1): # 0-4,每隔0.1取一个点
print('w=', w)
l_sum = 0
for x_val, y_val in zip(x_data, y_data):
y_pred_val = forward(x_val)
loss_val = loss(x_val, y_val)
l_sum += loss_val
print('\t', x_val, y_val, y_pred_val, loss_val)
print('MSE=', l_sum / 3)
print('\n')
w_list.append(w)
mse_list.append(l_sum / 3)
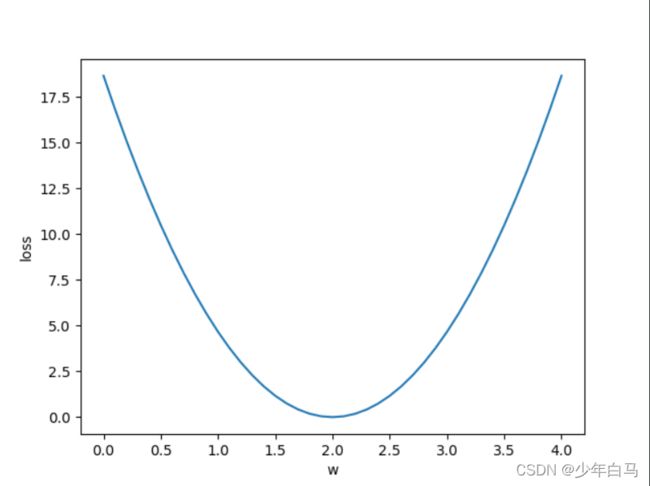
plt.plot(w_list, mse_list)
plt.xlabel('w')
plt.ylabel('loss')
plt.show()
输出结果:
w= 0.0
1.0 2.0 0.0 4.0
2.0 4.0 0.0 16.0
3.0 6.0 0.0 36.0
MSE= 18.666666666666668
w= 0.1
1.0 2.0 0.1 3.61
2.0 4.0 0.2 14.44
3.0 6.0 0.30000000000000004 32.49
MSE= 16.846666666666668
w= 0.2
1.0 2.0 0.2 3.24
2.0 4.0 0.4 12.96
3.0 6.0 0.6000000000000001 29.160000000000004
MSE= 15.120000000000003
w= 0.30000000000000004
1.0 2.0 0.30000000000000004 2.8899999999999997
2.0 4.0 0.6000000000000001 11.559999999999999
3.0 6.0 0.9000000000000001 26.009999999999998
MSE= 13.486666666666665
w= 0.4
1.0 2.0 0.4 2.5600000000000005
2.0 4.0 0.8 10.240000000000002
3.0 6.0 1.2000000000000002 23.04
MSE= 11.946666666666667
w= 0.5
1.0 2.0 0.5 2.25
2.0 4.0 1.0 9.0
3.0 6.0 1.5 20.25
MSE= 10.5
w= 0.6000000000000001
1.0 2.0 0.6000000000000001 1.9599999999999997
2.0 4.0 1.2000000000000002 7.839999999999999
3.0 6.0 1.8000000000000003 17.639999999999993
MSE= 9.146666666666663
w= 0.7000000000000001
1.0 2.0 0.7000000000000001 1.6899999999999995
2.0 4.0 1.4000000000000001 6.759999999999998
3.0 6.0 2.1 15.209999999999999
MSE= 7.886666666666666
w= 0.8
1.0 2.0 0.8 1.44
2.0 4.0 1.6 5.76
3.0 6.0 2.4000000000000004 12.959999999999997
MSE= 6.719999999999999
w= 0.9
1.0 2.0 0.9 1.2100000000000002
2.0 4.0 1.8 4.840000000000001
3.0 6.0 2.7 10.889999999999999
MSE= 5.646666666666666
w= 1.0
1.0 2.0 1.0 1.0
2.0 4.0 2.0 4.0
3.0 6.0 3.0 9.0
MSE= 4.666666666666667
w= 1.1
1.0 2.0 1.1 0.8099999999999998
2.0 4.0 2.2 3.2399999999999993
3.0 6.0 3.3000000000000003 7.289999999999998
MSE= 3.779999999999999
w= 1.2000000000000002
1.0 2.0 1.2000000000000002 0.6399999999999997
2.0 4.0 2.4000000000000004 2.5599999999999987
3.0 6.0 3.6000000000000005 5.759999999999997
MSE= 2.986666666666665
w= 1.3
1.0 2.0 1.3 0.48999999999999994
2.0 4.0 2.6 1.9599999999999997
3.0 6.0 3.9000000000000004 4.409999999999998
MSE= 2.2866666666666657
w= 1.4000000000000001
1.0 2.0 1.4000000000000001 0.3599999999999998
2.0 4.0 2.8000000000000003 1.4399999999999993
3.0 6.0 4.2 3.2399999999999993
MSE= 1.6799999999999995
w= 1.5
1.0 2.0 1.5 0.25
2.0 4.0 3.0 1.0
3.0 6.0 4.5 2.25
MSE= 1.1666666666666667
w= 1.6
1.0 2.0 1.6 0.15999999999999992
2.0 4.0 3.2 0.6399999999999997
3.0 6.0 4.800000000000001 1.4399999999999984
MSE= 0.746666666666666
w= 1.7000000000000002
1.0 2.0 1.7000000000000002 0.0899999999999999
2.0 4.0 3.4000000000000004 0.3599999999999996
3.0 6.0 5.1000000000000005 0.809999999999999
MSE= 0.4199999999999995
w= 1.8
1.0 2.0 1.8 0.03999999999999998
2.0 4.0 3.6 0.15999999999999992
3.0 6.0 5.4 0.3599999999999996
MSE= 0.1866666666666665
w= 1.9000000000000001
1.0 2.0 1.9000000000000001 0.009999999999999974
2.0 4.0 3.8000000000000003 0.0399999999999999
3.0 6.0 5.7 0.0899999999999999
MSE= 0.046666666666666586
w= 2.0
1.0 2.0 2.0 0.0
2.0 4.0 4.0 0.0
3.0 6.0 6.0 0.0
MSE= 0.0
w= 2.1
1.0 2.0 2.1 0.010000000000000018
2.0 4.0 4.2 0.04000000000000007
3.0 6.0 6.300000000000001 0.09000000000000043
MSE= 0.046666666666666835
w= 2.2
1.0 2.0 2.2 0.04000000000000007
2.0 4.0 4.4 0.16000000000000028
3.0 6.0 6.6000000000000005 0.36000000000000065
MSE= 0.18666666666666698
w= 2.3000000000000003
1.0 2.0 2.3000000000000003 0.09000000000000016
2.0 4.0 4.6000000000000005 0.36000000000000065
3.0 6.0 6.9 0.8100000000000006
MSE= 0.42000000000000054
w= 2.4000000000000004
1.0 2.0 2.4000000000000004 0.16000000000000028
2.0 4.0 4.800000000000001 0.6400000000000011
3.0 6.0 7.200000000000001 1.4400000000000026
MSE= 0.7466666666666679
w= 2.5
1.0 2.0 2.5 0.25
2.0 4.0 5.0 1.0
3.0 6.0 7.5 2.25
MSE= 1.1666666666666667
w= 2.6
1.0 2.0 2.6 0.3600000000000001
2.0 4.0 5.2 1.4400000000000004
3.0 6.0 7.800000000000001 3.2400000000000024
MSE= 1.6800000000000008
w= 2.7
1.0 2.0 2.7 0.49000000000000027
2.0 4.0 5.4 1.960000000000001
3.0 6.0 8.100000000000001 4.410000000000006
MSE= 2.2866666666666693
w= 2.8000000000000003
1.0 2.0 2.8000000000000003 0.6400000000000005
2.0 4.0 5.6000000000000005 2.560000000000002
3.0 6.0 8.4 5.760000000000002
MSE= 2.986666666666668
w= 2.9000000000000004
1.0 2.0 2.9000000000000004 0.8100000000000006
2.0 4.0 5.800000000000001 3.2400000000000024
3.0 6.0 8.700000000000001 7.290000000000005
MSE= 3.780000000000003
w= 3.0
1.0 2.0 3.0 1.0
2.0 4.0 6.0 4.0
3.0 6.0 9.0 9.0
MSE= 4.666666666666667
w= 3.1
1.0 2.0 3.1 1.2100000000000002
2.0 4.0 6.2 4.840000000000001
3.0 6.0 9.3 10.890000000000004
MSE= 5.646666666666668
w= 3.2
1.0 2.0 3.2 1.4400000000000004
2.0 4.0 6.4 5.760000000000002
3.0 6.0 9.600000000000001 12.96000000000001
MSE= 6.720000000000003
w= 3.3000000000000003
1.0 2.0 3.3000000000000003 1.6900000000000006
2.0 4.0 6.6000000000000005 6.7600000000000025
3.0 6.0 9.9 15.210000000000003
MSE= 7.886666666666668
w= 3.4000000000000004
1.0 2.0 3.4000000000000004 1.960000000000001
2.0 4.0 6.800000000000001 7.840000000000004
3.0 6.0 10.200000000000001 17.640000000000008
MSE= 9.14666666666667
w= 3.5
1.0 2.0 3.5 2.25
2.0 4.0 7.0 9.0
3.0 6.0 10.5 20.25
MSE= 10.5
w= 3.6
1.0 2.0 3.6 2.5600000000000005
2.0 4.0 7.2 10.240000000000002
3.0 6.0 10.8 23.040000000000006
MSE= 11.94666666666667
w= 3.7
1.0 2.0 3.7 2.8900000000000006
2.0 4.0 7.4 11.560000000000002
3.0 6.0 11.100000000000001 26.010000000000016
MSE= 13.486666666666673
w= 3.8000000000000003
1.0 2.0 3.8000000000000003 3.240000000000001
2.0 4.0 7.6000000000000005 12.960000000000004
3.0 6.0 11.4 29.160000000000004
MSE= 15.120000000000005
w= 3.9000000000000004
1.0 2.0 3.9000000000000004 3.610000000000001
2.0 4.0 7.800000000000001 14.440000000000005
3.0 6.0 11.700000000000001 32.49000000000001
MSE= 16.84666666666667
w= 4.0
1.0 2.0 4.0 4.0
2.0 4.0 8.0 16.0
3.0 6.0 12.0 36.0
MSE= 18.666666666666668
课后作业
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
x_data = [1.0, 2.0, 3.0]
y_data = [1.5, 4.0, 6.5]
W, B = np.arange(0.0, 4.1, 0.1), np.arange(-2.0, 2.1, 0.1) # 规定W,B的区间
w, b = np.meshgrid(W, B, indexing='ij') # 构建矩阵坐标
def forward(x):
return x * w + b
def loss(y_pred, y):
return (y_pred - y) * (y_pred - y)
mse_list = []
l_sum = 0
for x_val, y_val in zip(x_data, y_data):
y_pred_val = forward(x_val)
loss_val = loss(y_pred_val, y_val)
l_sum += loss_val
mse_list.append(l_sum / 3)
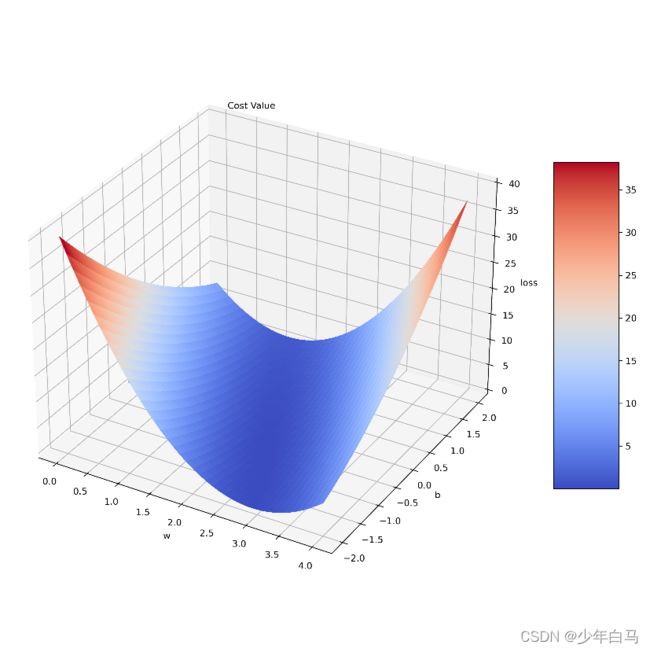
fig = plt.figure(figsize=(10, 10), dpi=300)
# 将figure变为3d
ax = Axes3D(fig)
# 绘图,rstride:行之间的跨度 cstride:列之间的跨度
surf = ax.plot_surface(w, b, np.array(mse_list[0]), rstride=1, cstride=1, cmap=cm.coolwarm, linewidth=0,
antialiased=False)
ax.set_zlim(0, 40)
# 设置坐标轴标签
ax.set_xlabel("w")
ax.set_ylabel("b")
ax.set_zlabel("loss")
ax.text(0.2, 2, 43, "Cost Value", color="black")
fig.colorbar(surf, shrink=0.5, aspect=5)
plt.show()
| 如果努力了,却还是没有出现效果,说明你正在为你以前的懒惰赎罪,只要坚持下去拼个头破血流,这段时间过后你就会发现,你爬到了一个不可想象的高度 |
|---|