【Python】Python中的经典时间序列预测模型总结
时间序列预测是机器学习中一个经常被忽视的重要领域。时间序列在观察之间添加了显式的顺序依赖性:时间维度。这个额外的维度既是一个约束,也是一个提供额外信息来源的结构。
时间序列
时间序列分析
使用经典统计时,主要关注的是时间序列的分析。
时间序列分析涉及开发能够最好地捕捉或描述观察到的时间序列的模型,以了解根本原因。该研究领域寻求时间序列数据集背后的“为什么”。
时间序列预测
在时间序列数据的经典统计处理中,对未来进行预测称为外推。更现代的领域关注该主题并将其称为时间序列预测。预测涉及采用适合历史数据的模型并使用它们来预测未来的观察结果。
描述性模型可以借用未来(即平滑或去除噪声),它们只寻求最好地描述数据。预测的一个重要区别是未来是完全不可用的,只能根据已经发生的事情来估计。
时间序列的组成部分
时间序列分析提供了一系列技术来更好地理解数据集。也许其中最有用的是将时间序列分解为 4 个组成部分:
等级 如果系列是直线,则为该系列的基线值。
趋势 系列随时间的可选且通常线性增加或减少的行为。
季节性 随着时间的推移,可选的重复模式或行为循环。
噪音 模型无法解释的观测值中的可选变异性。
所有时间序列都有一个等级,大多数都有噪音,趋势和季节性是可选的。
所有代码示例均使用 Python 编写并使用 Statsmodels 库。
时间序列预测方法
本文主要参考11种经典时间序列预测方法[1]
自回归 (Holt Winter, AR)
移动平均线 (Moving Average, MA)
自回归移动平均线 (Autoregressive Moving Average, ARMA)
自回归综合移动平均线 (Autoregressive Integrated Moving Average, ARIMA)
季节性自回归整合移动平均线 (Seasonal Autoregressive Integrated Moving-Average, SARIMA)
具有外生回归量的季节性自回归整合移动平均线 (Seasonal Autoregressive Integrated Moving-Average with Exogenous Regressors, SARIMAX)
向量自回归 (Vector Autoregression, VAR)
向量自回归移动平均 (Vector Autoregression Moving-Average, VARMA)
具有外源回归量的向量自回归移动平均值 (Vector Autoregression Moving-Average with Exogenous Regressors, VARMAX)
简单指数平滑 (Simple Exponential Smoothing, SES)
霍尔特·温特的指数平滑 (Holt Winter’s Exponential Smoothing, HWES)
01 自回归 (AR)
自回归 (AR) 方法将序列中的下一步建模为先前时间步长观测值的线性函数。
模型的符号涉及指定模型 的阶数作为 AR 函数的参数,例如 AR(p)。例如,AR(1) 是一阶自回归模型。
该方法适用于没有趋势和季节性成分的单变量时间序列。
定义
符号 表示 阶的自回归模型。模 型定义为:
在哪里 是模型的参数 , 是一个常数,并且 是白噪声。
在统计学、计量经济学和信号处理中,自回归 (AR) 模型是一种随机过程的表示;因此,它用于描述自然界、经济学等中的某些时变过程。自回归模型指定输出变量线性地取决于其自身先前的值和随机项(不完全可预测的项);因此该模型采用随机差分方程的形式(或不应与微分方程混淆的递推关系)。
与移动平均 (MA) 模型一起,它是更一般的时间序列自回归移动平均 (ARMA) 和自回归综合移动平均 (ARIMA) 模型的特例和关键组成部分,它们具有更复杂的随机结构体; 它也是向量自回归模型 (VAR) 的一个特例,它由一个包含多个互锁随机差分方程的系统组成,该系统包含多个演化随机变量。
更多内容可参见维基百科上的自回归模型[2]
Python代码
# AR example
from statsmodels.tsa.ar_model import AutoReg
from random import random
# contrived dataset
data = [x + random() for x in range(1, 100)]
# fit model
model = AutoReg(data, lags=1)
model_fit = model.fit()
# make prediction
yhat = model_fit.predict(len(data), len(data))
print(yhat)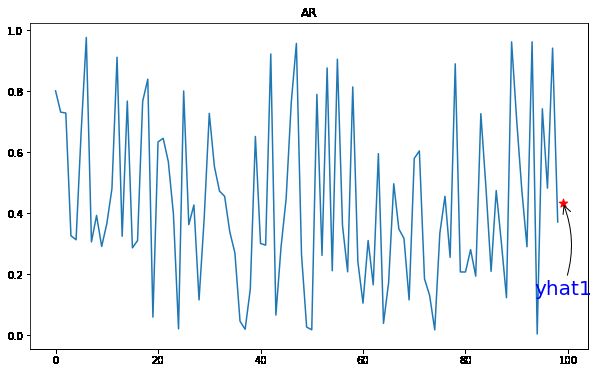
02 移动平均线 (MA)
移动平均(MA)方法将序列中的下一步建模为来自先前时间步骤的平均过程的残余误差的线性函数。
移动平均模型与计算时间序列的移动平均值不同。模型的符号包括指定模型的顺序 作为MA函数的参数,例如 MA(q)。例如,MA(1)是一阶移动平均模型。该方法适用于没有趋势和季节性成分的单变量时间序列。
定义
符号 是指顺序的移动平均模型 :
其中 是序列的平均值,θθ 是模型的参数,而 是白噪声误差项。 的值称为 MA 模型的阶数。
因此,移动平均模型在概念上是系列当前值与当前和先前(观察到的)白噪声误差项或随机冲击的线性回归。假设每个点的随机冲击是相互独立的,并且来自相同的分布,通常是正态分布,位置为零且尺度不变。
在时间序列分析中,移动平均线(MA)模型是对单变量时间序列建模的常用方法。MA模型指定输出变量线性取决于随机(不完全可预测)项的当前值和各种过去值。
与自回归 (AR) 模型 一起,MA模型是更一般的时间序列 ARMA 和 ARIMA 模型的特例和关键组件,它们具有更复杂的随机结构。
与 AR 模型相反,有限 MA 模型始终是静止的。
更多内容可参见 维基百科上的移动平均模型[3]
Python代码
我们可以使用 ARIMA 类来创建 MA 模型并设置零阶 AR 模型。我们必须在 order 参数中指定 MA 模型的顺序。
# MA example
from statsmodels.tsa.arima.model import ARIMA
from random import random
# contrived dataset
data = [random() for x in range(1, 100)]
# fit model
model = ARIMA(data, order=(0, 0, 1))
model_fit = model.fit()
# make prediction
yhat = model_fit.predict(len(data), len(data))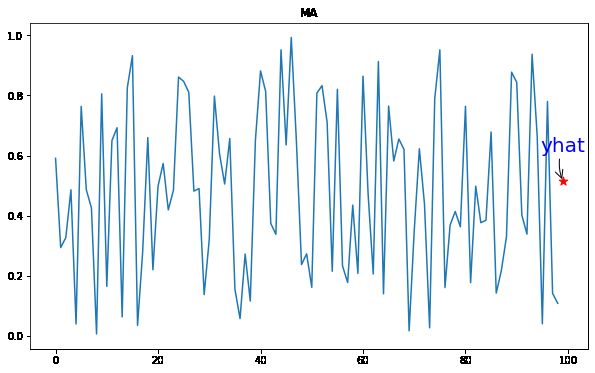
03 自回归移动平均线 (ARMA)
自回归移动平均 (ARMA) 方法将序列中的下一步建模为之前时间步骤的观测值和残差的线性函数。
它结合了自回归 (AR) 和移动平均 (MA) 模型。模型的符号涉及指定 和 模型的顺序作为 ARMA 函数的参数,例如 。ARIMA 模型可用于开发 AR 或 MA 模型。
该方法适用于没有趋势和季节性成分的单变量时间序列。
定义
符号 指的是具有 个自回归项和 个移动平均项的模型。该模型包含 和 模型,
在时间序列的统计分析中,自回归移动平均( ARMA )模型根据两个多项式提供了对(弱)平稳随机过程的简约描述,一个用于自回归(AR),第二个用于移动平均(嘛)。一般ARMA模型在1951年的论文中被描述彼得·惠特尔,在时间序列分析假设检验,它是在1970年的书普及乔治EP盒和格威利姆·詹金斯。
给定数据X t的时间序列,ARMA 模型是一种用于理解和预测该系列未来值的工具。AR 部分涉及根据其自己的滞后(即过去)值对变量进行回归。MA 部分涉及将误差项建模为过去不同时间同时发生的误差项的线性组合。
更多内容可参见维基百科上的自回归移动平均模型[4]
Python代码
# ARMA example
from statsmodels.tsa.arima.model import ARIMA
from random import random
# contrived dataset
data = [random() for x in range(1, 100)]
# fit model
model = ARIMA(data, order=(2, 0, 1))
model_fit = model.fit()
# make prediction
yhat = model_fit.predict(len(data), len(data))
print(yhat)04 自回归综合移动平均线 (ARIMA)
自回归整合移动平均(ARIMA)方法将序列中的下一步建模为先前时间步长的差异观测值和残差误差的线性函数。
它结合了自回归(AR)和移动平均(MA)模型以及序列的差分预处理步骤,使序列静止,称为积分(I)。
该模型的表示法涉及将 , 和 模型的顺序指定为 ARIMA 函数的参数,例如 ARIMA 函数的参数。 。ARIMA 模型也可用于开发 AR,MA 和 ARMA 模型。
该方法适用于具有趋势且没有季节性成分的单变量时间序列。
ARIMA的各个组成部分:
AR 部分 表示感兴趣的演化变量对其自身的滞后(即先验)值进行回归。
MA 部分 表示回归误差实际上是误差项的线性组合,其值同时发生在过去的不同时间。
I 部分 表示数据值已被替换为其值与先前值之间的差值(并且这个差值过程可能已经执行了不止一次)。这些特征中的每一个的目的都是使模型尽可能地拟合数据。
非季节性 ARIMA 模型通常表示为 其中参数 和 是非负整数, 是自回归模型的阶数(时间滞后数), 是差分(数据减去过去值的次数), 是移动平均模型的阶数。
季节性 ARIMA 模型通常表示为 ,其中 指的是每个季节的周期数,大写的 指的是 ARIMA 模型的季节性部分的自回归、差分和移动平均项。
更多内容可参见维基百科上的自回归综合移动平均线[5]
Python代码
# ARIMA example
from statsmodels.tsa.arima.model import ARIMA
from random import random
# contrived dataset
data = [random() for x in range(1, 100)]
# fit model
model = ARIMA(data, order=(1, 1, 1))
model_fit = model.fit()
# make prediction
yhat = model_fit.predict(len(data), len(data), typ='levels')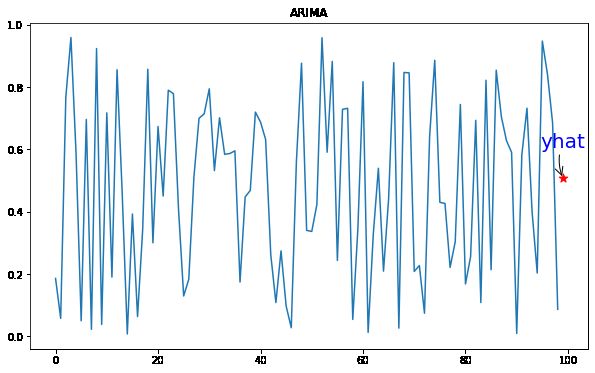
05 季节性自回归综合移动平均 (SARIMA)
季节ARIMA模型(SARIMA)方法模型序列中的下一步骤中用作差分观测的线性函数,错误,季节性求差的观察,和季节性的错误在先前时间的步骤。
它将 ARIMA 模型与在季节性水平上执行相同的自回归、差分和移动平均建模的能力相结合。
模型的符号包括指定 、和 模型的顺序作为 ARIMA 函数和 、、 和 的参数季节级别的参数。
例如 ,其中“m”是每个季节(季节期间)的时间步长数。SARIMA 模型可用于开发 AR、MA、ARMA 和 ARIMA 模型。
该方法适用于具有趋势和/或季节性成分的单变量时间序列。
ARIMA 模型有许多变体
如果使用多个时间序列,则 可以被认为是向量,此时 VARIMA 模型较为合适。
如果怀疑在模型中存在季节性效应,在这种情况下,通常认为使用 SARIMA(季节性ARIMA)模型比增加模型的 AR 或 MA 部分的阶数更好。
如果怀疑时间序列具有长期相关性,那么在自回归分数积分移动平均模型中可以允许 参数具有非整数值,该模型也称为分数 ARIMA(FARIMA 或 ARFIMA)) 模型。
Python代码
# SARIMA example
from statsmodels.tsa.statespace.sarimax import SARIMAX
from random import random
# contrived dataset
data = [random() for x in range(1, 100)]
# fit model
model = SARIMAX(data, order=(1, 1, 1), seasonal_order=(0, 0, 0, 0))
model_fit = model.fit(disp=False)
# make prediction
yhat = model_fit.predict(len(data), len(data))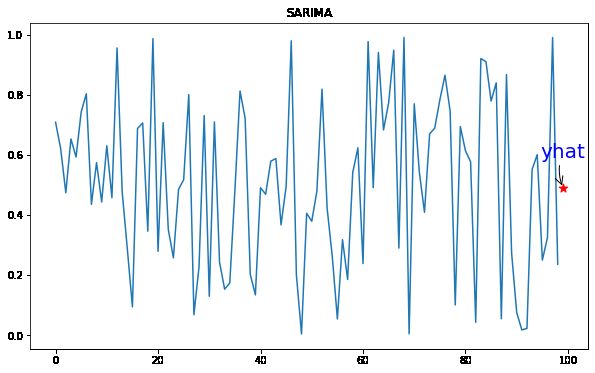
06 具有外生回归量的季节性自回归整合移动平均线(SARIMAX)
具有外源回归量的季节性自回归整合移动平均值(SARIMAX)是 SARIMA 模型的扩展,其还包括外生变量的建模。
外生变量也称为协变量,可以被认为是并行输入序列,其在与原始序列相同的时间步骤中具有观察结果。初级系列可以称为内源性数据,以将其与外源序列进行对比。对于外源变量的观察结果直接在每个时间步骤包括在模型中,并且不以与主要内源序列相同的方式建模(例如作为 AR,MA 等过程)。
SARIMAX 方法还可用于使用外生变量对包含的模型进行建模,例如 ARX、MAX、ARMAX 和 ARIMAX。
该方法适用于具有趋势和/或季节性成分和外生变量的单变量时间序列。
Python代码
# SARIMAX example
from statsmodels.tsa.statespace.sarimax import SARIMAX
from random import random
# contrived dataset
data1 = [x+random() for x in range(1, 100)]
data2 = [x+random() for x in range(101, 200)]
# fit model
model = SARIMAX(data1, exog=data2, order=(1, 1, 1), seasonal_order=(0, 0, 0, 0))
model_fit = model.fit(disp=False)
# make prediction
exog2 = [200+random()]
yhat = model_fit.predict(len(data1), len(data1), exog=[exog2])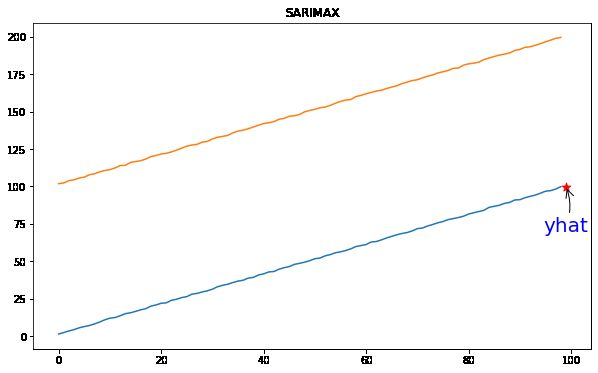
07 向量自回归 (VAR)
向量自回归(VAR)方法使用 AR 模型模拟每个时间序列中的下一步。AR 是多个并行时间序列的推广,例如,多变量时间序列。
该模型的符号涉及指定 模型的阶数作为 VAR 函数的参数,例如 。
该方法适用于没有趋势和季节性成分的多变量时间序列。
定义
VAR 模型描述了一组 个变量(称为内生变量)随时间的演变。每个时间段都有编号,
一般而言, 阶 VAR 是指包含最后 个时间段的滞后的 VAR 模型。 阶VAR模型表示为""。一个 阶 VAR 模型写为
表示变量在 个时间段之前的值,称为 的"第 个滞后" 。变量 是常数的 向量,用作模型的截距。 是时不变() 矩阵,而 是误差项的 向量。误差项必须满足三个条件:
每个误差项的均值为零。
误差项的同期协方差矩阵是一个 正半定矩阵,表示为 。
对于任何非零 ,跨时间没有相关性。特别是,在单个误差项中没有序列相关性。
矢量自回归(VAR) 是一种统计模型,用于捕捉随时间变化的多个数量之间的关系。VAR 是一种随机过程模型。VAR模型通过允许多变量时间序列来概括单变量(单变量)自回归模型。VAR 模型经常用于经济学和自然科学。
与自回归模型一样,每个变量都有一个方程来模拟其随时间的演变。该方程包括变量的滞后(过去)值、模型中其他变量的滞后值以及误差项。
VAR 模型不需要像具有联立方程的结构模型那样了解影响变量的力。唯一需要的先验知识是可以假设随着时间的推移相互影响的变量列表。
更多内容可参见维基百科上的向量自回归[6]
Python代码
# VAR example
from statsmodels.tsa.vector_ar.var_model import VAR
from random import random
# contrived dataset with dependency
data = list()
for i in range(100):
v1 = i + random()
v2 = v1 + random()
row = [v1, v2]
data.append(row)
# fit model
model = VAR(data)
model_fit = model.fit()
# make prediction
yhat = model_fit.forecast(model_fit.y, steps=1)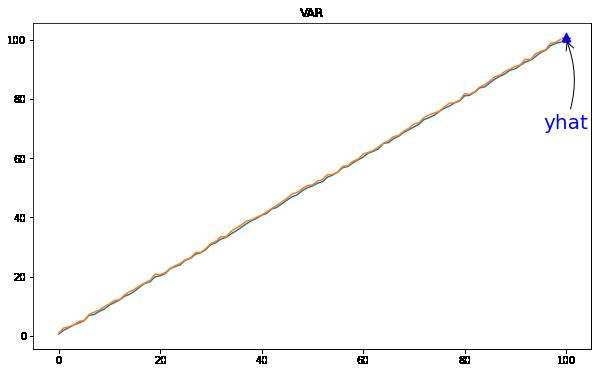
08 向量自回归移动平均值(VARMA)
向量自回归移动平均(VARMA)方法使用 ARMA 模型对每个时间序列中的下一步进行建模。这是 ARMA 对多个并行时间序列的推广,例如多变量时间序列。
该模型的表示法涉及将 和 模型的顺序指定为 VARMA 函数的参数,例如, 。VARMA 模型也可用于开发 VAR 或 VMA 模型。
该方法适用于没有趋势和季节性成分的多元时间序列。
Python代码
# VARMA example
from statsmodels.tsa.statespace.varmax import VARMAX
from random import random
# contrived dataset with dependency
data = list()
for i in range(100):
v1 = random()
v2 = v1 + random()
row = [v1, v2]
data.append(row)
# fit model
model = VARMAX(data, order=(1, 1))
model_fit = model.fit(disp=False)
# make prediction
yhat = model_fit.forecast()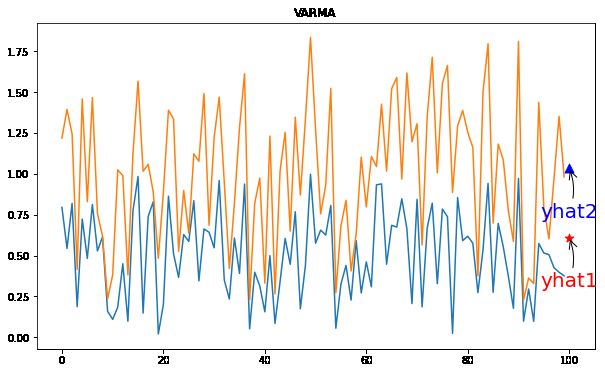
09 具有外源回归量的向量自回归移动平均值(VARMAX)
带有外生回归量的向量自回归移动平均 (VARMAX) 是 VARMA 模型的扩展,它还包括外生变量的建模。它是 ARMAX 方法的多元版本。
外生变量也称为协变量,可以被认为是并行输入序列,它们在与原始序列相同的时间步长中进行观察。主要系列被称为内源数据,以将其与外源序列进行对比。外生变量的观察值在每个时间步直接包含在模型中,并且不以与主要内生序列相同的方式建模(例如作为 AR、MA 等过程)。
VARMAX 方法还可用于对具有外生变量的包含模型进行建模,例如 VARX 和 VMAX。
该方法适用于具有外生变量的没有趋势和季节性成分的多元时间序列。
Python代码
# VARMAX example
from statsmodels.tsa.statespace.varmax import VARMAX
from random import random
# contrived dataset with dependency
data = list()
for i in range(100):
v1 = random()
v2 = v1 + random()
row = [v1, v2]
data.append(row)
data_exog = [x + random() for x in range(100)]
# fit model
model = VARMAX(data, exog=data_exog, order=(1, 1))
model_fit = model.fit(disp=False)
# make prediction
data_exog2 = [[100]]
yhat = model_fit.forecast(exog=data_exog2)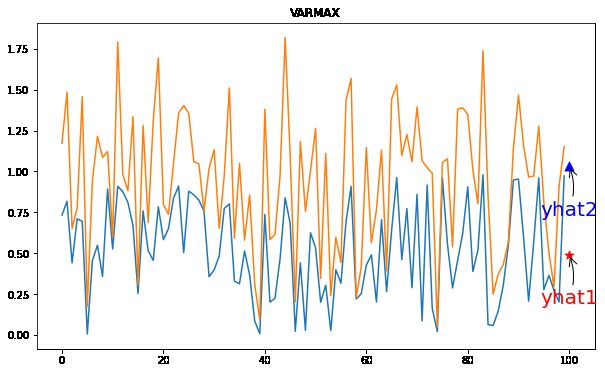
10 简单指数平滑 (SES)
简单指数平滑 (SES) 方法将下一个时间步建模为先前时间步观测值的指数加权线性函数。
该方法适用于没有趋势和季节性成分的单变量时间序列。
定义
指数平滑的最简单形式由以下公式给出:
式中 是平滑因子,并且 。换句话说,平滑的统计量 是当前观测值的简单加权平均值 和之前的平滑统计 。简单的指数平滑很容易应用,只要有两个观测值,它就会生成平滑的统计量。
平滑因子 具有较大的值,实际上降低平滑水平,并在极限情况下 输出系列只是当前的观察结果。
的值接近 1 的平滑效果较小,并且对数据中最近的变化给予更大的权重。
而 值 接近于零,具有更大的平滑效果并且对最近的变化的响应更小。
指数平滑是一种利用指数窗函数平滑时间序列数据的经验法则。而在简单的移动平均中,过去的观测值的权重是相等的。指数函数被用来分配随着时间呈指数递减的权重。
指数平滑是信号处理中常用的平滑数据的窗口函数之一,作为低通滤波器去除高频噪声。
更多内容可参见维基百科上的指数平滑[7]
Python代码
# SES example
from statsmodels.tsa.holtwinters import SimpleExpSmoothing
from random import random
# contrived dataset
data = [random() for x in range(1, 100)]
# fit model
model = SimpleExpSmoothing(data)
model_fit = model.fit()
# make prediction
yhat = model_fit.predict(len(data), len(data))
print(yhat)
11 霍尔特·温特的指数平滑(HWES)
Holt Winter 的指数平滑(HWES)也称为三次指数平滑方法,将下一个时间步长建模为先前时间步长的观测值的指数加权线性函数,并考虑趋势和季节性。
该方法适用于具有趋势和/或季节性分量的单变量时间序列。
Python代码
# HWES example
from statsmodels.tsa.holtwinters import ExponentialSmoothing
from random import random
# contrived dataset
data = [x + random() for x in range(1, 100)]
# fit model
model = ExponentialSmoothing(data)
model_fit = model.fit()
# make prediction
yhat = model_fit.predict(len(data), len(data))
参考资料
[1]
11种经典时间序列预测方法: https://machinelearningmastery.com/time-series-forecasting-methods-in-python-cheat-sheet/
[2]自回归模型: https://en.wikipedia.org/wiki/Autoregressive_model
[3]移动平均模型: https://en.wikipedia.org/wiki/Moving-average_model
[4]自回归移动平均模型: https://en.wikipedia.org/wiki/Autoregressive–moving-average_model
[5]自回归综合移动平均线: https://en.wikipedia.org/wiki/Autoregressive_integrated_moving_average
[6]向量自回归: https://en.wikipedia.org/wiki/Vector_autoregression
[7]指数平滑: https://en.wikipedia.org/wiki/Exponential_smoothing
往期精彩回顾
适合初学者入门人工智能的路线及资料下载机器学习及深度学习笔记等资料打印机器学习在线手册深度学习笔记专辑《统计学习方法》的代码复现专辑
AI基础下载黄海广老师《机器学习课程》视频课黄海广老师《机器学习课程》711页完整版课件本站qq群554839127,加入微信群请扫码:

