时序数据预测-Arima模型篇
ARIMA模型详解
- 基本概念
- ARIMA(p, d, q)预测模型
ARIMA差分整合移动平均自回归模型,用于时间序列数据分析与预测,相比ARMA模型在AR和MA之间多了差分步骤,目的是把非平稳序列转化为平稳序列,然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。其中p为偏相关图截尾的滞后阶数,是自回归AR的项数;d为平稳序列转非平稳序列所需的差分次数;q为预测误差的滞后值,即自相关图截尾的滞后阶数,是移动平均MA的项数,目的是使序列更光滑。
注:ARIMA模型要求时间序列数据满足平稳性和非白噪声(自相关系数接近0)。
差分可以提取非平稳确定性信息,但每次差分都会损失部分信息。
1.1 平稳序列的相关概念与检验
(1)平稳序列:序列的方差和均值为与时间无关的常数,协方差Cov(xt, xt-s)只与间隔s有关,
与t无关。(白噪声序列是平稳时间序列的一特例,要求均值与协方差为0)
(2) 非平稳序列:具有单位根,随着时间推进,数据无法回归给定值的趋势。
(3)单位根:序列的某个值等于前一个时期的对应值加上一个与之弱相关的干扰项。如果存在单位根,则可以通过差分来消除单位根,得到平稳序列。存在单位根的序列会表现出明显的记忆性和波动的持续性。
(4)平稳性转换的方法(由非平稳转换到平稳序列,实际具有三个方法)
①对数变换:减小数据振动幅度,使之线性规律更明显,相当于增加了处罚机制,数据越大惩罚越大。其中要求数据大于0。
②平滑法:移动平均法和指数平均法。
移动平均:利用一定时间间隔内的平均值作为某一期的估计值。
指数平均:不舍弃过去的数据,但仅给予逐渐减弱的影响程度/权值,即随着数据的远离,赋予逐渐收敛为零的权值。
③差分法(剔除周期性因素)
(5)平稳性检验:观察法和单位根检验法
①观察法:通过观察序列的趋势图与相关图是否随时间的变化呈现某种周期性的规律。线性周期可以用差分或者移动平均来解决,非线性周期需要一些分解方法。其中平稳序列的自相关系数会快速衰减。
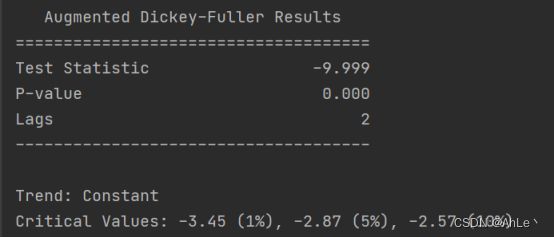
②单位根检验:即检验该差分方程(时间序列数据的方程)的特征方程的各个特征根是否小于1(即是否在单位圆内)。特征根小于1时才能满足方程特解收敛,从而满足稳定性条件。如果大于1,某一期的微小波动在未来会变得无穷大(方差会变得非常大),数据则无法预测。该检验可以使用ADF法(还有KPSS检验、PP检验),原假设为序列具有单位根,即非平稳,对于一个平稳的时序数据,需要在给定的置信水平上拒绝原假设。P值大于0.99则说明不能拒绝原假设。
P小于0.05,且test statistic的值同时小于5%和10%对应的值,则表明数据拒绝原假设,属于平稳序列。
差分方程:将某个时间序列变量表示为该变量的滞后项、时间和其他变量的函数,这样的函数方程被称为差分方程。
注:(为了帮助理解,特别引入以下两位知乎答主的答案,可作参考)
第一位:
第二位:
1.2 非白噪声(纯随机性)检验:利用下文1.7中的Q检验,当P小于0.05,则拒绝原假设,认为序列为非白噪声序列。
1.3 分解
将时序数据分离成不同的成分,主要是长期趋势,季节趋势和随机成分(残差)。得到不同的成分分解后,就可以使用时间序列模型对各个成分进行拟合。
目的:分解后的时序数据避免了各个成分在建模时的交叉影响,有助于提高预测的准确性。
1.4 AR(p)模型(P阶的自回归模型):必须具有平稳性和自相关性(自相关系数大于0.5)
(1)自回归:只适用于预测与自身历史因素相关的经济现象,对于受社会因素影响较大的经济现象不宜采用自回归,而应使用可纳入其他变量的向量自回归模型(多元时间序列)。
(2)AR模型描述当前值和历史值之间的关系。误差项εt是零均值白噪声序列,方程中系数项必须大于0.5,否则不宜采用该模型。
(3)P阶自回归:用之前的p个历史数值当作自变量。
1.5 MA(q)模型(q阶的移动平均过程):有效消除预测中的随机波动
(1)与AR模型不同的是MA模型要对误差项进行自回归。误差项εt是零均值白噪声序列。
(2)MA模型描述当前值和自回归部分误差累积的关系,其中q为常数时模型稳定。
(3)q阶移动平均:q是移动平均的项数。
1.6 p与q的确定
当代入p与q后得到的AIC、BIC、HQIC几个数值最小时,拟合模型效果最好。
过拟合问题:加入的参数个数越多,模型拟合效果越好,但却以提高模型复杂度为代价。因此,模型选择要在模型复杂度与模型拟合效果之间寻求最佳平衡。
(1)赤池信息准则AIC
AIC = 2x - 2lny
其中x为模型中参数的个数,反映模型复杂程度;y为模型的极大似然函数值,反映模型对数据的拟合程度。
(2)贝叶斯信息准则BIC
BIC = (lnT)x - 2lny
其中x,y的含义与AIC中相同,T为样本个数。
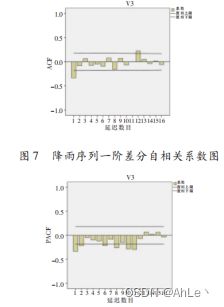
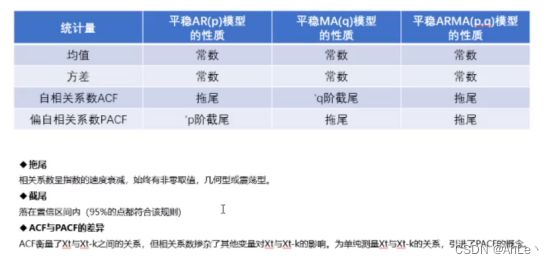
注:ACF自相关函数和PACF偏相关函数也可以用于确定ARIMA中p,q的阶数。(Y轴的值代表相关性:正相关,负相关(-1,1),X轴是lags滞后阶数。ACF反映同一序列在不同时序的取值之间的相关性。)
在区间外则代表存在相关性,白噪声全在区间内。
截尾:从x阶开始,所有点中有95%都落在置信区间内。
1.7 检验模型识别的完整性
为了检验该模型是否完全识别出时间序列数据的规律,引入Q检验。
(1)Q检验的功能:用于判断残差是否为白噪声序列,如果是,则代表模型已完全识别时序数据规律,模型可以被接受;如果否,则需要修正模型,例如剔除异常值。
此外还需检测残差是否满足正态分布(满足代表效果好)。
残差检验/相关性也可以看ACF,如果直接截尾则无相关性。
(2)Q检验/Ljung-Box检验的使用:
此处接受原假设,即p大于0.05,就代表序列为白噪声序列。
注:检验自相关性的方法还有D-W德宾沃森检验,接近2则不存在一阶自相关,接近0或4则存在自相关性。
1.8 逆变换
由于拟合的是经过预处理后的数据,因此预测值需要通过相关逆变换进行还原。一般会有多次差分还原,移动平均还原和对数还原。
1.9 拟合效果评估
此处使用均方根误差RMSE来评估拟合效果,此方法需要提出非预测数据的影响。
1.10 SARIMA模型:带季节性的ARIMA模型。
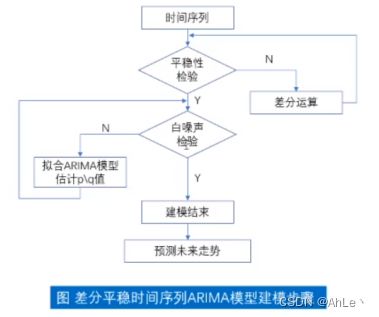
二、ARIMA模型的实践流程
获取数据→平稳性检验→d次差分→白噪声检验→确定p和q→残差检验→进行预测
三、时序数据与ARIMA 基础知识
(1)时间序列算子:将一个时间序列或一组时间序列变换成一个新的时间序列。
①乘法算子:y t= βxt
②加法算子:yt = xt + wt
③滞后算子:yt = xt-1 (一阶滞后)
(2)P阶滞后(差分方程):yt由yt-1到yt-p和wt(另一个变量)算出。
高斯白噪声过程:一个均值为0,方差σ²,各个ε之间独立的过程。
(3)移动平均过程:Y 由其历史中的残差序列组成
①一阶移动平均过程
Y t = μ + ε t + θεt-1 ,
其中θ和μ为任意常数,ε是白噪声残差序列。这个过程记作MA(1),之所以叫移动平均,是因为Y t是由最近两期ε的值的加权和构成的,类似一个平均。
②q阶移动平均过程MA(q):代表超过q阶滞后的自相关系数函数为0。
Y t = μ + ε t + θ1εt-1 +.....+ θ q ε t-q
其中θ依旧全是任意常数;
(4)自回归过程: Y 由其历史值组成
①一阶自回归过程AR(1)
Y t = c + φ Y t-1+ ε t ,
②p阶自回归AR(P)
Y t = c + φ1 Y t-1 + .... + φP Y t-P + ε t ,
(5)自回归综合移动平均过程ARMA:包含一个自回归和一个移动平均项
Y t = c + φ1 Y t-1 + .... + φP Y t-P + ε t + θ1εt-1 + ..... + θq ε t-q ,
注:ARIMA模型通常对单列时间序列数据进行预测,预测数据通常为5-15条。不管是训练数据还是预测数据,过长会影响预测效果。