使用python建立ARIMA模型

案例：2015/1/1至2015/2/6某餐厅销售数据进行建模
参考链接：
1.https://zhuanlan.zhihu.com/p/54985638
2.https://zhuanlan.zhihu.com/p/35128342
3.https://www.kaggle.com/pratyushakar/time-series-analysis-using-arima-sarima
statsmodels.tsa.arima_model文档：https://www.statsmodels.org/stable/search.html?q=statsmodels.tsa.arima_model
1：原始数据平稳性判断
2：差分数据平稳性判断
3：对差分数据建模，并得到预测值
4：返回原数据的预测值，并画出拟合图

import pandas as pd
import matplotlib.pyplot as plt  
from datetime import datetime   #数据索引改为时间
import numpy as np
import statsmodels.api as sm     #acf,pacf图
from statsmodels.tsa.stattools import adfuller  #adf检验
from pandas.plotting import autocorrelation_plot
from statsmodels.tsa.arima_model import ARIMA  

excelFile = 'C:/Users/admin/Desktop/Jupyter/数据分析/python数据分析-从入门到精通/第12周/arima_data.xls'
#读取数据，指定日期列为指标，Pandas自动将“日期”列识别为Datetime格式
data = pd.read_excel(excelFile, index_col = u'日期')
data = pd.DataFrame(data,dtype=np.float64)

#时序图
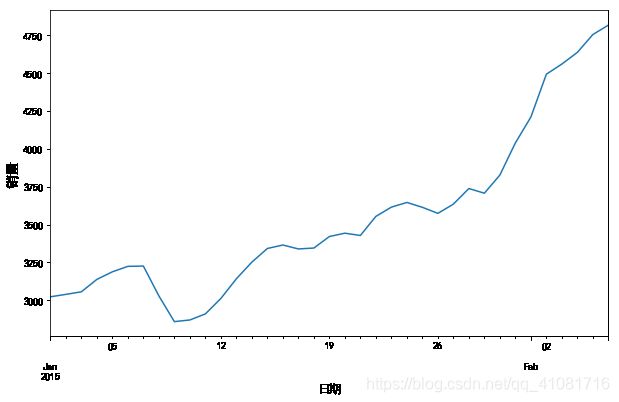
plt.figure(figsize=(10, 6))
plt.rcParams['font.sans-serif'] = ['SimHei']    #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False      #用来正常显示负号
data["销量"].plot()
plt.xlabel('日期',fontsize=12,verticalalignment='top')
plt.ylabel('销量',fontsize=14,horizontalalignment='center')
plt.show()

data.head()

	销量
日期
2015-01-01	3023.0
2015-01-02	3039.0
2015-01-03	3056.0
2015-01-04	3138.0
2015-01-05	3188.0

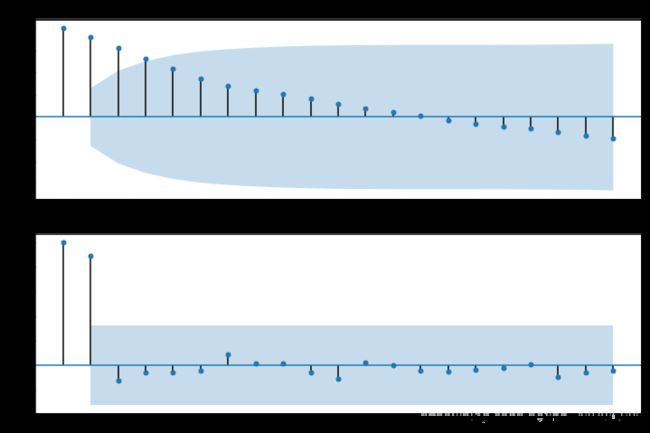
fig = plt.figure(figsize=(12,8))
ax1=fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(data,lags=20,ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(data,lags=20,ax=ax2)
plt.show()

#进行ADF检验

temp = np.array(data["销量"])
t = adfuller(temp)  # ADF检验
output=pd.DataFrame(index=['Test Statistic Value', "p-value", "Lags Used", "Number of Observations Used","Critical Value(1%)","Critical Value(5%)","Critical Value(10%)"],columns=['value'])
output['value']['Test Statistic Value'] = t[0]
output['value']['p-value'] = t[1]
output['value']['Lags Used'] = t[2]
output['value']['Number of Observations Used'] = t[3]
output['value']['Critical Value(1%)'] = t[4]['1%']
output['value']['Critical Value(5%)'] = t[4]['5%']
output['value']['Critical Value(10%)'] = t[4]['10%']
output

	value
Test Statistic Value	1.81377
p-value	0.998376
Lags Used	10
Number of Observations Used	26
Critical Value(1%)	-3.71121
Critical Value(5%)	-2.98125
Critical Value(10%)	-2.63009

# p值0.998,即可以认为非平稳
#ADF检验的原假设是存在单位根，只要这个统计值是小于1%水平下的数字就可以极显著的拒绝原假设，认为数据平稳
#https://www.lizenghai.com/archives/595.html

#白噪声检验

# 白噪声检验（如果是白噪声，即纯随机序列，则没有研究的意义了。）
from statsmodels.stats.diagnostic import acorr_ljungbox
print(acorr_ljungbox(data["销量"], lags=1)) 

(array([ 32.0111333]), array([  1.53291527e-08]))

#返回统计量和p值
# 原假设是序列为白噪声，所以p值为1.53291527e-08，表明序列为非白噪声序列

#差分

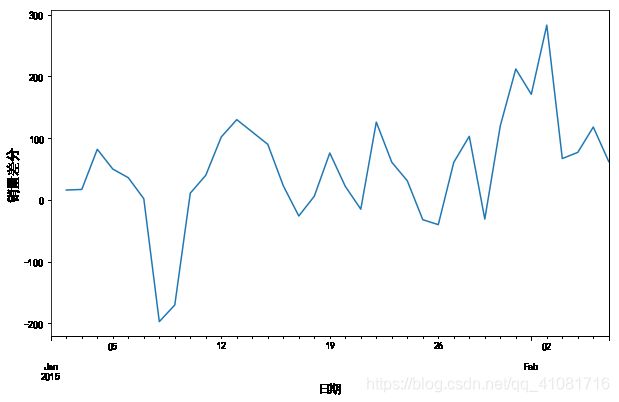
data1= data["销量"].diff(1)
plt.figure(figsize=(10, 6))
data1.plot()
plt.xlabel('日期',fontsize=12,verticalalignment='top')
plt.ylabel('销量差分',fontsize=14,horizontalalignment='center')
plt.show()

#差分序列的ADF平稳性检验

temp = np.diff(data["销量"])
t = adfuller(temp)  # ADF检验
output=pd.DataFrame(index=['Test Statistic Value', "p-value", "Lags Used", "Number of Observations Used","Critical Value(1%)","Critical Value(5%)","Critical Value(10%)"],columns=['value'])
output['value']['Test Statistic Value'] = t[0]
output['value']['p-value'] = t[1]
output['value']['Lags Used'] = t[2]
output['value']['Number of Observations Used'] = t[3]
output['value']['Critical Value(1%)'] = t[4]['1%']
output['value']['Critical Value(5%)'] = t[4]['5%']
output['value']['Critical Value(10%)'] = t[4]['10%']
output

	value
Test Statistic Value	-3.15606
p-value	0.0226734
Lags Used	0
Number of Observations Used	35
Critical Value(1%)	-3.63274
Critical Value(5%)	-2.94851
Critical Value(10%)	-2.61302

# 看到 t-statistic 的值-3.156要小于5%，所以拒绝原假设，另外，p-value的值0.02也很小。

#将差分序列改为与原始数据相同的数据格式

sales = list(np.diff(data["销量"]))
data2 = {
    "日期":data1.index[1:],  #1月1日是空值，从1月2号开始取
    "销量":sales
}
df = pd.DataFrame(data2)
df['日期'] = pd.to_datetime(df['日期']) 
#df[''date]数据类型为“object”，通过pd.to_datetime将该列数据转换为时间类型，即datetime。 
data_diff = df.set_index(['日期'], drop=True)    
#将日期设置为索引
data_diff.head()

	销量
日期
2015-01-02	16.0
2015-01-03	17.0
2015-01-04	82.0
2015-01-05	50.0
2015-01-06	36.0

#差分序列的acf,pacf

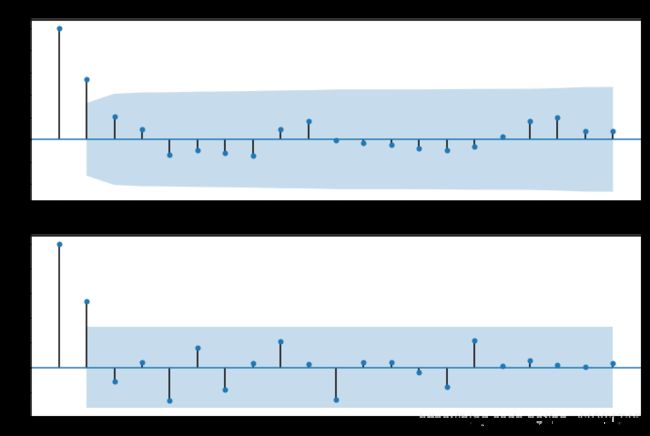
fig = plt.figure(figsize=(12,8))
ax1=fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(data_diff,lags=20,ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(data_diff,lags=20,ax=ax2)
plt.show()

#模型定阶：AIC,BIC,或者根据acf,pacf图

# 为了控制计算量，我们限制AR最大阶不超过6，MA最大阶不超过4。
sm.tsa.arma_order_select_ic(data_diff,max_ar=6,max_ma=4,ic='aic')['aic_min_order']  # AIC




    (0, 1)




```python
#BIC

#对模型进行定阶
pmax = int(len(df) / 10)    #一般阶数不超过 length /10
qmax = int(len(df) / 10)
bic_matrix = []
for p in range(pmax +1):
    temp= []
    for q in range(qmax+1):
        try:
            temp.append(ARIMA(data, (p, 1, q)).fit().bic)
        except:
            temp.append(None)
        bic_matrix.append(temp)

bic_matrix = pd.DataFrame(bic_matrix)   #将其转换成Dataframe 数据结构
p,q = bic_matrix.stack().idxmin()   #先使用stack 展平， 然后使用 idxmin 找出最小值的位置
print(u'BIC 最小的p值 和 q 值：%s,%s' %(p,q))  #  BIC 最小的p值 和 q 值：0,1
#所以可以建立ARIMA 模型，ARIMA(0,1,1)

BIC 最小的p值 和 q 值：0,1

#具体模型信息

model = ARIMA(data, (p,1,q)).fit()
model.summary2()        #生成一份模型报告

Model:	ARIMA	BIC:	422.5101
Dependent Variable:	D.销量	Log-Likelihood:	-205.88
Date:	2020-04-27 22:21	Scale:	1.0000
No. Observations:	36	Method:	css-mle
Df Model:	2	Sample:	01-02-2015
Df Residuals:	34		02-06-2015
Converged:	1.0000	S.D. of innovations:	73.086
AIC:	417.7595	HQIC:	419.418

	Coef.	Std.Err.	t	P>|t|	[0.025	0.975]
const	49.9564	20.1390	2.4806	0.0182	10.4847	89.4281
ma.L1.D.销量	0.6710	0.1648	4.0712	0.0003	0.3480	0.9941

	Real	Imaginary	Modulus	Frequency
MA.1	-1.4902	0.0000	1.4902	0.5000

predictions_ARIMA_diff = pd.Series(model.fittedvalues, copy=True)
print(predictions_ARIMA_diff.head())

日期
2015-01-02    49.956427
2015-01-03    34.245128
2015-01-04    39.803780
2015-01-05    76.789439
2015-01-06    32.393775
dtype: float64

plt.figure(figsize=(10, 6))
plt.plot(predictions_ARIMA_diff,label="forecast_diff")
plt.plot(data_diff,label="diff")
plt.xlabel('日期',fontsize=12,verticalalignment='top')
plt.ylabel('销量差分',fontsize=14,horizontalalignment='center')
plt.legend()
plt.show()

#注意这里差分预测值和实际数据有日期错位，所以要进行修改

predictions = [i + j for i, j in zip(list(predictions_ARIMA_diff), list(data["销量"][:36]))]

prediction_sales = {
    "日期":data1.index[1:],
    "销量":predictions
}
prediction_sales = pd.DataFrame(prediction_sales)
prediction_sales['日期'] = pd.to_datetime(prediction_sales['日期']) 
#df[''date]数据类型为“object”，通过pd.to_datetime将该列数据转换为时间类型，即datetime。 
prediction_sales = prediction_sales.set_index(['日期'], drop=True)    
#将日期设置为索引
prediction_sales.head()

	销量
日期
2015-01-02	3072.956427
2015-01-03	3073.245128
2015-01-04	3095.803780
2015-01-05	3214.789439
2015-01-06	3220.393775

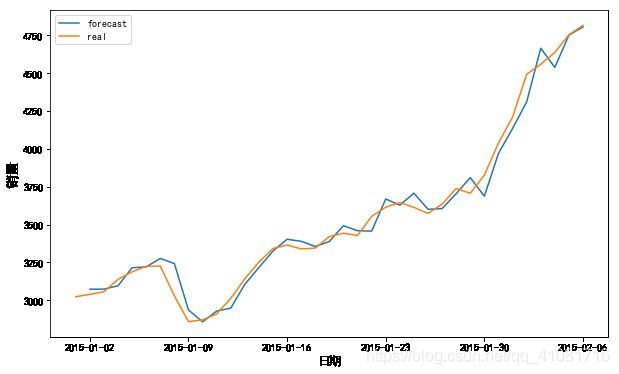
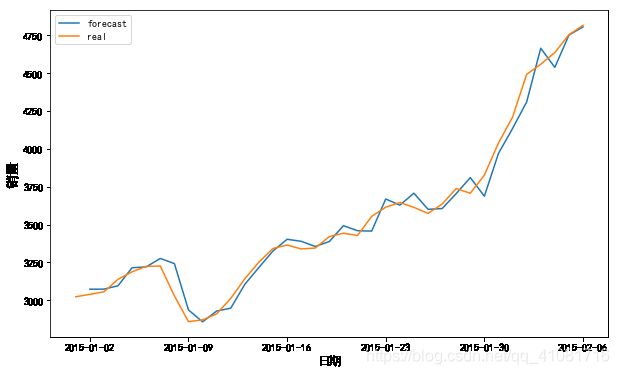
plt.figure(figsize=(10, 6))
plt.plot(prediction_sales,label="forecast")
plt.plot(data,label="real")
plt.xlabel('日期',fontsize=12,verticalalignment='top')
plt.ylabel('销量',fontsize=14,horizontalalignment='center')
plt.legend()
plt.show()

model.forecast(5)   #为未来5天进行预测， 返回预测结果， 标准误差， 和置信区间

(array([ 4873.9667493 ,  4923.92317644,  4973.87960359,  5023.83603073,
         5073.79245787]),
 array([  73.08574293,  142.32679918,  187.542821  ,  223.80281869,
         254.95704265]),
 array([[ 4730.72132537,  5017.21217324],
        [ 4644.96777602,  5202.87857687],
        [ 4606.30242887,  5341.4567783 ],
        [ 4585.19056646,  5462.48149499],
        [ 4574.08583666,  5573.49907907]])