量子计算 7 超密编码与量子遥传
密集编码与量子遥传
- 1 超密编码(Superdense Coding)
-
- 1.1 Holevo's Theorem
- 1.2 密集编码
- 2 量子遥传/量子隐形传态(Quantum teleportation)
-
- 2.1 量子遥传
- 2.2 量子遥传分析
- 3 Multi-Qubit Teleportation and Entanglement Swapping
- 4 小结
- 5 附录: 几个常用门 X, Z, SWAP
量子会给信息的编码和传输方式带来什么惊喜呢?根据香农的信息论,通过发送 n n n个比特,只能传递不超过 n n n比特的信息,似乎这是句废话,但是使用量子纠缠,我们好像可以打破这个限制,这就是超密编码要告诉我们的内容,通过发送一个量子比特可以传递两个经典比特的信息。而如何通过经典信息通道传输一个量子比特的技术即量子遥传或量子隐形传态。
1 超密编码(Superdense Coding)
1.1 Holevo’s Theorem
密集编码有一个前提条件,即需要事先具有纠缠的量子比特;如果没有纠缠的量子比特,发送一个量子比特也只能传递一个经典比特的信息。
或许我们会想,一个量子态 ∣ ψ ⟩ = α ∣ 0 ⟩ + β ∣ 1 ⟩ |\psi\rangle=\alpha|0\rangle+\beta|1\rangle ∣ψ⟩=α∣0⟩+β∣1⟩的系数即量子幅是一个复数,那按理来说只要其是个无限位小数,那一个数就可以把四大名著都存储进去,但是,需要注意的是,我们在一次测量之后就由于坍塌失去了其余所有信息;这就像,通过一个硬币的正反面概率同样可以编码四大名著一样,但是我们要通过无数次测量才能获得这个精确的概率,而对量子比特来说,根据不可克隆定理,这样是做不到的。
即使具备纠缠的量子比特,每发送一个量子比特,最多也只能传递两个经典比特的信息。
1.2 密集编码
假设张三李四分布持有Bell pair ∣ ψ ⟩ = ∣ 00 ⟩ + ∣ 11 ⟩ 2 |\psi\rangle=\frac{|00\rangle+|11\rangle}{\sqrt{2}} ∣ψ⟩=2∣00⟩+∣11⟩的第一个和第二个量子比特,那么张三通过操作自己的这个比特,然后将其发送给李四,那么李四通过测量收到的和自己持有的这两个量子比特,就可以通过发送一个量子比特获得两个经典比特的信息,现在来看看该怎么办。
首先,张三通过操作自己的第一个量子比特,可以获得四个量子态,其中 X X X门和 Z Z Z门如附录所示:

当然,第四个量子态就是Bell pair ∣ ψ ⟩ = ∣ 00 ⟩ + ∣ 11 ⟩ 2 |\psi\rangle=\frac{|00\rangle+|11\rangle}{\sqrt{2}} ∣ψ⟩=2∣00⟩+∣11⟩本身,通过内积运算,我们可以验证,这四个量子态是正交的。
于是,这四个量子态可以对应两个经典比特 x x x和 y y y,假如 x = 1 x=1 x=1则张三实施 X X X门操作,加如 y = 1 y=1 y=1则张三实施 Z Z Z门操作。
然后,张三把自己的量子比特发送给李四,那李四就得到了这四个可能的量子态。李四可以进行如下的骚操作:

该量子电路对应得矩阵为:

其先以第二个量子比特为控制比特进行CNOT门操作,然后进行 H H H门操作。可以得知,这四个量子态经过该骚操作后:
∣ 00 ⟩ + ∣ 11 ⟩ 2 → ∣ 00 ⟩ + ∣ 01 ⟩ 2 = ∣ 0 + ⟩ 2 → ∣ 00 ⟩ 2 ∣ 01 ⟩ + ∣ 10 ⟩ 2 → ∣ 11 ⟩ + ∣ 10 ⟩ 2 = ∣ 1 + ⟩ 2 → ∣ 10 ⟩ 2 ∣ 00 ⟩ − ∣ 11 ⟩ 2 → ∣ 00 ⟩ − ∣ 01 ⟩ 2 = ∣ 0 − ⟩ 2 → ∣ 01 ⟩ 2 ∣ 01 ⟩ − ∣ 10 ⟩ 2 → ∣ 11 ⟩ − ∣ 10 ⟩ 2 = ∣ 1 − ⟩ 2 → ∣ 11 ⟩ 2 \frac{|00\rangle+|11\rangle}{\sqrt{2}}\rightarrow \frac{|00\rangle+|01\rangle}{\sqrt{2}} =\frac{|0+\rangle}{\sqrt{2}} \rightarrow \frac{|00\rangle}{\sqrt{2}} \\ \frac{|01\rangle+|10\rangle}{\sqrt{2}}\rightarrow \frac{|11\rangle+|10\rangle}{\sqrt{2}} =\frac{|1+\rangle}{\sqrt{2}} \rightarrow \frac{|10\rangle}{\sqrt{2}} \\ \frac{|00\rangle-|11\rangle}{\sqrt{2}}\rightarrow \frac{|00\rangle-|01\rangle}{\sqrt{2}} =\frac{|0-\rangle}{\sqrt{2}} \rightarrow \frac{|01\rangle}{\sqrt{2}}\\ \frac{|01\rangle-|10\rangle}{\sqrt{2}}\rightarrow \frac{|11\rangle-|10\rangle}{\sqrt{2}} =\frac{|1-\rangle}{\sqrt{2}} \rightarrow \frac{|11\rangle}{\sqrt{2}} 2∣00⟩+∣11⟩→2∣00⟩+∣01⟩=2∣0+⟩→2∣00⟩2∣01⟩+∣10⟩→2∣11⟩+∣10⟩=2∣1+⟩→2∣10⟩2∣00⟩−∣11⟩→2∣00⟩−∣01⟩=2∣0−⟩→2∣01⟩2∣01⟩−∣10⟩→2∣11⟩−∣10⟩=2∣1−⟩→2∣11⟩
于是,李四通过测量张三传递过来的量子比特和自己所持有的量子比特可以获得两个经典比特的信息。
2 量子遥传/量子隐形传态(Quantum teleportation)
那么,如何传递一个量子比特呢?量子遥传或者量子隐形传态(Quantum teleportation)可以通过经典信息通道和纠缠的量子比特来发送量子比特。且通过一个纠缠的量子比特和发送两个经典比特,只能实现一个量子比特的传送。
2.1 量子遥传
首先肯定是张三李四有个Bell pair ∣ 00 ⟩ + ∣ 11 ⟩ 2 \frac{|00\rangle+|11\rangle}{\sqrt{2}} 2∣00⟩+∣11⟩,然后张三有个量子态 ∣ ψ ⟩ |\psi\rangle ∣ψ⟩,然后注意了,张三的骚操作如下所示:

简单说,张三以 ∣ ψ ⟩ |\psi\rangle ∣ψ⟩为控制对自己手里的纠缠比特作CNOT门操作,然后对 ∣ ψ ⟩ |\psi\rangle ∣ψ⟩作H门操作,这样就会有以下运算:
首先张三和李四的量子比特如下所示:

CNOT操作后:
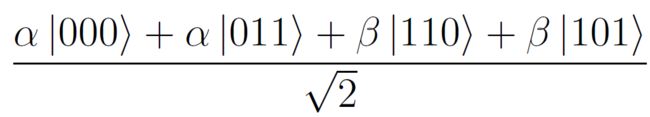
经过H门操作:

于是,张三会测量第一个和第二个量子比特,观测到的结果,对应的李四手里的量子比特为:

于是,张三把观测结果告诉李四,如果张三的第一个比特结果为1,那李四就进行Z门操作,如果张三的第二个比特是1,那李四就进行X门操作,于是,李四手中纠缠的量子比特就变成了 ∣ ψ ⟩ = α ∣ 0 ⟩ + β ∣ 1 ⟩ |\psi\rangle=\alpha |0\rangle+\beta |1\rangle ∣ψ⟩=α∣0⟩+β∣1⟩,于是 ∣ ψ ⟩ |\psi\rangle ∣ψ⟩就从张三手里发送到了李四手里,所需要的条件是一个纠缠的Bell pair和发送两个经典比特。
2.2 量子遥传分析
根据不可克隆定理(No-Clong Theorem) 可以理解,张三在发送完 ∣ ψ ⟩ |\psi\rangle ∣ψ⟩之后,自己就没有 ∣ ψ ⟩ |\psi\rangle ∣ψ⟩了,而根据No-Communication theorem我们可以知道,在不发送这两个经典比特的时候,李四不可能接收到这个量子比特 ∣ ψ ⟩ |\psi\rangle ∣ψ⟩,也就是李四的密度矩阵仍然是上面四个量子态的均匀混合mixture。
3 Multi-Qubit Teleportation and Entanglement Swapping
刚发送过去的 ∣ ψ ⟩ |\psi \rangle ∣ψ⟩也可以是另一个bell pair的量子比特,那又可以进行下一个量子态传输。于是,通过 n n n个纠缠的量子比特和发送 2 n 2n 2n个经典比特,可以实现 n n n个量子比特的传输。
另一个发现是,两个量子比特要发生纠缠不需要直接作用,如以下电路所示:

见附录里面的SWAP门。这一通操作可以让第一个和第三个比特发生纠缠,而第二个比特起到了中介的作用。
Entanglement Swapping
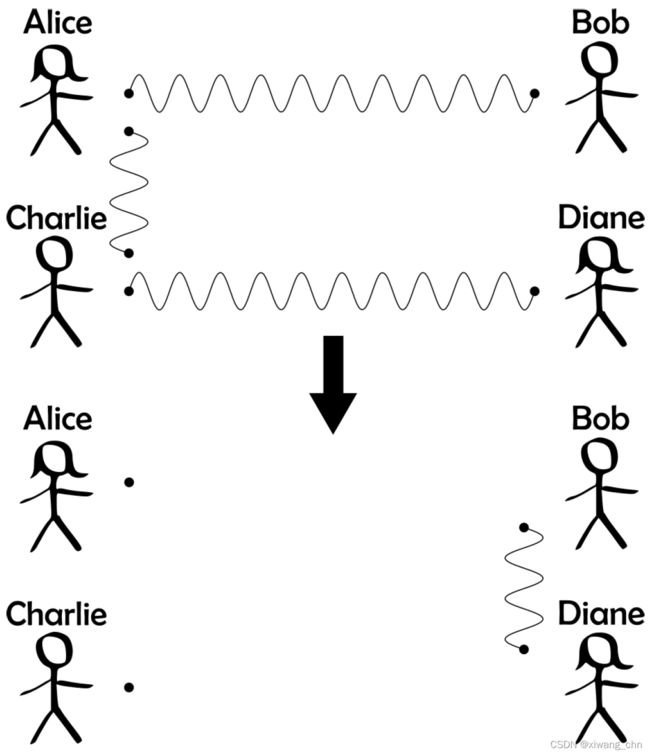
通过量子遥传,可以把纠缠的量子比特从这俩人转到另外两人,很简单的理解,所传递的 ∣ ψ ⟩ |\psi\rangle ∣ψ⟩可以和别的比特是纠缠的,因此把纠缠的两个比特分别通过量子遥传到另一对同学手里面,就实现了Entanglement Swapping。
4 小结
量子遥传结合前面的超密编码,你是不是发现,前面说发送一个量子比特可以传递两个经典比特的信息,后面又说,发送一个量子比特需要发送俩经典比特,真是一通操作猛如虎,一看结果操作了个寂寞。
不过呢,这里的好处是,即使你窃听了所传送的经典比特,你也不知道真正的量子态,因为这个纠缠的量子比特还在李四手里面,而你如果直接去观察该量子比特,就会发生坍塌,也就回到了之前 量子比特 6 里面窃听风云的分析了。所以只能这么说,超密编码和量子遥传是两个侧重点不同的应用,非要一起用不能实现发送一个实现两个信息的传输的作用,只能说可以在保密性上作很大的文章了。

