相机标定篇——相机标定

认为相机标定是三维重建的核心，研究生期间主要方向为结构光三维重建

必要的数学知识

线性方程求解
Gauss消元法；LU分解；Cholesky分解
最小二乘问题-线性方法
特征值分解；奇异值分解；超定线性方程；最小二乘SVD法
最小二乘问题-非线性优化
最速下降；牛顿法；高斯牛顿法；LM优化；

单相机标定

目前相机标定有很多成熟的算法库如Opencv或者matlab工具箱以及Halcon，其中matlab与halcon貌似做的精度会相对高一些，但是实际工程中，上述平台的标定算法的灵活度较低，因此往往是自己开发算法。
相机标定，目的是确定相机的内参矩阵K、外参矩阵R t和 畸变系数 d 。

四大坐标系

世界坐标系->相机坐标系

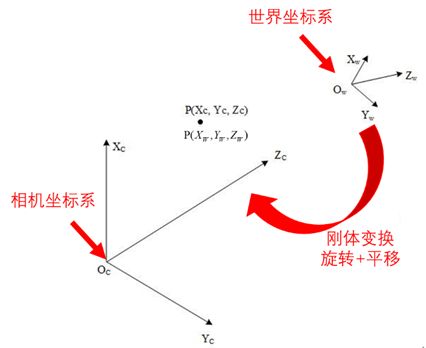
世界坐标系：以外界某个参考点建立的坐标系，单位为 $mm$，或者 $m$
相机坐标系：以相机光心建立的坐标系，其 $z$ 轴指向相机的正前方。

假设物点在世界坐标系下的坐标为：$P=[X_W,Y_W,Z_W]$，那么转换到相机坐标系下坐标：$P=[X_C,Y_C,Z_C{]}^T$ 的变换如下

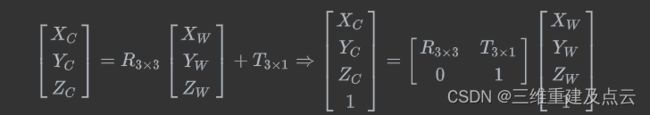
相机坐标系->图像坐标系

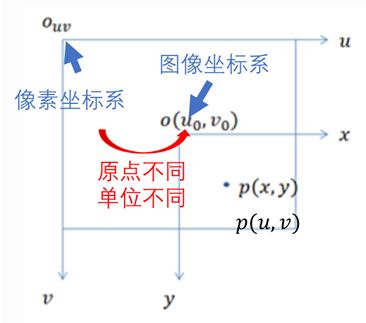
我们用 $u,v$ 来记像素的列数与行数，那么：

• 图像坐标系下的坐标系原点，在像素坐标系 $u-v$ 下记为：$o(u_0,v_0)$
• 像点 $p$，在 $u-v$ 坐标系下记为：$p(u,v)$

此外，再分别记 $dx,dy$ 为每个像素在 $x$ 轴、$y$ 轴所代表的物理尺寸大小，可推导出下式

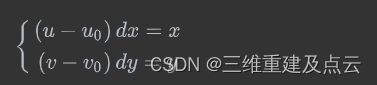
将上式写成齐次的形式有

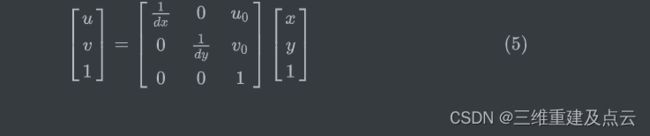
汇总

四大坐标系转换关系

张正友标定法

张正友标定法利用如下图所示的棋盘格标定板，在得到一张标定板的图像之后，可以利用相应的图像检测算法得到每一个角点的像素坐标 (u,v)。

张正友标定法将世界坐标系固定于棋盘格上，则棋盘格上任一点的物理坐标 W=0，由于标定板的世界坐标系是人为事先定义好的，标定板上每一个格子的大小是已知的，我们可以计算得到每一个角点在世界坐标系下的物理坐标(U,V,W=0)。
我们将利用这些信息：每一个角点的像素坐标 (u,v) 、每一个角点在世界坐标系下的物理坐标(U,V,W=0)，来进行相机的标定，获得相机的内外参矩阵、畸变参数。

标定相机的内参矩阵和外参矩阵

思路如下：①求解内参矩阵与外参矩阵的积； ②求解内参矩阵； ③求解外参矩阵

求解内参矩阵与外参矩阵的积

将世界坐标系固定于棋盘格上，则棋盘格上任一点的物理坐标 W=0 ，因此，原单点无畸变的成像模型可以化为下式。其中， R1,R2为旋转矩阵 R 的前两列。为了简便，将内参矩阵记为A。

对于不同的图片，内参矩阵A 为定值；对于同一张图片，内参矩阵A，外参矩阵(R1,R2,T)为定值；对于同一张图片上的单点，内参矩阵A，外参矩阵 (R1,R2,T)，尺度因子 Z为定值。
我们将 A(R1 R2 T)记为矩阵 H ， H 即为内参矩阵和外参矩阵的积，记矩阵 H 的三列为 [H1 H2 H3] ，则有：

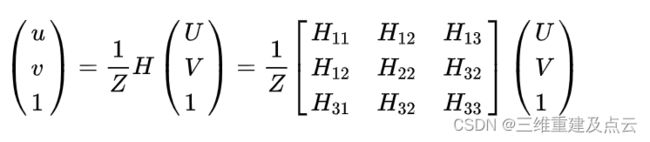
利用上式消去尺度因子Z可得

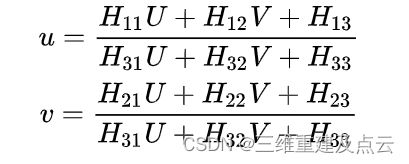
上式对于同一张图片上所有的角点均成立。（u,v）是像素坐标系下的标定板角点的坐标， (UV) 是世界坐标系下的标定板角点的坐标。通过图像识别算法，我们可以得到标定板角点的像素坐标（u,v），又由于标定板的世界坐标系是人为定义好的，标定板上每一个格子的大小是已知的，我们可以计算得到世界坐标系下的(UV) 。

由这里的H 是齐次矩阵，有8个独立未知元素。每一个标定板角点可以提供两个约束方程（u,UV的对应关系、 v,UV的对应关系提供了两个约束方程），因此，当一张图片上的标定板角点数量等于4时，即可求得该图片对应的矩阵H。当一张图片上的标定板角点数量大于4时，利用最小二乘法回归最佳的矩阵 H。

求解内参矩阵

目前已知了H=A(R1 R2 T)，下面求解内参A 利用R1R2的单位正交关系


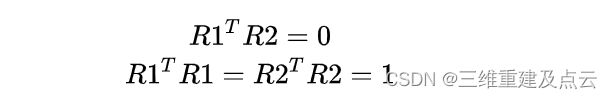
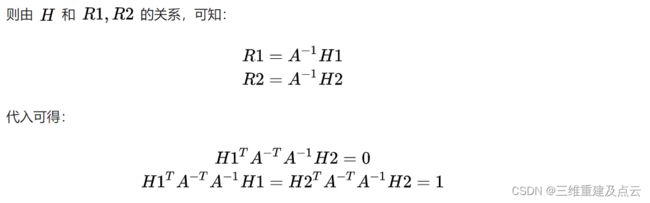
为了简便，记相机内参矩阵A为


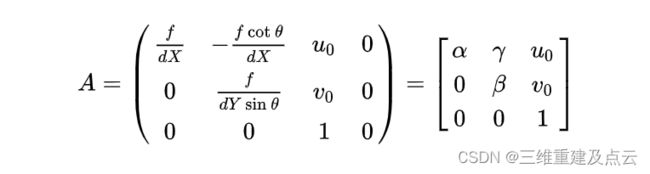
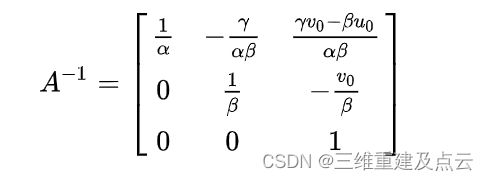
则用矩阵 A表示矩阵B得：

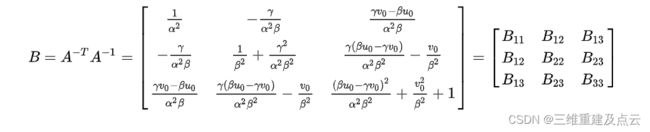
B为对称阵，B12 B13 B23 出现了两次
使用B=A-TA-1，将前面的单位正交约束方程化为


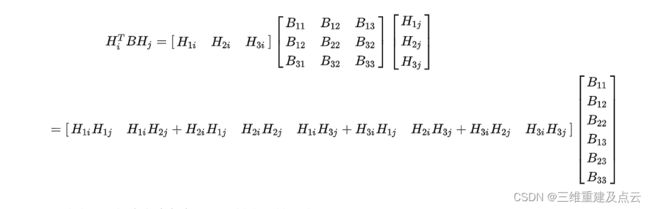
此时，通过 R1,R2单位正交得到的约束方程可化为

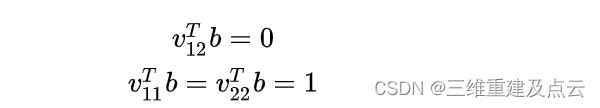
写成矩阵的形式

由于矩阵H已知，矩阵v又全部由矩阵H的元素构成，因此矩阵v已知。

此时，我们只要求解出向量 b ，即可得到矩阵 B 。每张标定板图片可以提供一个 vb=0的约束关系，该约束关系含有两个约束方程。但是，向量b有6个未知元素。因此，单张图片提供的两个约束方程是不足以解出来向量b。因此，我们只要取3张标定板照片，得到3个vb=0的约束关系，即6个方程，即可求解向量 b。当标定板图片的个数大于3时（事实上一般需要15到20张标定板图片），可采用最小二乘拟合最佳的向量b，并得到矩阵B

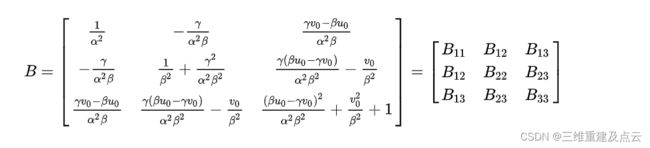
求解外参

上述过程已经求出了H，内参A ，通过公式(R1 R2 T)=A-1H 即可求得每一张图片对应的外参矩阵（R1 R2 T）
此时相机的内参与外参均已得到

畸变参数

张正友标定只考虑了径向畸变
径向畸变公式（2阶）如下：
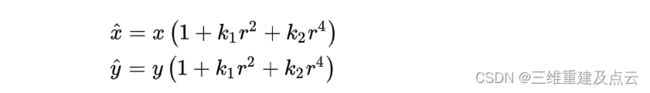分别为理想的无畸变的归一化的图像坐标、畸变后的归一化图像坐标
r为图像像素点到图像中心点的距离.
图像坐标和像素坐标的转化关系为：

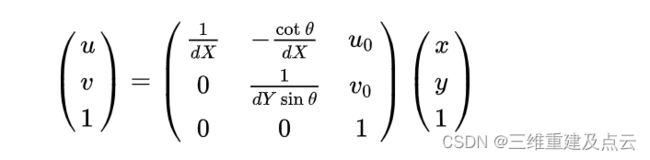
同理可得畸变后的像素坐标的表达式为

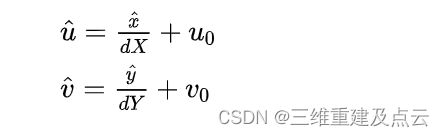
代入径向畸变公式（2阶）则有：


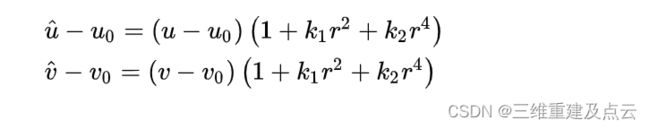
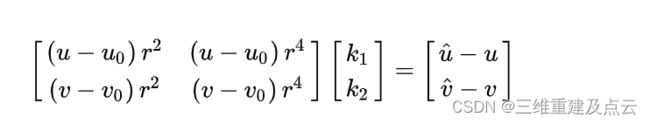
上式中的uv可以通过识别标定板的角点获得，每一个角点可以构造两个上述等式。有m幅图像，每幅图像上有n个标定板角点，则将得到的所有等式组合起来，可以得到个mn未知数为的 k[k1,k2]T 约束方程，将约束方程系数矩阵记为D，等式右端非齐次项记为 d ，可将其记着矩阵形式：

则使用最小二乘法可求得：

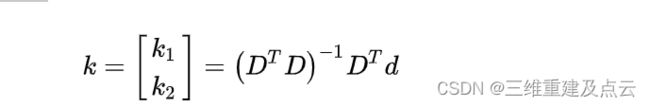
LM算法参数优化

从上述推导过程就可以看出，张正友标定法是有很多近似的，所以仅仅利用上述的过程进行标定误差肯定是很大的。所以张正友标定法还利用L-M（Levenberg-Marquardt）算法对参数进行了优化。下一篇博客更新LM算法