强化学习之第一篇：基础知识点学习

记录自己学习强化学习的笔记。
从b站王树森教授的视频开始：视频链接 https://www.bilibili.com/video/BV12o4y197US/?spm_id_from=333.337.search-card.all.click

强化学习

基本概念

0、一些名词

transition：一次 transition 就是执行一次下列过程，对当前状态 $s$，选取动作 $a$ 后，进入下一时刻状态$s\prime$ ，拿到奖励 $r$；可以表示为 $(s,a,r,s\prime )$ ，加入时间的话可以表示为 $(s_t,a_t,r_t,s_{t+1})$。

episode：一次episode就是一套完整的决策过程，就是从初始状态，到所有的都结束了，之间包含的所有transition。有点类似监督学习中的epoch。

1、状态转移的不确定性：

old state -> action -> new state

不确定行来源：

1. 执行动作的不确定性 $A->\pi (\cdot |S)$, 也即是说，小 a 是从函数中抽样出来的
2. 环境本身的也有随机性，下一状态也是随机抽样出来的。

2、状态行为轨迹 trajectory (state, action, reward)
$$s_1,a_1,r_1,s_2,a_2,r_2,\cdots ,s_T,a_T,r_t$$
3、Return (aka-> cumulative future reward)
$$U_t=R_t+R_{t+1}+R_{t+2}+R_{t+3}+\cdots$$

问题：$R_t$ 和 $R_{t+1}$ 在现在时刻看来一样重要吗

回答：不是一样重要，未来的 奖励， 在当前时刻应该加上相应的折扣，就像钱一样，未来的回报可能会贬值。所以我们需要在未来的奖励上都加上一些折扣，就衍生出下面的折扣汇报的概念。

4、Discounted return(cumulative discounted future reward)

discount rate：$\gamma$

折扣回报定义：
$$U_t=R_t+\gamma R_{t+1}+{\gamma }^2{R}_{t+2}+{\gamma }^3{R}_{t+3}+\cdots$$
从公式也可以看出来，当前时刻的回报也是一个随机变量，因为依赖与随机变量 动作 和 随机变量 环境。

​ 1、动作的随机性：$P[A=a|S=S]=\pi (a|s)$

​ 2、状态的随机性：$P[S^{‘}=s^{‘}|S=S，A=a]=p(s^{‘}|s，a)$

5、Action-value Function

因为上面的 回报 或者 折扣回报。我们在当前状态是都是不能直接获得其准确的值，我们只能计算其 大概的期望值，

定义：
$$\begin{gathered} Q_{\pi }(s_t,a_t)=\mathbb{E}[U_t|S_t=s_t,A_t=a_t] \\ s,t.U_{t}dependonaction{A}_t,A_{t+1},\cdots andstates{S}_t,S_{t+1},\cdots \end{gathered}$$
我们对所有的 t 时刻后面的 action 和 states 进行积分，会将 t 时刻之后的 action 和 states 积分掉，只剩下 t 时刻的 action 和 states，这样就形成了我们的 动作-价值函数 $Q_{\pi }$。此函数反应的为当前策略下，次行为和状态的 回报

6、 Optimal Action-value Function

因为行为函数 $\pi$ 会影响 行为价值函数，我们可以在 $\pi$ 的子集上面找出一个使得 KaTeX parse error: Undefined control sequence: \Q at position 1: \̲Q̲_\pi 函数最大化的结果，这个被称作最优化行为价值函数；

$$Q^{\ast }(s_t,a_t)=\underset{\pi }{\max }{Q}_{\pi }\left(s_t,a_t\right)$$

7、State-value function

是用来衡量当前 策略的好坏，因为对当前策略下的所有是动作所获得 回报 进行了平均化。
$$V_{\pi }(s_t)={\mathbb{E}}_A[Q_{\pi }(s_t,A)]$$
对于上面的 动作价值函数 和 状态价值函数，是被用来分别评价 当前 行为 和 当前 状态 的好坏；

动作价值函数：在给定策略函数 $\pi$, $Q_{\pi }(s_t,a_t)$是用来衡量根据当前状态选择当前行为的 好坏，因为我们选取的为平均值，估算这个行为之后的所有的行为均值作为评价函数，所以这个评价函数是评价当前行为之后获得总的好处；

状态价值函数：在给定所有的行为动作的选型之下，我们选取所有动作下的平均值来作为评价函数，这样就可以衡量当前状态的好坏。

两种学习方式

策略学习方式

函数形式：$\pi (a|s)$

第一步：给出观察到的状态 $s_t$

第二步：根据策略函数 $\pi$ ，随机选择 行为 $a_t$ , 也就是 随机采样：$a_t\sim \pi (\bullet |s_t)$

学习到一种各个行为在当前时刻的概率，再进行抽样。也就是没有给出各个行为的好坏，只是给出各个行为的概率。

在 Policy-based 算法中最著名的就是 Policy Gradient，而 Policy Gradient 算法又可以根据更新方式分为两大类：
1、MC 更新方法：Reinfoce 算法；
2、TD 更新方法：Actor-Critic 算法；

Reinfoce 算法是基于 MC 更新方式的 Policy Gradient 算法。MC 更新方式是指每完成一个 episode 才进行算法的更新，它是基于策略梯度的一种算法，策略梯度算法是指先找到一个评价指标，然后利用随机梯度上升的方法来更新参数使评价指标不断的上升。

Actor-Critic算法不是基于一个episode来进行更新的，完成一个 transition 就更新一下权值。

Reinfoce 和 Actor-Critic 使用神经网络去近似 策略函数 $\pi (a|s)$，如下图所示：

针对上面的拟合网络，我们输出的为各种动作的概率，但是我们没有真正的评价标准来对这一套概率进行误差的计算，因为我们没有真实值。所以我们需要 动作价值函数 $Q_{\pi }(s_t,a_t)$ 来对当前的 动作进行评价，再对所有的 动作的价值 进行平均化，就获得了当前策略的好坏。也即是使用 $V_{\pi }(s_t)={\mathbb{E}}_A[Q_{\pi }(s_t,A)]$，来进行衡量。

策略方法的梯度更新的具体流程:

我们并不知道 $Q_{\pi }(s_t,a_t)$，下面是两种解决解决方法：

Reinfoce

REINFORCE 的定义：使用 蒙塔卡罗 对 期望进行近似的方法，称作为 REINFORCE ；$V_{\pi }(s_t)={\mathbb{E}}_A[Q_{\pi }(s_t,A)]$，从现实场景中随机抽取应该 $a$，然后用 $Q_{\pi }(a)$ 的值来代表 $V_{\pi }(s_t)={\mathbb{E}}_A[Q_{\pi }(s_t,A)]$的值，被称作为REINFORCE ，

在 reinforce 的策略中，我们直接采用这一次 episode 后面的所有回报的和作为 $Q_{\pi }(s_t,a_t)$ 的近似。

公式如下：
$$\begin{gathered} \because \\ {Q}_{\pi }(s_t,a_t)=\mathbb{E}[U_t] \\ {u}_t=\sum _{k=t}^n{r}^{k-t}{r}^k \\ \therefore \\ {u}_t\approx Q_{\pi }(s_t,a_t) \end{gathered}$$
则误差 ${\delta }_t$ 公式如下：
$${\delta }_t=u_t-r_t-u_{t+1}$$
然后利用误差计算各个权值的偏微分，更新权重。

问题：$\lambda$ 的含义，$u_t$ 的含义, $r_t$ 的含义，

回答：$\lambda$是折扣汇报的比例， $u_t$ 是episode $U_t$ 的单次的实验的真实结果， $r_t$ 是执行完动作 $a_t$ 的回报。

Actor-Critic

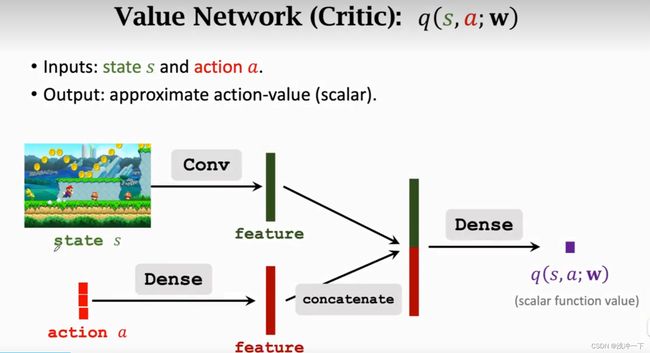
使用神经网络的方式来近似 动作价值函数，也就是使用 $q_t\approx Q_{\pi }(s_t,a_t)$ 对动作进行 “打分”。我们之前采用了 神经网络来近似 策略函数，加在一起就是两个神经网络，被称作为 actor-critic 的方法。

训练的时候当前时刻的奖励 $r_t$ 是已知的，且价值预测网络 Critic 输出的 $t$ 时刻的 动作价值为 $q_t$，但是 $t$ 时刻之后的奖励我们没有采用已经的奖励 $t_{t+1},\cdots ,t_n$，我们反倒将执行 $a_t$ 之后的下一时刻的状态 $s_{t+1}$ 输入我们的 价值预测网络 Critic 中，得到输出记作为 $q_{t+1} $，我们将误差记作 ${\delta }_t$，则
$${\delta }_t=q_t-(r_t+\lambda q_{t+1})$$
我们采用 ${\delta }_t$ 作为反向传播的误差，然后计算偏微分，更新各个权值。

问题：为什么是 $q_t$，而不是 $Q_t$ ，去近似 $Q_{\pi }(s_t,a_t)$

回答：其实符号的选择也是有含义的，$Q$ 代表是 $U$ (回报或者折扣回报) 的一种取均值的方式，但是我们网络这里仅仅是对其中的 一次 $U$来进行近似，其实也有一种进行 蒙特卡洛 近似 的含义。

多出来的 Critic Network 如下，和 Action 对state 的提取上可以公用一个 backbone，也可以将两个 backbone 分开。

3、下面训练这两个网络

大体上意图如下：

可以被分成下面几个步骤：

更详细的流程图如下：

最后一步使用 $q_t和{\delta }_t$ 都是可行的，$q_t$ 没有使用 baseline 的，${\delta }_t$ 使用了 baseline，后者减少了方差，会使得模型更容易收敛。

下面两个网络的梯度更新的方程式

价值学习方式

函数形式：$Q^{\ast }(s,a)$ 或则 $V_{\pi }(s_t)$ 或者 $Q_{\pi }(s_t,a_t)$ 都可以，采用不同的价值函数，将会被划分成不同的学习方法。

大体上步骤是相同，如下：

第一步：给出观察到的状态 $s_t$

第二步：从多个行为中选择一个行为最大化 行为价值函数，$a_t={argmax}_a{Q}^{\ast }(s,a)$

会给出明确的好的行为；没有给出行为的概率，只是给出各个行为的好坏。

两种学习方式的不同，

策略学习方式，是尽可能选择一个较好的策略，能够根据当前的状态给出下一个动作的分布概率，再从中抽样出动作，策略越好，应该好的行为被抽样的概率越大。(当前有且仅有一个策略， 和多个行为)，

而价值学习方式，是先从多个策略中找到利于当前状态的策略，再从所有的行为中，选取最好的行为。(包含多个策略和多个行为)

Q-learning和 DQN 算法都是强化学习中的 Value-based 的方法，它们都是先经过Q值来选择动作。下面将介绍这两种不同的网络：

价值学习Q-learning

使用已知的各个时间段的奖励 $r_1,r_2,\cdots ,r_n$ 来对 $Q^{\ast }(s_t,a_t)$ 进行蒙特卡洛近似的的方式被称为 Q-learning。再计算出误差 ${\delta }_t$ 的值进行对各个权值进行梯度更行，得到新的权值就行了。

公式如下：
$$\delta =q_t-r_t-q_{t+1}$$

价值学习 DQN

使用深度学习的方式来近似 最优的行为价值函数 $Q^{\ast }(s,a)$，因为现实场景下，我们不可能提前获得 最优的行为价值函数；

也就是在输入为 $S$，参数为 $W$， 输出为 $a$，的深度学习网络 $Q(s,a,;w)\sim Q^{\ast }(s,a)$

网络的大体框架如下：

网络的架构就 是单纯的卷积加上全连接层，如何输出各种行为动作的得分。

训练方式

TD算法

全称：Temporal Difference(TD) Learning

TD算法的核心是：

我们想知道某次动作之后，最终的结果，我们进行了预测，但是可能实践得到最终的结果的时间比较长，我们不能接受，假设当前从动作和结果之间我们还要分成好几小步，我们将第一小步的实际输出+ 后面几小步的预测输出 认为为最终的结果输出，和原本的预测结果做差，进行反向传播，这样做节约时间。也就是分批次进行反向梯度计算。

其实就是强化学习的一次过程可能需要很久，如果使用最终的结果作为一次反向传播，次数太少，耗时太久。采用每走一步进行一次计算，如何进行反向传播计算。

Multi-Step TD

和上面TD的更新方式类似，但是是对 TD 算法的一种优化。

只不过 不是每一个 transition 都更新一下梯度，而是进行了多个 transition，才更行一次参数。

公式如下：

那可能就会想了，要是使用后面的全部 transition，才更新一下梯度呢?

那就变成的 Reinfoce 了，不再是 Actor-Critic 方式了。

所以 Reinfoce 和 Actor-Critic 的差别：

在 梯度差值上，

REINFORCE： 使用已知的 后面的所有的奖励 $r_t\cdots$，等作为 critic 网络的预测，因为都是真实值，所以更高的可信度。

Actor-Critic： 仅仅使用当前 $r_t$ 的奖励真实值加上网络对 $t$ 时刻之后的奖励的值加在一起作为 critic 网络的预测。

就是说 Reinfoce 是 Actor-Critic 的一个特别的例子。

Alphago

MCTS

蒙特卡洛树搜索（简称 MCTS）是 Rémi Coulom 在 2006 年在它的围棋人机对战引擎 「Crazy Stone」中首次发明并使用的的 ，并且取得了很好的效果。
我们先讲讲它用的原始 MCTS 算法（ALphago 有部分改进）
蒙特卡洛树搜索，首先它肯定是棵搜索树

我们回想一下我们下棋时的思维——并没有在脑海里面把所有可能列出来，而是根据「棋感」在脑海里大致筛选出了几种「最可能」的走法，然后再想走了这几种走法之后对手「最可能」的走法，然后再想自己接下来「最可能」的走法。这其实就是 MCTS 算法的设计思路。

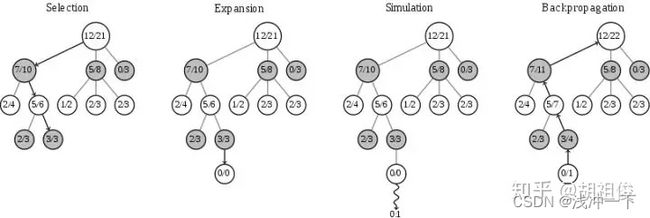
下面是蒙特卡洛树搜索的大致流程：（重复千千万万次）

1. 选择（Selection）
2. 扩展 (expansion)
3. 模拟（Simulation / Evaluation）
4. 回溯（Backpropagation）

选择（Selection）

就是在树中找到一个最好的值得探索的节点，一般策略是先选择未被探索的子节点，如果都探索过就选择UCB值最大的子节点。

我们将节点分成三类：

• 未访问：还没有评估过当前局面
• 未完全展开：被评估过至少一次，但是子节点（下一步的局面）没有被全部访问过，可以进一步扩展
• 完全展开：子节点被全部访问过
  我们找到目前认为「最有可能会走到的」一个未被评估的局面（双方都很聪明的情况下），并且选择它。

什么节点最有可能走到呢？最直观的想法是直接看节点的胜率（赢的次数/访问次数），哪个节点最大选择哪个，但是这样是不行的！因为如果一开始在某个节点进行模拟的时候，尽管这个节点不怎么好，但是一开始随机走子的时候赢了一盘，就会一直走这个节点了。
因此人们造了一个函数：
$$\mathbb{UCT}(v^{\prime },v)=\arg \underset{v^{\prime }\in childreofv}{\max }\frac{Q(v^{\prime })}{N(v^{\prime })}+C\sqrt{\frac{\log (N(v))}{N(v^{\prime })}}$$
其中 $v^{\prime }$ 代表当前节点， $v$代表当前节点的父节点，$Q(v)$ 是该节点赢的次数，$N(v)$ 是该节点模拟的次数，$C$ 是一个常数(可以控制exploitation和exploration权重)。

公式的解释：对每一个节点求一个值用于后面的选择。

前一部分的含义：是这个节点的平均收益值（越高表示这个节点期望收益好，越值得选择，用于exploitation）

后一部分的含义：右边的变量是这个父节点的总访问次数除以子节点的访问次数（如果子节点访问次数越少则值越大，越值得选择，用户exploration），因此使用这个公式是可以兼顾探索和利用的。

因此我们每次选择的过程如下——从根节点出发，遵循最大最小原则，每次选择己方 UCT 值最优的一个节点，向下搜索，直到找到一个「未完全展开的节点」，根据我们上面的定义，未完全展开的节点一定有未访问的子节点，随便选一个进行扩展。

扩展（expansion）

一般策略是随机自行一个操作并且这个操作不能与前面的子节点重复。将刚刚选择的节点加上一个统计信息为「0/0」的节点，然后进入下一步模拟（Simluation）

模拟（Simulation）

就是在前面新Expansion出来的节点开始模拟游戏，直到到达游戏结束状态，这样可以收到到这个expansion出来的节点的得分是多少。也就是需要在一个递归函数，直到尽头，然后返回每一个点的状态值，再进行选择新的点。直到完成全部完成。

回溯（Backpropagation）

Backpropagation 很多资料翻译成反向传播，不过我觉得其实极其类似于递归里的回溯，就是从子节点开始，沿着刚刚向下的路径往回走，沿途更新各个父节点的统计信息。

蒙特卡洛 近似方法

我们可以采用大数定律的方法来接近某一难以直接算出来的数值，比如$\pi$ 的真实值，我们取圆的半径为 1 ，将圆放入边长为 2 的正方形中，从 正方形 中随机取样点，总数记作 $n$，其中满足公式 $x^2 \ + \ y^2 < 1 $ 的个数记作 $m$，我们认为落在边界上的几乎不存在，我们认为边界线的宽度为 0。

这样，我们就可以计算出面积比：
$$\begin{gathered} \frac{\pi }{4}=\frac{m}{n} \\ 所以：\pi =\frac{4m}{n} \end{gathered}$$
根据大数定律，当 $n$ 足够大的话，上面的公式是满足的，这样我们就可以近似出 $\pi$ 的真实值。

上面是离散的情况下，当在连续的情况下的时候。我们先讨论最简单的一维度的情况下，$x\in [a,b]$，其中 x 为均匀分布。我们想要求 $f(x)$ 在 x 上的积分，公式如下：
$$I_{ab}={\int }_a^{b}f(x)dx$$
当 $f(x)$ 的原函数比较难求的情况下，即便是一个维度的积分，我们也是通过求原始函数来计算出 $I_{ab}$ 的值，我们可以采用和上面一样的大数近似的方法来求解。

第一步：计算出区间 $[a,b]$ 的 ”面积“，也就是 $S_{ab}={\int }_a^{b}1dx$ 。

第二步：任意在区间 $[a,b]$ 中采样 $n$个点，记作 $\{x_1,x_2,x_3,\cdots ,x_n\}$。并计算 $f(x_i)$的值，并计算其平均值$\overline{f(x_i)}$ ，使用其平均值来代表函数在 区间 $[a,b]$ 上的均值，当$n$足够大的时候，我们根据大数定律认为估计是准确的，按照两者均值来看，两者均值相同，可以认为是无偏估计。

第三步：使用均值来计算出 $I_{ab}$的结果。
$$\begin{gathered} I_{ab}=\overline{f(x_i)}\ast S_{ab} \\ 进一步 \\ {I}_{ab}={\int }_a^{b}1dx\ast \frac{1}{n}\sum _{i=1}^{n}f(x_i) \end{gathered}$$
从而我们便完成了对积分运算的近似计算。

上面的情况比较简单，我们通常面临的维度是复杂的，函数也是复杂，在积分的过程中，我们很难求出原函数，我们也可以采用上面近似的方式来计算。

设积分维度区域为 $\Omega$，积分函数记作为 $F(x)$，其他的掺杂函数为及作为$G(x)$。所求积分公式如下：
$$I_{\Omega }={\int }_{\Omega }F(x)\ast G(x)dx$$
步骤：

第一步：我们需要已知 ${\int }_{\Omega }G(x)dx$ 或者 ${\int }_{\Omega }dx$ 的结果，设结果为 $S_{\Omega }$ ;

第二步：在区域 $\Omega$ 上随机采样 $n$ 个数，记作 $\{x_1,x_2,x_3,\cdots ,x_n\}$，并计算其平均值 $\overline{f(x_i)}$ ，或则计算均值 $\overline{F(x_i)\ast G(x_i)}$。均值记作$A$。使用上面的均值来代表函数在区间 $\Omega$，上的均值。

第三步：使用均值来计算出 $I_{\Omega }$ 的值。
$$I_{\Omega }=S_{\Omega }\ast A$$
上述方法中将 $\int$ 符号变成 $\sum$ 符号也是同样的近似方法。

蒙特卡洛 近似方法：我们在现实场景下，我们难以选择大量的输出来近似 真实值，我们有的只是每一次的单一的真实值，这种情况下，我们认为单一的真实值就是 期望值 的近似。这种近似方法被称作为 蒙特卡洛近似。是期望值的无偏估计，因为算两者的均值是相同的。

Saras 算法

A2C and REINFORCE with baseline

Actor-Critic的定义：动作网络和之前一样，和上面不一样的是，我们不使用随机抽样来代表均值，我们使用神经网络来预测 $Q_{\pi }(a)$，这种方式被称作为 Actor-Critic。

在 REINFORCE 和 Actor-Critic 中加上 baseline 就变成了：

REINFORCE ==> REINFORCE with baseline

Actor-Critic ==> Advantage Actor-Critic (A2C)

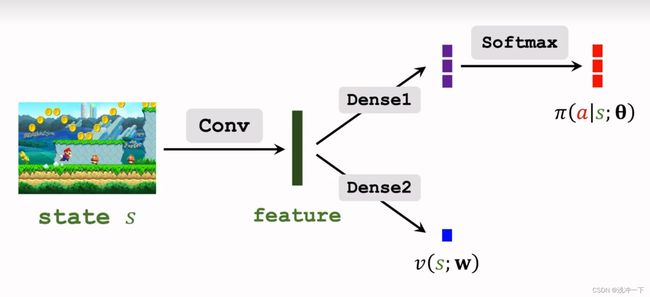
REINFORCE with baseline 和 Advantage Actor-Critic (A2C) 两者的网络架构图(是一样的)如下：

只不过 critic 网络的作用不同，在 REINFORCE with baseline 中，critic 输出的 $V(S;W)$，仅仅当作 baseline 减少 actor 网络中梯度的方差，但是在 A2C 中，critic 输出的 $V(S;W)$ ，是作为一种评价函数，直接评价 actor 的好坏。说白了一个预测这一次的动作的好坏，使用这一次的预测值评价，一个不使用这一次的评价函数，使用上一次的评价值和这一次的评价值的差值作为最终的评价值。

下面是 A2C 的主要流程：

看各种方法的差别，其实就是看 TD target 使用的目标函数 和 更新权值的时候使用的是否为 baseline 的差别。**

离散到连续空间

主要解决的方法如下：

直接离散的方式

我们在离散的强化学习中，所需要学习到的策略或者动作都是相对比较少的，我们使得网络能偶列举出所有的结果，但是在连续空间上，我们不能预测出一个连续的函数，也就是不能预测无穷多的解。

在维度输出维度比较少的情况下，我们可以采用将连续空间离散化的方法来进行解决，只考虑离散到的点，离散点之外的我们不进行考虑。但是在维度比较少的情况下，我们的离散点可能是比较少的，当维度增大的时候，离散的点随着维度的增加爆炸式的增长，我们的网络如果预测太多的输出，将使得网络的训练变得十分的困难，并且不显示。离散示意图如下：

确定策略梯度(DPG)

方法简介：

Deterministic Policy Gradient: 可以解决连续控制的问题

网络的架构如下：

确定性的来源：

策略网络的输出不再是一种概率分布，而是一个确切的值，这就是确切网络的来源。输入的维度是多少维度，那么我们的 action 就是多少维度的确切值，再使用 critic 网络对 action 网络的输出进行评价进行反向传既可。

价值网络的的权值更新:

按照上面的示意图，我们更新完成价值网络，我们就需要去更行 动作网络，动作网络的权值更新如下：

随机策略和确定策略

下面对比随机策略和确定策略的输入和输出的对比，

随机策略网络(SPN)

在面临连续控制的时候，如机械臂的控制，输出是机械臂的角度 $\Theta$ ，角度是一个连续的输出值，我们采用上面的确定值的输出的话，太多了，不可能完全对应上真值。这样我们上面的确定性网络就难以满足，我们需要一个满足连续输出的网络，但是如果一个网络输出太多的值的话，网络的训练将十分困难，并且不现实。

我们采用使得网络输出 均值 $\mu$ 和 标准差 $\sigma$ 。我们再从 均值 $\mu$ 和 标准差 $\sigma$ 中随机采样一个值，代替我们的确定性输出值，也解决了连续输出的问题。

当然这个均值和标准差所代表的 随机模型 是根据现实的要求来定的，可以是高斯模型，也可以是均值模型，等等。

若是采用高斯模型，也就是正太分布模型，如下：
$$\pi (a|s)=\frac{1}{\sqrt{2\pi }\sigma }.\exp (-\frac{(a-\mu {)}^2}{2{\sigma }^2})\sim \mathcal{N}(\mu ,{\sigma }^2)$$
连续策略概率函数就是我们带入 均值 $\mu$ 和 标准差 $\sigma$ 所求出来的正态分布概率密度函数。

在连续输入的维度是多个维度的情况下，在每一个维度上，我们都需要去预测出 均值 $\mu$ 和 标准差 $\sigma$ ，设输入的维度为 $n$，各个维度的均值 $\mu$ 和 标准差 $\sigma$ 分别记作 均值 ${\mu }_i$ 和 标准差 ${\sigma }_i$ 。则此时的 连续策略概率函数为：
$$\pi (a|s)=\prod _{i=1}^n\frac{1}{\sqrt{2\pi }{\sigma }_i}.\exp (-\frac{(a-{\mu }_i{)}^2}{2{\sigma }_i^2})\sim \mathcal{N}({\mu }_{new},{\sigma }_{new})$$
有多少维度， dense 输出的 均值 $\mu$ 和 标准差 $\sigma$ 就有多少维度，下面是输出为两个维度的情况。

下面是主要的网络架构如下：

其中 $\mu (s;{\Theta }^u)$ 是对 $\mu (s)$ 的近似， $\rho (s;{\Theta }^u)$ 是对 $\rho (s)$ 的近似，既然我们可以输出 均值 $\mu$ 和 标准差 $\sigma$ ，那网络网络的预测的输出为什么是均值 $\mu$ 和 $\rho$ 呢？为什么还会存在额外的输入 $Actiona$ 和一个输出层 $f(s,a;\Theta )$ 。

原因如下：

我们可以输出 均值 $\mu$ 和 标准差 $\sigma$ ，但是实践证明，标准差的范围比较大，难以训练，我们采用的输出为 方差的对数。也就是：
$$\rho =ln{\sigma }_i^2$$
从 $\rho$ 中，我们可以得到标准差 $\sigma$ ，也可以从其中采样得到相应的 $actiona\sim (a_1,a_2,\cdots ,a_n)$
$$a_i\sim \mathcal{N}(\widehat{{\mu }_i},\widehat{{\sigma }_i})foralli=1,\cdots ,n.$$
但是，输出来之后，该怎么评价呢？我们输出的 均值 $\mu$ 和 方差对数 $\rho$ 是不是满足我们的要求呢？方向传播的真实值该如何来呢？不额外添加的话，我们无法实现反向传播来优化我们的网络。

解决方法：在训练的时候，我们添加一个额外的输出的网络层 $f(s,a;\Theta )$ ，也就是构建一个额外的辅助神经网络 $f(s,a;\Theta )$。使用辅助神经网络 $f(s,a;\Theta )$ 对采样得到的 action 进行评价，也就是间接对 输出 均值 $\mu$ 和 方差对数 $\rho$ 进行评价， 来帮助 $Actor$ 网络进行训练。

方法步骤如下：

第一步：搭建辅助神经网络，$f(s,a;\Theta )$

我们想要求的 Policy 网络的 随机策略梯度为：
$$g(a)=\frac{\partial ln\pi (a|s,\Theta )}{\partial \Theta }.Q_{\pi }(s,a)$$
其中 $\frac{\partial ln\pi (a|s,\Theta )}{\partial \Theta }$ 为策略函数的梯度；

已知我们的策略网络公式如下：
$$\pi (a|s;{\Theta }^{\mu },{\Theta }^{\rho })=\pi (a|s)=\prod _{i=1}^n\frac{1}{\sqrt{2\pi }{\sigma }_i}.\exp (-\frac{(a-{\mu }_i{)}^2}{2{\sigma }_i^2})\sim \mathcal{N}({\mu }_{new},{\sigma }_{new})$$
我们可以从神经网络得出的 均值 $\mu$ 和 方差对数 $\rho$，得出近似的策略函数 $\pi$,我们也可以根据策略函数 $\pi$ 得到具体 action 的概率，但是一般情况下，我们不去计算策略函数 $\pi$，因为我们可以从 均值 $\mu$ 和 方差对数 $\rho$ 所代表的正太分布中直接抽取出相应的action。我们想要的只是 动作 action。

从策略提出函数 $g(a)$ 中我们不难发现，训练策略网络需要用到 $ln\pi (a|s,\Theta )$ ，我们将策略网络公式加上 $ln$进行变换如下：
$$\ln \pi (a|s;{\Theta }^{\mu },{\Theta }^{\rho })=\sum _{i=1}^n\left[-\ln {\sigma }_i-\frac{(a-{\mu }_i{)}^2}{2{\sigma }_i^2}\right]+const$$
其中 $const$ 代表变换之后的一些无关常数项。

又因为神经网络的输出是 方差对数 $\rho$，我们将 $\sigma^2 = \exp(\rho) $ 带入到上面的公式中，简化如下：
$$\ln \pi (a|s;\Theta )=\sum _{i=1}^n\left[-\frac{{\rho }_i}{2}-\frac{(a-{\mu }_i{)}^2}{2\exp ({\rho }_i)}\right]+const$$
其中：$\Theta =({\Theta }^{\mu },{\Theta }^{\rho })$

将
$$f(s,a;\Theta )=\sum _{i=1}^n\left[-\frac{{\rho }_i}{2}-\frac{(a-{\mu }_i{)}^2}{2\exp ({\rho }_i)}\right]$$
到这一步，我们的辅助神经网络 $f(s,a;\Theta )$ 就搭建好了，辅助神经网络的输出为 一个实数。可以看到，我们的辅助神经网络依赖当前时刻的 状态 $s_t$，当前时刻的 动作 $a_t$，还有 策略近似神经网络输出的 均值 $\mu$ 和 方差对数 $\rho$。

得到了当前的 $f(s,a;\Theta )$ 实数输出，我们就可以进行反向传播的梯度更新了.

更新流程如下：
$$\frac{\partial f(s,a;\Theta )}{\partial \Theta }->g(a)=\frac{\partial f(s,a;\Theta )}{\partial \Theta }.Q_{\pi }(s,a)$$
第二步：随机策略梯度下降

我们从上面可知：

随机策略梯度可转化为下面的形式：
$$g(a)=\frac{\partial f(s,a;\Theta )}{\partial \Theta }.Q_{\pi }(s,a)$$
其中：

$\frac{\partial f(s,a;\Theta )}{\partial \Theta }$ 的值可以直接算出来。就是一个函数求导。

$ Q_\pi(s, a)$ 是我们未知的变量，我们需要去近似。按照我们上面的认识，对 $ Q_\pi(s, a)$ 的近似有两种方式，分别是 Reinfoce 和 Actor-Critic。这里不在赘述。总之可以得到 $ Q_\pi(s, a)$ 的近似 $q_t$

然后使用下面的公式更新梯度即可：
$$\Theta <-\Theta +\beta \ast g(a)=\Theta +\beta \frac{\partial f(s,a;\Theta )}{\partial \Theta }.q_t$$
至次，策略网络的更新完成了。

多智能体强化学习

​ ==概述：==多智能体强化学习是在单体强化学习的基础之上，将多个单体联合起来，共同完成 或者 竞争完成 某一件事情，并将单体自身的利益最大化。

​ 注意：在不同的多智能体关系的情况下，单体自身利益最大化可能代表的含义和上面所介绍的单体的奖励有所不同。下面我们按照不同给关系，分析其中所获得 “利益最大化”

基本概念

1、完全合作关系

​ 概念：多个智能体之间需要共同完成某一件事，智能体之间完全没有竞争关系，智能体之间的利益是一致的， 只要完成了一致的目标，则所有智能体所获得的回报都是相同的。

​ 举例：多个机械臂合作搬东西，多个机器人合作将球踢入球门。

2、完全竞争关系

​ 概念：多个智能体之间没有共同目标，每个智能体都有自己的单一目标，竭尽全力的完成的自己的目标并同时不让对手的目标达成，在一次轮回当中，只有一个人的目标可以完成，也就是只能有一个智能体会获得奖励，其他智能体都不能获得奖励，典型为 0-1博弈，但有些竞争关系的双方的损失或者回报是不成比例的。

​ 举例：机器人拳击比赛。

3、合作和竞争关系的混合

​ 概念：多个智能体之间，某些智能体的关系是合作关系，某些智能体的关系是竞争，合作关系的智能体完成任务，则其中的每一个智能体都将获得相同的回报，与其相对应的是，另外一方为合作关系的智能体，则获得的不了任何奖励。

​ 举例：两队机器人进行足球比赛

4、利己主义

​ 概念：多个智能体存在的时候，还有一种关系叫做 “你是谁，关我毛事，我好就好了，你爱咋咋地”，就是智能体不会去和其他智能体有合作关系，也不会存在竞争关系，就是和其他智能体无关，它也不想损伤别的智能体的利益，也不想和其他智能体的利益一起最大化，只想要自己的本身的利益最大化。但是在现实场景下，完成自己本身的利益在一定程度上看到会损伤别人的利益或者促进别人的利益， 所以利己主义一般情况下，会造成竞争关系或者合作关系。

​ 举例：股市中的单个股民的操盘机器人，如马路全部都是无人车。

​

5、数学符号

1. 多智能体的数量：$n$
2. 当前的状态：$S$
3. 某一个 agent 的 action $A^i$
4. 状态转移公式：

$$p(s^{\prime }|s,a^1,\cdots ,a^n)=\mathbb{P}(S^{\prime }=s^{\prime }|S=s,A^1=a^1,\cdots ,A^n=a^n)$$

从上式可以看出，下一时刻的环境的状态依赖于当前所有 agent 的动作，这表明，每一个 agent 的动作都将影响到其他 agent 的动作，从而说明每一个 agent 都不是独立的。这将给训练带来很大的麻烦。

5. 每个 agent 的奖励 $R^i$
6. 第 i 个 agent 在时间 t 的回报 $U_t^i$

$$U_t^i=R_t^i+R_{t+1}^i+R_{t+2}^i+\cdots$$

7. 折扣回报 $U_t^i$

$$U_t^i=R_t^i+\gamma R_{t+1}^i+{\gamma }^2{R}_{t+2}^i+\cdots$$

8. 策略网络

9. 回报的不确定性

10. 状态价值函数

11. 纳什均衡

当其他的 单体 的策略不发生改变的发时候，另外其他一个 单体 的策略改变，将不会改变目前所有单体的状态，不会使得情况变得更好，这就是在多单体的情况下，评价多个单体策略函数均达到最优的办法。

12. 训练策略网络

如果单独的采用 单体 的训练网络的方式去训练 多体，将难以实现平衡，原因：

1、单体 策略网络的最大化中包含其他 单体的 参数

2、每个单体都在最大化自身的策略目标函数，且每个优化函数不相同，当其中的某一个好不容易达到最优的情况下，其他的 单体 优化自身改变了自身的参数，因为参数相互影响，则已经达到最优的 单体还要继续优化，永无止境。

一些概念

Bootstrapping

Bootstrapping 的解释图如下：也就是使用了自己本身不是很正确的参数去预测下一时刻的值进而更新自己的参数，就有点像“自踩”

Target Network

为了减少使用自己预测 的结果再反过来更新自己的参数，我们使用另外一个一模一样的网络来进行预测，再将预测的结果传递给现在的网络，但是另外一个网络的参数可能不会更新，或者很久更新一次，这种情况下，另外的网络就被称作为 Target Network。

Target Network 很久更新一次的策略也有很多种：Target Network权重为 $w_t$ ，原始的 actor 网络的多次更新之后的权重为 $w_a$

第一种的更新方式：$w_t$ = $w_a$ ；也就是直接赋值；

第二种的更新方式：$w_t=\alpha \ast w_a+(1-\alpha )\ast w_t$

举例如下：

1、更新价值网络，使用 Target Network 的方法

2、更新 动作网络，使用 Target Network 的方法

提升网络性能方法

1、Target Network：介绍如上

2、Experience replay：样本的被抽取的顺序不是固定的，也就是样本不是从头到尾开始的，我们对每一个样本计算相应的 “性能提升值”，扩展样本从 $(s_t,a_t,r_t,s_{t+1})->(s_t,a_t,r_t,s_{t+1}),{\delta }_t$，${\delta }_t$的值越大，代表样本约难，我们学习到的知识越多，这个样本在训练的过程中一个被抽取的次数更多，所以 ${\delta }_t$ 越大，其被抽取的概率应该更大，这就是经验重放的概念。

3、Multi-step TD Target：在每次更新的，我们并不仅仅使用当前的 $r_t$，可以使用 时间刻 $t$ 之后的连续的 $r_t,r_{t+1}$ 或 $r_t,r_{t+1}，r_{t+1}$ 或者 $r_t,r_{t+1}，r_{t+1}，\cdots$ ，这样更新的效果比单次更新的效果好，就相当于加上未来的动量在里面。

什么是 Baseline

Baseline设计思想基于以下的假设：

• 有些用户的评分普遍高于其他用户，有些用户的评分普遍低于其他用户。比如有些用户天生愿意给别人好评，心慈手软，比较好说话，而有的人就比较苛刻，总是评分不超过3分（5分满分）
• 一些物品的评分普遍高于其他物品，一些物品的评分普遍低于其他物品。比如一些物品一被生产便决定了它的地位，有的比较受人们欢迎，有的则被人嫌弃。

这个用户或物品普遍高于或低于平均值的差值，我们称为偏置(bias)

Baseline目标：

找出每个用户普遍高于或低于他人的偏置值$b_u$

找出每件物品普遍高于或低于其他物品的偏置值$b_i$

我们的目标也就转化为寻找最优的 $b_u$ 和 $b_i$（梯度下降求的就是这俩）

使用Baseline的算法思想预测评分的步骤如下：

• 计算所有电影的平均评分$\mu$（即全局平均评分）

• 计算每个用户评分与平均评分 $\mu$ 的偏置值$b_u$

• 计算每部电影所接受的评分与平均评分 $μ $ 的偏置值 $b_i$

• 预测用户对电影的评分：

$${\hat{r}}_{ui}=b_{ui}=\mu +b_u+b_i$$

举例：

比如我们想通过Baseline来预测用户A对电影“阿甘正传”的评分，那么首先计算出整个评分数据集的平均评分 $\mu$ 是3.5分；而用户A是一个比较苛刻的用户，他的评分比较严格，普遍比平均评分低0.5分，即用户A的偏置值 $b_u$ 是 - 0.5；而电影“阿甘正传”是一部比较热门而且备受好评的电影，它的评分普遍比平均评分要高1.2分，那么电影“阿甘正传”的偏置值 $b_i $ 是+1.2，因此就可以预测出用户A对电影“阿甘正传”的评分为：3.5 + ( − 0.5 ) + 1.2 3.5+(-0.5)+1.23.5+(−0.5)+1.2，也就是4.2分。

对于所有电影的平均评分$\mu$是直接能计算出的，因此问题在于要测出每个用户的 $b_u$ 值和每部电影的 $b_i$ 的值。对于线性回归问题，我们可以利用平方差构建损失函数如下：

$$\begin{gathered} Cost=\sum _{u,i\in R}(r_{ui}-{\hat{r}}_{ui}{)}^2 \\ =\sum _{u,i\in R}(r_{ui}-\mu -b_u-b_i{)}^2 \end{gathered}$$

加入L2正则化：
$$Cost=\sum _{u,i\in R}(r_{ui}-\mu -b_u-b_i{)}^2+\lambda \ast (\sum _u{b}_u^2+\sum _i{b}_i^2)$$

公式解析：

公式第一部分是用来寻找与已知评分数据拟合最好的 $b_u$ 和 $b_i$

公式第二部分是正则化项，用于避免过拟合现象