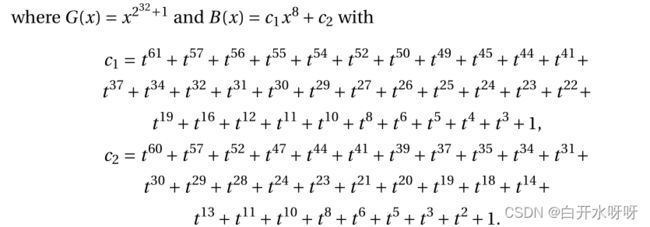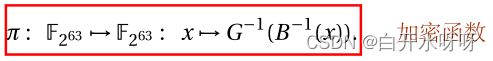读书笔记：Chaghri — an FHE-friendly Block Cipher

读书笔记：Chaghri — an FHE-friendly Block Cipher

---

---

摘要

算术复杂度是通过协议实现的电路中非线性操作的数量和布局来观察的。就这个度量进行优化的对称密钥算法称为代数密码。
在本文中，我们提出了CHAGHRI，一种FHE友好的分组密码，能够在bgv类方案中实现高效的密文转换。一个完整的CHAGHRI电路只需要16次乘法，32个Frobenius自同构和32个旋转就可以实现，所有这些都安排在一个深度-32的电路中。我们的HElib实现实现了0.26秒/位的吞吐量，比相同设置下的AES快65%。

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、引言

1.1研究背景

1.1.2分组密码

传统的分组密码由精心选择的线性和非线性层构建，以抵御经过充分研究的攻击。除了安全之外，传统的分组密码在硬件和软件实现上都很高效。根据目标应用程序域，它们会针对运行时间、门数或内存/功率消耗中的不同方面进行设计。例如，物联网设备需要更低的内存/功耗和门数，而高速路由器需要更低的延迟。当目标应用程序域是一个安全计算协议（多方计算(MPC)、零知识(ZK)证明和完全同态加密(FHE）时，需要考虑不同的效率度量。
算术化的意思：将计算转化为有限域上的代数运算序列

1.1.2 几种代数密码

随着高级加密协议的普及，出现了新的代数密码设计，如Mimc、Poseidon、Vision和Rescue。与传统的分组密码不同，为了提高使用它们的协议的效率，这些算法的设计是由算法复杂度驱动的，所以它们抵御的攻击也不同。
尽管针对ZK和MPC应用提出了许多代数密码，但在FHE环境下提出的代数密码并不多。FHE是一个有效的工具，可以消除阻碍数据共享的隐私障碍。
因此，设计一种对FHE友好的代数密码仍然是一个有待改进的研究领域。

1.1.3 本文贡献

本文贡献：
1.解决了加密带来的开销问题，提高了密码方案的效率
2.设计了一种对FHE友好的代数密码

二、背景知识

1.AES流程

AES加密分为四个步骤，分别是：字节替换、行移位、列混淆、轮密钥加

下以4*4矩阵为例

①字节替换
通过S盒完成一个字节到另一个字节的映射
②行移位
第一行保持不变，第二行左移一位，第三行左移2位，第4行左移三位

③列混淆

④轮密钥加
加密过程中，每轮的输入与轮密钥异或一次（当前分组和扩展密钥的一部分进行按位异或）；因为二进制数连续异或一个数结果是不变的，所以在解密时再异或上该轮的密钥即可恢复输入
##研究背景

设想场景
用户使用全同态加密对数据加密后外包给云服务器，会增加数据维度，增大通信开销；
如果使用分组加密对数据加密后再外包就不增加通信开销

2.marvellous策略设计代数密码

首先，marvellous策略由N轮迭代组成，每一轮分为两步，每一步包含三种操作：S盒变换、线性操作层、子密钥注入
第一轮的输入是一个明文和一个主密钥
①S盒变换
每一轮的输入状态是一个向量空间的元素q,它是一个素数或者2的指数幂，首先将这个素数经过一个S盒进行映射，g=x^α，后面可能还有一个可逆的仿射变换。（采用S盒是因为他的密码分析特性）
②线性操作层
目的：将局部属性扩散到整个状态中，提高分支数，从而提高安全性
操作：将状态向量乘以一个MDS矩阵，
③子密钥注入
来源：每一轮的子密钥都是由第一轮输入的主密钥使用key schedule并根据轮常数扩展而来
轮数
一个Marvellous轮的轮数被设定为2*max(r0,r1, 5)，其中r0被设定为可被差分和线性密码分析、高阶差分和插值攻击的最大轮数；r1被说成是可被Gröbner基础攻击的特定实例轮数。五是理智系数，用于保护密码不被多余的优化尝试所削弱。因此，任何Marvellous实例都被设定为至少有10轮。

vision

marvellous族中的一个函数
特别之处：
①状态域是2的指数幂
②S盒的变换函数是$$\theta 1:F2n\to F2n:x\to B(x-1)$$,
$$\theta 0:F2n\to F2n:x\to B^{-1}(x-1)$$.

rescue

也是marvellous族的一个函数
特别之处：
①状态域是素数p，而不是二的指数幂
②只包含一个幂函数映射，不包含仿射函数
找到一个和p-1互素的数α，然后构造变换函数
$$\theta 0:Fp\to Fp:x\to x^{1/\alpha }$$
$$\theta 1:Fp\to Fp:x\to x^{\alpha }$$

全同态加密FHE

FHE是一种先进的加密协议允许用户在加密数据上直接直接评估电路无需解密，然而FHE可能增加数据维度，极大增加通信开销，所以要利用FHE和对称加密的转码，同时实现加密状态下计算和降低通信开销

BGV 层级全同态

层级全同态加密的方案参数会限制其乘法深度，比普通全同态加密有更多限制
BGV反复采用模数切换使噪声一直保持在阈值之下，
参数相关： 密码文本c和秘钥s都为多项式环A上的向量，而明文空间是p≥2的$A^p$上的所有多项式，由循环多项式Φm（X）定义。此外，在同态评估过程中的任何一点，都有当前的整数模数q和当前的密匙s，它们随着同态操作的应用而变化
==解密：==通过对密码文本c和当前密匙s在Aq上的内积来完成的。然后，把结果还原为p的模数

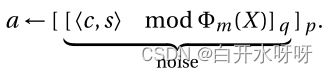
此外，密钥切换和模数切换知识用于电路评估，不会影响基础数据。
同态加法：通过向量加法实现，增加了密文的噪音，但不改变密钥和模数
同态乘法：通过向量内积实现，会造成密文为度增加从而改变了密钥，但不改变模数，大大增加了噪音
自同构：c是a在s和q下的密文，对c进行自动化操作，则其转化为的$c^{(i)}$即为$a^{(i)}$在$s^{(i)}$和q下的密文，不会增加密文噪音
密钥转换和模数转换：在增加密钥维度后进行密钥转换，模数转换的作用：减少密文噪音
打包密文：具体槽变换要根据自动化算法的情况，如果自动化中i是2的幂，则a转化为ai；否则就是不同槽之间的移位

非程序化计算

非程序化计算可以在运行中设定恒定运行时间，提高高级加密协议的效率
同时增加协议安全性，无需增加轮数

三、设计原理

CHAGHRI设计动机

对各种加密算法的性能进行了分析，决定分别进行改进和结合

性能比较

128位基准测试中：AES的性能比Vision快88%，比Rescue快96%。Vision和Rescue比AES慢的原因是它们需要更深的电路，而这些电路又需要更大的循环多项式Φ（m）来评估。因此，除了需要更多的原始操作（即乘法、加法和自动操作）外，由于Φ(m)较大，每个原始操作的运行时间也更长
更长尺寸测试：Vision增加状态元素的数量，它的吞吐量增加，同时保持延迟不变；而对于AES，吞吐量的增加迫使延迟线性增加。
这一比较分析的结论是，对于基场的较大扩展，反转和密集仿射多项式的计算是最昂贵的操作。即使Vision和Rescue在ZK和MPC中实现了紧凑的代数描述，它们在BGV中似乎表现不佳。这是因为Vision和Rescue都大量使用了ZK和MPC的特定非程序化操作
所以，vision和rescue在ZK和MPC中表现较好，因为可以被卸载到离线阶段，但是在FHE中表现不好，要考虑其他的方案

非程序化计算

因为上图操作的运行时间和指数无关，所以是一种非程序化计算，基本不增加噪音

仿射多项式

CHAGHRI采用稀疏化的仿射多项式

四、CHAGHRI

CHAGHRI是一个替换-互斥（SP）网络，它有一个组成的矢量状态，由三个场元素x0、x1、x2组成。一个CHAGHRI回合由两个相同的步骤组成。每个步骤有三层：S-box、线性和子密钥注入。
S-box层：对三个状态元素中的每一个场元素应用S-box π进行映射
线性层：将局部属性扩散到整体状态，S-box层的输出向量与大小为3×3的MDS矩阵M相乘
子密钥注入层：状态和相应的子密钥之间的XOR操作。

基本运算

黄金指数
在S盒中使用黄金指数，与反演相反，金指数独立于场扩展的梯度，它可以通过一个单独的Frobenius自同构计算。黄金指数的安全属性也已经被证明是高度非线性的，对微分和线性密码分析安全。然而，它们的低代数度构成了一个问题，我们通过使用精心选择的f2线性化仿射多项式，以与AES和Vision相同的方式缓解了这个问题。

由于实现黄金指数$x^{2^k+1}$的成本与k无关，我们希望最大化其安全效益。对于s = gcd(k,n)其中n是场扩展的度$x^{2^k+1}$是一个置换当且仅当n/s是奇数。此外，如果n是奇数和k的协素数，黄金指数是一个差分2-均匀排列，这可能会影响n的选择。n越大，对于固定数量的元素，吞吐量就会增加。由于n = 64不满足n/s为奇数，我们设n = 63和k = 32，结合f -线性化的仿射多项式提供了一个高多项式

S盒层
CHAGHRI中的S盒层，包含一个由仿射变换组成的指数映射函数$x^{\alpha }$

其中t是一个原始元素，c1 c2的选择后续说明。

轮数

λ是使用我们的方法可以被攻击的最大的轮数。然后，安全轮数由以下关系确定:N = 1.5 max(λ， 5)，其中常数5是marvelous设计师建议的健全系数，1.5是安全裕度。下表是使用不同方法可以攻击的轮数。

具体来说，1.5max(λ，5) = 7.5，然而，为了符合velvelous设计策略，我们取整并设N = 8为总轮数

解密函数

前文提到的都是客户端加密、服务器端解密同态计算，下文我们使用FHE友好的BGV解密，并使用它的逆描述加密算法。
CHAGHR使用8次轮函数，第一轮的输入是密文和主密钥，最后一轮输出是明文，而且第一轮之前和两轮之间以及最后一轮之后都要进行子密钥注入。

加密函数

先确定解密函数，然后根据解密函数的逆来确定加密函数

key schedule算法

为了生成子密钥注入环节要使用的子密钥，所以首先该算法要输入主密钥以及某些轮常量从而生成每一轮要注入的子密钥，注入轮常量可以抵抗某些攻击如旋转密码分析，循环常数注入后的中间状态作为子密钥提供。
轮常量的选择：不应该是循环不变量，也不能是q的场元素