从零开始机器学习：神经网络原理 + Python 简单实例

优秀外文博文搬运 + 翻译

原作者：Victor Zhou
链接：Machine Learning for Beginners: An Introduction to Neural Networks @Victor Zhou

本文为转载翻译内容，文章内容著作权归原作者所有

本文翻译已获得原作者授权

---

以下为翻译内容（斜体加粗部分为博主补充内容，非原文内容）：

在开始讲解之前有个惊喜给你：神经网络其实并不复杂！虽然“神经网络”这个词汇现在很流行并且听起来多么高大上，但事实上他们比人们想象中的要简单很多。

这篇博文是给那些几乎0基础的机器学习初学者准备的。我们将通过这篇文章理解神经网络的工作原理并且用 Python 从零开始实现一个。

让我们开始吧！

（虽说是 0基础教程，但不是什么都 0基础，博主还是建议有了解以下知识的朋友可以更好的理解这篇博文：

1. 基本高数：如线性代数，微积分等，当然数学部分其实也可以选择跳过；
2. 面向对象编程：因为原作者代码的编写方式是面向对象方法，了解 java 等类似编程语言的朋友更容易理解；）

1. 神经网络基本单元：神经元

首先，我们必须介绍一下神经元（neuron），也就是组成神经网络的基本单元。一个神经元可以接受一个或多个输入，对它们做一些数学运算，然后产生一个输出。下面是一个 2 输入的神经元模型：

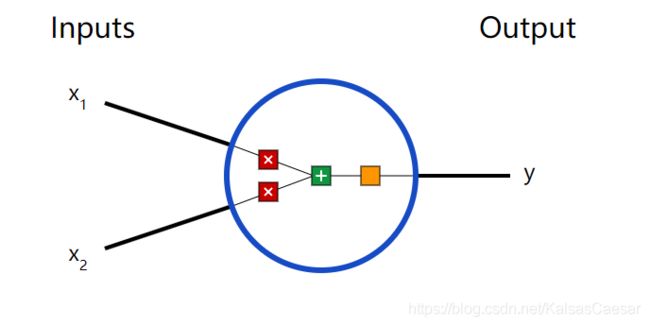
这个神经元中发生了三件事。首先，每个输入（$x_1$, $x_2$）会分别乘以一个权重值（weight）：
$$x_1\to x_1\ast w_1$$ $$x_2\to x_2\ast w_2$$

接下来，所有乘以了权重的输入将相加，并且再加上一个偏移量 $b$（bias）：
$$(x_1\ast w_1)+(x_2\ast w_2)+b$$

最后，这个最终相加的值还要再通过一个激活函数（activation function）：
$$y=f(x_1\ast w_1+x_2\ast w_2+b)$$

激活函数用来将那些无边界的输入转化成一组良好的，可预测的输出形式。一种常用的激活函数是 Sigmoid 函数：

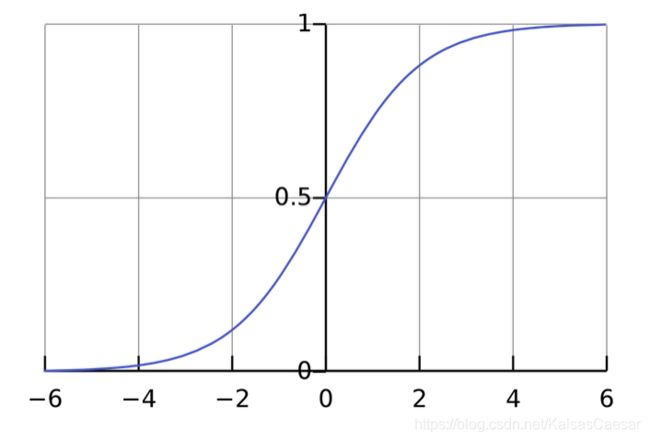
Sigmoid 函数仅输出 范围 (0, 1) 之间的数，你可以把它想象成将一组存在于 ($-\infty$, $+\infty$) 间的数字压缩到 (0, 1) 之间，越大的负数输出后会越接近 0，越大的正数输出后会越接近 1。

简单案例

假设我们有一个 2 输入且采用 sigmoid 激活函数的神经元，然后设置如下参数：
$$w=[0,1]$$ $$b=4$$

$w=[0,1]$ 是将 $w_1=0,w_2=1$ 写做向量的写法。现在，我们将给这个神经元一组输入 $x=[2,3]$。我们用点积（即 dot 运算，可以看做矩阵的乘法）的写法来更简洁的表达这个运算：

$$(w\cdot x)+b=((w_1\ast x_1)+(w_2\ast x_2))+b$$ $$=0\ast 2+1\ast 3+4$$ $$=7$$

$$y=f(w\cdot x+b)=f(7)=\boxed{0.999}$$

在给定输入 $x=[2,3]$ 的情况下，该神经元的输出是 $0.999$。 就是这样！这个将输入向前传递并且得到输出的过程称之为前馈（feedforward）。

编程实现一个神经元

是时候实现一个神经元了！这里我们会用到 NumPy 模块，这是 Python 中一种非常流行且功能强大的数据计算扩展程序库，它将帮助我们完成很多数学计算：

import numpy as np

def sigmoid(x):
  # 我们的激活函数: f(x) = 1 / (1 + e^(-x))
  return 1 / (1 + np.exp(-x))

class Neuron:
  def __init__(self, weights, bias):
    self.weights = weights
    self.bias = bias

  def feedforward(self, inputs):
    # 权重乘以输入，与偏移量相加，然后通过激活函数
    total = np.dot(self.weights, inputs) + self.bias
    return sigmoid(total)

weights = np.array([0, 1]) # w1 = 0, w2 = 1
bias = 4                   # b = 4
n = Neuron(weights, bias)

x = np.array([2, 3])       # x1 = 2, x2 = 3
print(n.feedforward(x))    # 0.9990889488055994

还记得这些数字吗？就是我们刚刚的例子里算出来的！我们在程序中得到了同样的结果 0.999。

2. 用神经元组合出一个神经网络

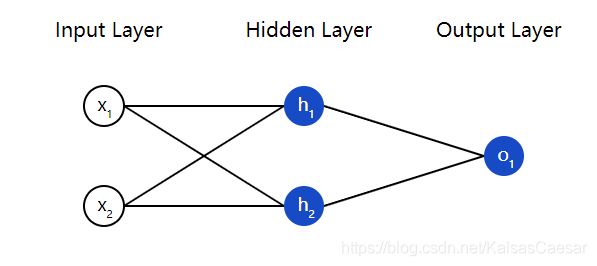
神经网络就是一群相互连接在一起的神经元，没别的东西。下面是一个简单的神经网络模型：

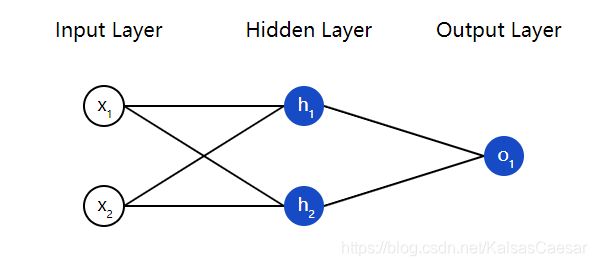
这个神经网络有 2 个输入（inputs），有一个 2 神经元（$h_1$ 和 $h_2$）的隐藏层（hidden layer），以及只有一个输出神经元（$o_1$）的输出层（output layer）。注意输出层 $o_1$ 的输入就是 $h_1$ 与 $h_2$ 的输出。这样几个简单的单元就构成了一个基础神经网络。

注：任何介于输入层（第一层）与输出层（最后一层）之间的层都叫隐藏层，隐藏层在神经网络中可以有多个（理论上不设上限 ）！

简单案例：前馈（Feedforward）

这个我们就以上面介绍的那个简单神经网络为例，并且假设每个神经元都有相同的权重 $w=[0,1]$，以及相同的偏移量 $b=0$，另外都采用 sigmoid 激活函数。令 $h_1$，$h_2$，$o_1$ 分别代表他们所对应神经元的输出。

准备完毕，那么如果我们放入一组输入 $x=[2,3]$ ，会发生什么呢？

$$h_1=h_2=f(w\cdot x+b)$$ $$=f((0\ast 2)+(1\ast 3)+0)$$ $$=f(3)$$ $$=0.9526$$

$$o_1=f(w\cdot [h_1,h_2]+b)$$ $$=f((0\ast h_1)+(1\ast h_2)+0)$$ $$=f(0.9526)$$ $$=\boxed{0.7216}$$

在输入为 $x=[2,3]$ 的情况下，该神经网络的输出为 $0.7216$。是不是很简单？

一个神经网络可以拥有任意数量的层，每个层也可以拥有任意数量的神经元。但是其运行的基础原理始终如一：将输入一层一层的向前喂给每一个神经元，并且最终得到输出（可以是一个输出，也可以是多个输出）。为了简单起见，我们还将继续用这个例子中的神经网络结构来介绍接下来的内容。

编程实现一个神经网络：前馈

我们来实现一个前馈网络，为了方便我们先把这个神经网络的结构图再放一遍：

import numpy as np

# ... code from previous section here

class OurNeuralNetwork:
  '''
  神经网络:
    - 2 个输入
    - 1 个隐藏层，2 个神经元 (h1, h2)
    - 1 个输出层，1 个神经元 (o1)
  所有神经元有同样的权重和偏移量:
    - w = [0, 1]
    - b = 0
  '''
  def __init__(self):
    weights = np.array([0, 1])
    bias = 0

    # 这里的 Neuron 类是上一节的代码里定义的
    self.h1 = Neuron(weights, bias)
    self.h2 = Neuron(weights, bias)
    self.o1 = Neuron(weights, bias)

  def feedforward(self, x):
    out_h1 = self.h1.feedforward(x)
    out_h2 = self.h2.feedforward(x)

    # o1 的输入就是 h1 和 h2 的输出
    out_o1 = self.o1.feedforward(np.array([out_h1, out_h2]))

    return out_o1

network = OurNeuralNetwork()
x = np.array([2, 3])
print(network.feedforward(x)) # 0.7216325609518421

我们最终又得到了 $0.7216$ ！看起来程序应该是没啥错。

3. 训练一个神经网络（一）

假如我们有如下数据：

姓名	体重（磅）	身高（英寸）	性别
Alice	133	65	女
Bob	160	72	男
Charlie	152	70	男
Diana	120	60	女

我们来用这些数据训练一个神经网络，让它能通过我们给出某人的身高和体重数据来预测这个人的性别：

我们用 0 来代表男性，用 1 来代表女性，并且我们需要将上面的数据转化一下以便使用：

姓名	体重（减135）	身高（减66）	性别
Alice	-2	-1	1
Bob	25	6	0
Charlie	17	4	0
Diana	-15	-6	1

注：我这里随意选了两个数字（135 和 66）来转化数据，让它们更好看更易处理。一般情况下应该用平均值对数据做相关处理（机器学习中一般训练数据前会对数据进行 标准化 / 归一化操作）。

损失（Loss）

（感觉“损失”放句子里怎么叫都别扭啊 >_<，下面直接用英文 loss 吧）

在训练神经网络之前，我们首先需要一种量化神经网络表现好坏的方法，这样才能让神经网络做得更好。这个量化的方法就是 loss（或者说损失函数）。

这里我们用均方误差（mean square error，注意和均方差区分开来）做为损失函数：

$$MSE=\frac{1}{n}\sum _{i=1}^n(y_{true}-y_{pred}{)}^2$$

让我们来解释一下这个公式：

• $n$ 是样本数，也就是 4 个（Alice, Bob, Charlie, Dinan）.
• $y$ 代表被预测量，也就是性别.
• $y_{true}$ 是被预测量 $y$ 的真实值（即所谓的“正确答案”）。比方说，Alice 的 $y_{true}$ 就是 1（女性）. （神经网络属于 “有监督的机器学习（supervised machine learning）”，在有监督的机器学习中，训练数据时需要给出每个样本的真实分类，供程序学习分析，也就是我们一般说的给数据 “打标签 ” 。很多时候， “打标签 ”这项工作是提前由人工手动完成的。神经网络算法将通过不断对比自己的输出与正确答案间的差距来优化自己，从而达到高精准度的预测能力。本文所讲解的 “损失函数 ”是神经网络对比差距的一种方法）
• $y_{pred}$ 代表预测后的结果值，也就是我们神经网络的最终输出.

$(y_{true}-y_{pred}{)}^2$ 是平方差。我们的损失函数就是简单的取所有平方差的平均值（所以叫均方误差）。如果预测结果越好，我们的 loss 也就越小！

更好的预测结果 = 更低的 loss 值

训练一个神经网络 = 试图将它的 loss 值降到最小

Loss 的计算案例

假设我们的神经网络训练后总是输出 0，换言之，它把所有的人都判别为男性。那么这种情况下这个神经网络的 loss 是多少呢？

姓名	$y_{true}$	$y_{pred}$	$(y_{true}-y_{pred}{)}^2$
Alice	1	0	1
Bob	0	0	0
Charlie	0	0	0
Diana	1	0	1

$$MSE=\frac{1}{4}(1+0+0+1)=\boxed{0.5}$$

编程实现：MSE Loss

计算 loss 的代码如下：

import numpy as np

def mse_loss(y_true, y_pred):
  # y_true 和 y_pred 是长度相同的 numpy 数组.
  return ((y_true - y_pred) ** 2).mean()

y_true = np.array([1, 0, 0, 1])
y_pred = np.array([0, 0, 0, 0])

print(mse_loss(y_true, y_pred)) # 0.5

好，又更进了一步！

4. 训练一个神经网络（二）

我们现在有了一个很清晰的目标，那就是将这个神经网络的 loss 努力降到最低。我们知道我们可以通过调整网络的权重值和偏移量来影响预测结果，但是具体要怎样操作才能减少 loss 呢？

这一节会用上一点儿多元微积分，如果你不太熟悉微积分，不用担心，完全可以跳过这一节。

为了简单起见，我们现在假设数据集中只有 Alice 这一个人的数据：

姓名	体重（减135）	身高（减66）	性别
Alice	-2	-1	1

这样的话，我们的均方误差就只是 Alice 数据的平方差：
$$L=MSE=\frac{1}{1}\sum _{i=1}^1(y_{true}-y_{pred}{)}^2$$ $$=(y_{true}-y_{pred}{)}^2$$ $$=(1-y_{pred}{)}^2$$

另一种分析 loss 的办法就是把 loss 看作一个与权重和偏移量相关的函数。我们先把神经网络中每个分支的权重和偏移量标到图上去：

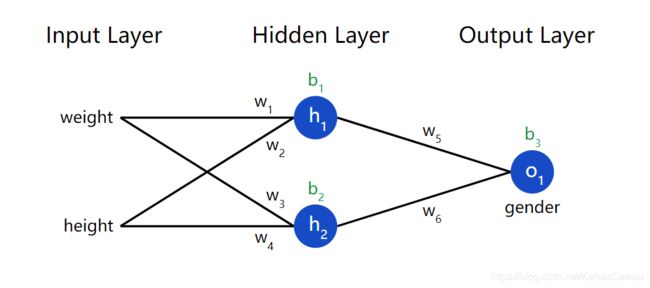
然后我们将 loss 写作一个多元函数：
$$L(w_1,w_2,w_3,w_4,w_5,w_6,b_1,b_2,b_3)$$

想象一下如果我们想调整 $w_1$ 的值，当我们改变 $w_1$ 的时候 $L$ 会如何变化呢？这个问题需要由偏微分（偏导数） $\frac{\partial L}{\partial w_1}$ 来解答。那如何来计算它呢？

从这里开始数学部分慢慢变得复杂了，但是别气馁！建议拿出纸笔跟着一起写写算算，这会帮助你理解。

首先我们将上述的偏微分重写成与 $\frac{\partial y_{pred}}{\partial w_1}$ 相关的形式（链式求导法则）：
$$\frac{\partial L}{\partial w_1}=\frac{\partial L}{\partial y_{pred}}\ast \frac{\partial y_{pred}}{\partial w_1}$$

由于我们之前算得了 $L=(1-y_{pred}{)}^2$，现在我们可以计算 $\frac{\partial L}{\partial y_{pred}}$ ：

$$\frac{\partial L}{\partial y_{pred}}=\frac{\partial (1-y_{pred}{)}^2}{\partial y_{pred}}=\boxed{-2(1-y_{pred})}$$

好，现在我们想想该怎么处理 $\frac{\partial y_{pred}}{\partial w_1}$ 。像之前那样，我们先令 $h_1,h_2,o_1$ 来分别代表每个神经元得输出。然后：
$$y_{pred}=o_1=f(w_5{h}_1+w_6{h}_2+b_3)$$
(这里得 $f$ 是 sigmoid 激活函数，还记得吗?)

由于 $w_1$ 只会影响 $h_1$ （不是 $h_2$），我们可以这样写：
$$\frac{\partial y_{pred}}{\partial w_1}=\frac{\partial y_{pred}}{\partial h_1}\ast \frac{\partial h_1}{\partial w_1}$$ $$\frac{\partial y_{pred}}{\partial h_1}=\boxed{w_5\ast f^{\prime }(w_5{h}_1+w_6{h}_2+b_3)}$$

然后我们对 $\frac{\partial h_1}{\partial w_1}$ 也做同样的操作：
$$h_1=f(w_1{x}_1+w_2{x}_2+b_1)$$ $$\frac{\partial h_1}{\partial w_1}=\boxed{x_1\ast f^{\prime }(w_1{x}_1+w_2{x}_2+b_1)}$$

$x_1$ 在这里是代表体重，$x_2$ 是身高。这是我们第二次看到 $f^{\prime }(x)$ （sigmoid 函数的导数）了，来求下导吧：
$$f(x)=\frac{1}{1+e^{-x}}$$ $$f^{\prime }(x)=\frac{e^{-x}}{(1+e^{-x}{)}^2}=f(x)\ast (1-f(x))$$

我们将在后面用这个非常耐斯的形式来代表 $f^{\prime }(x)$

我们做到惹！我们成功地将 $\frac{\partial L}{\partial w_1}$ 分解成了几个可以单独计算的部分：
$$\boxed{\frac{\partial L}{\partial w_1}=\frac{\partial L}{\partial y_{pred}}\ast \frac{\partial y_{pred}}{\partial h_1}\ast \frac{\partial h_1}{\partial w_1}}$$

这种通过逆向工作计算偏导数的方法被称作反向传播（backpropagation，简写 backprop）。

唔，写了不少难懂的符号。如果你还是有点困惑，没事儿，我们来个实际点的例子！

简单案例：计算偏导数

我们继续假设数据集里只有 Alice 一个人的数据：

姓名	体重（减135）	身高（减66）	性别
Alice	-2	-1	1

首先初始化定义这个神经网络所有的权重 $w$ 都为 1 并且所有的偏移量 $b$ 都是 0. 如果我们通过网络做前馈传递，将得到：
$$h_1=f(w_1{x}_1+w_2{x}_2+b_1)$$ $$=f(-2+-1+0)$$ $$=0.0474$$
$$h_2=f(w_3{x}_1+w_4{x}_2+b_2)=0.0474$$ $$o_1=f(w_5{h}_1+w_6{h}_2+b_3)$$ $$=f(0.0474+0.0474+0)$$ $$=0.524$$

神经网络的最终输出 $y_{pred}=0.524$，并不能很好的判别输入的身体数据属于男性（0）还是女性（1）。现在我们来计算下 $\frac{\partial L}{\partial w_1}$：

$$\frac{\partial L}{\partial w_1}=\frac{\partial L}{\partial y_{pred}}\ast \frac{\partial y_{pred}}{\partial h_1}\ast \frac{\partial h_1}{\partial w_1}$$ $$\frac{\partial L}{\partial y_{pred}}=-2(1-y_{pred})$$ $$=-2(1-0.524)$$ $$=-0.952$$

$$\frac{\partial y_{pred}}{\partial h_1}=w_5\ast f^{\prime }(w_5{h}_1+w_6{h}_2+b_3)$$ $$=1\ast f^{\prime }(0.0474+0.0474+0)$$ $$=f(0.0948)\ast (1-f(0.0948))$$ $$=0.249$$

$$\frac{\partial h_1}{\partial w_1}=x_1\ast f^{\prime }(w_1{x}_1+w_2{x}_2+b_1)$$ $$=-2\ast f^{\prime }(-2+-1+0)$$ $$=-2\ast f(-3)\ast (1-f(-3))$$ $$=-0.0904$$

$$\frac{\partial L}{\partial w_1}=-0.952\ast 0.249\ast -0.0904$$ $$=\boxed{0.0214}$$

提醒一下：我们之前对 sigmoid 激活函数求了导，即 $f^{\prime }(x)=f(x)\ast (1-f(x))$

我们做到啦！这个结果告诉我们如果增大 $w_1$，$L$ 将增长一点点点点。

训练神经网络：随机梯度下降法（SGD）

我们现在已经掌握了所有训练一个神经网络所需要的方法！ 接下来我们将使用一种叫做随机梯度下降（stochastic gradient descent，简写 SGD）的优化算法来告诉我们如何调整权重与偏移量的值以将 loss 最小化。它基础上是遵循这样一个更新方程：
$$w_1\leftarrow w_1-\eta \frac{\partial L}{\partial w_1}$$

$\eta$ 是被称作学习率（learning rate）的常量，它控制我们网络的训练速度。我们要做的其实就是用 $w_1$ 减去 $\eta \frac{\partial L}{\partial w_1}$：

• 如果 $\eta \frac{\partial L}{\partial w_1}$ 是一个正数，$w_1$ 会变小，进而让 $L$ 也变小
• 如果 $\eta \frac{\partial L}{\partial w_1}$ 是一个负数，$w_1$ 会变大，进而让 $L$ 还是变小

两种情况下均可以减小 loss。

如果我们对网络中的每一个权重和偏移量都用这种方法更新一遍，loss 就可以被慢慢减少，进而神经网络的表现就能得到提升。

我们的训练流程就会像下面这样：

1. 从数据集中选 1 个样本 —— 这也是SGD的特点，我们每次操作只用一个样本。
2. 计算 loss 对所有权重和偏移量的偏导数（比如：$\frac{\partial L}{\partial w_1}$，$\frac{\partial L}{\partial w_2}$，$\frac{\partial L}{\partial b_1}$ 等等）。
3. 使用更新方程去更新所有的权重和偏移量。
4. 回到第1步周而复始。

下面我们来实际操作一下！

编程实现：完整神经网络

终于到实现完整神经网络的时候了！！！：

姓名	体重（减135）	身高（减66）	性别
Alice	-2	-1	1
Bob	25	6	0
Charlie	17	4	0
Diana	-15	-6	1

import numpy as np

def sigmoid(x):
  # Sigmoid 激活函数: f(x) = 1 / (1 + e^(-x))
  return 1 / (1 + np.exp(-x))

def deriv_sigmoid(x):
  # Sigmoid 的导数: f'(x) = f(x) * (1 - f(x))
  fx = sigmoid(x)
  return fx * (1 - fx)

def mse_loss(y_true, y_pred):
  # y_true and y_pred 都是等长度的 numpy 数组.
  return ((y_true - y_pred) ** 2).mean()

class OurNeuralNetwork:
  '''
  神经网络:
    - 1 个隐藏层，2 个神经元 (h1, h2)
    - 1 个输出层，1 个神经元 (o1)

  *** 重要声明 ***:
  接下来的代码只是为了简单教学，没有任何方面的优化.
  真正的神经网络代码和这个完全不一样，千万别用这个代码当神经网络.
  相反，建议自己读一遍/跑一遍以更好地理解这个神经网络的工作原理
  '''
  def __init__(self):
    # 权重（weights）
    self.w1 = np.random.normal()
    self.w2 = np.random.normal()
    self.w3 = np.random.normal()
    self.w4 = np.random.normal()
    self.w5 = np.random.normal()
    self.w6 = np.random.normal()

    # 偏移量（biases）
    self.b1 = np.random.normal()
    self.b2 = np.random.normal()
    self.b3 = np.random.normal()

  def feedforward(self, x):
    # x 是有 2个元素的 numpy 数组.
    h1 = sigmoid(self.w1 * x[0] + self.w2 * x[1] + self.b1)
    h2 = sigmoid(self.w3 * x[0] + self.w4 * x[1] + self.b2)
    o1 = sigmoid(self.w5 * h1 + self.w6 * h2 + self.b3)
    return o1

  def train(self, data, all_y_trues):
    '''
    - 数据集是 (n x 2) 的 numpy 数组, n = 数据集中的样本数.
    - all_y_trues 是有 n 个元素的 numpy 数组.
      all_y_trues 中的元素与数据集一一对应.
    '''
    learn_rate = 0.1
    epochs = 1000 # 对整个数据集的训练总次数

    for epoch in range(epochs):
      for x, y_true in zip(data, all_y_trues):
        # --- 进行前馈操作 (我们后面要用到这些变量)
        sum_h1 = self.w1 * x[0] + self.w2 * x[1] + self.b1
        h1 = sigmoid(sum_h1)

        sum_h2 = self.w3 * x[0] + self.w4 * x[1] + self.b2
        h2 = sigmoid(sum_h2)

        sum_o1 = self.w5 * h1 + self.w6 * h2 + self.b3
        o1 = sigmoid(sum_o1)
        y_pred = o1

        # --- 计算偏导数.
        # --- 命名方式：d_L_d_w1 代表 "dL / dw1"，即 L对 w1求偏导
        d_L_d_ypred = -2 * (y_true - y_pred)

        # 神经元 o1
        d_ypred_d_w5 = h1 * deriv_sigmoid(sum_o1)
        d_ypred_d_w6 = h2 * deriv_sigmoid(sum_o1)
        d_ypred_d_b3 = deriv_sigmoid(sum_o1)

        d_ypred_d_h1 = self.w5 * deriv_sigmoid(sum_o1)
        d_ypred_d_h2 = self.w6 * deriv_sigmoid(sum_o1)

        # 神经元 h1
        d_h1_d_w1 = x[0] * deriv_sigmoid(sum_h1)
        d_h1_d_w2 = x[1] * deriv_sigmoid(sum_h1)
        d_h1_d_b1 = deriv_sigmoid(sum_h1)

        # 神经元 h2
        d_h2_d_w3 = x[0] * deriv_sigmoid(sum_h2)
        d_h2_d_w4 = x[1] * deriv_sigmoid(sum_h2)
        d_h2_d_b2 = deriv_sigmoid(sum_h2)

        # --- 更新权重（w）与偏移量（b）
        # 神经元 h1
        self.w1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w1
        self.w2 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w2
        self.b1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_b1

        # 神经元 h2
        self.w3 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w3
        self.w4 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w4
        self.b2 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_b2

        # 神经元 o1
        self.w5 -= learn_rate * d_L_d_ypred * d_ypred_d_w5
        self.w6 -= learn_rate * d_L_d_ypred * d_ypred_d_w6
        self.b3 -= learn_rate * d_L_d_ypred * d_ypred_d_b3

      # --- 在每10次迭代结束后计算总 loss并打印出来
      if epoch % 10 == 0:
        y_preds = np.apply_along_axis(self.feedforward, 1, data)
        loss = mse_loss(all_y_trues, y_preds)
        print("Epoch %d loss: %.3f" % (epoch, loss))

# 定义数据集 data
data = np.array([
  [-2, -1],  # Alice
  [25, 6],   # Bob
  [17, 4],   # Charlie
  [-15, -6], # Diana
])
all_y_trues = np.array([
  1, # Alice
  0, # Bob
  0, # Charlie
  1, # Diana
])

# 训练我们的神经网络!
network = OurNeuralNetwork()
network.train(data, all_y_trues)

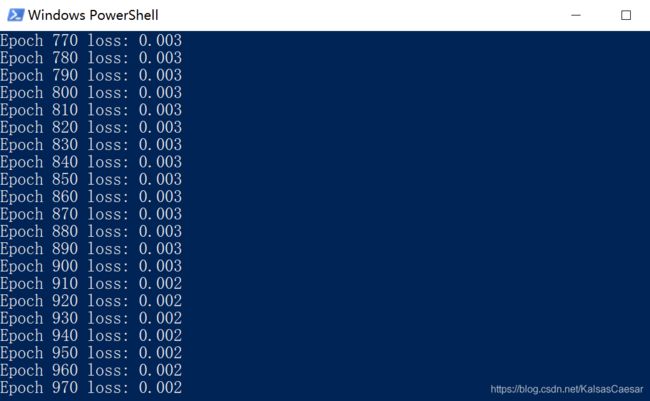
可以看到网络的 loss 值随着神经网络的自我学习而稳步下降：

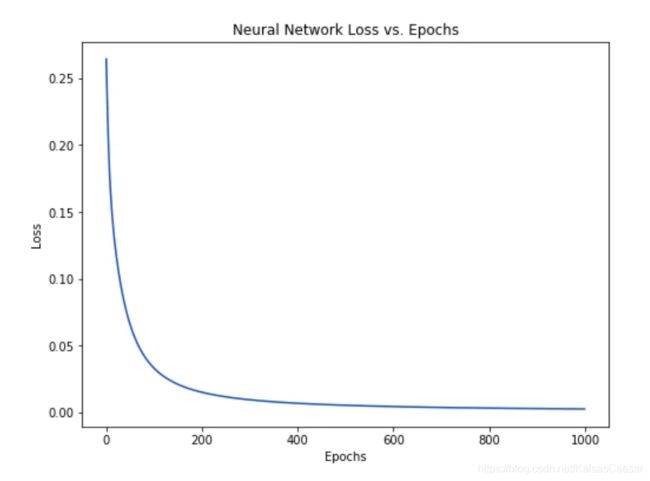
现在我们可以用这个神经网络来预测性别喽：

# 神经网络预测
emily = np.array([-7, -3]) # 128 磅, 63 英寸
frank = np.array([20, 2])  # 155 磅, 68 英寸
print("Emily: %.3f" % network.feedforward(emily)) # 0.951 - 女性
print("Frank: %.3f" % network.feedforward(frank)) # 0.039 - 男性

由于原作者没有放绘制 loss 图的代码，这里博主自己临时实现了一下：

首先需要引入绘图程序库 pyplot：

import matplotlib.pyplot as plt

之后我在 train 函数中临时定义了个空 list 来存储每次计算的 loss 数据，在每次计算 loss 那块 append一下，最后函数末尾返回这个 list：

def train(self, data, all_y_trues):
	lossdata = []  # 创建loss数据存放数组
	#.....函数主体省略......
	#..................
	if epoch % 10 == 0:
		y_preds = np.apply_along_axis(self.feedforward, 1, data)
		loss = mse_loss(all_y_trues, y_preds)
		lossdata.append(loss)  # 储存loss数据（每10次迭代）
		print("Epoch %d loss: %.3f" % (epoch, loss))

	return lossdata

最后在运行部分获取 loss 数据并绘图，横坐标是迭代次数（epoch），由于是每10次记录一次 loss 所以应该是100个点：

# 定义数据集
data = np.array([
  [-2, -1],  # Alice
  [25, 6],   # Bob
  [17, 4],   # Charlie
  [-15, -6], # Diana
])
all_y_trues = np.array([
  1, # Alice
  0, # Bob
  0, # Charlie
  1, # Diana
])

# 训练我们的神经网络!
network = OurNeuralNetwork()
lossdata = network.train(data, all_y_trues)  # 获取loss数据

fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.set_xlabel("epoch")  # 横坐标名
ax.set_ylabel("loss")  # 纵坐标名
ax.set_title("Neural Network Loss vs. Epochs")

epoch = range(0,1000,10) # 100个点
plt.plot(epoch,lossdata)  # 绘图
plt.show()

最后跑一遍，得到和原作者相近的结果：

写在最后

恭喜你坚持下来了！我们最后对本文内容做一个总结：

• 介绍了神经网络的基本单元——神经元。
• 在我们的神经元中采用了 sigmoid 激活函数。
• 发现神经网络就是一些连在一起的神经元而已。
• 创建了 身高 和 体重 的数据集作为输入（或叫特性 features），性别作为输出（或叫标签 label）。
• 学习了损失函数（loss functions）与均方误差（mean squared error）。
• 了解了训练一个神经网络就是最小化 loss 的过程。
• 用反向传播去计算偏微分。
• 用随机梯度下降法（SGD）来训练我们的神经网络。

恭喜，但是以后我们还有更多的路要走！