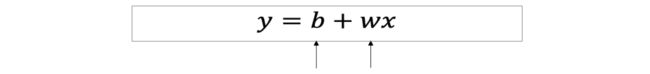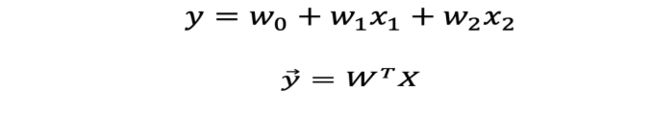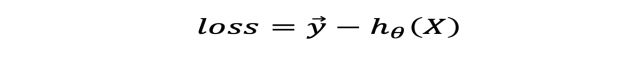TensorFlow 房价预测
以下资料来源于极客时间学习资料
• 房价预测模型介绍
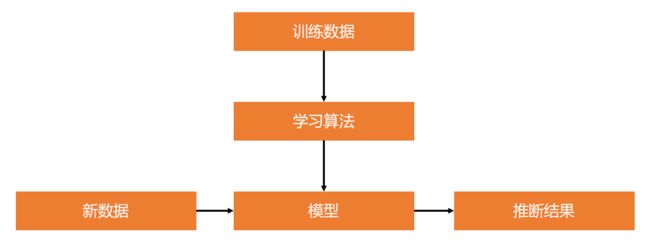
前置知识:监督学习(Supervised Learning)
监督学习是机器学习的一种方法,指从训练数据(输入和预期输出)中学到一个模型(函数),
并根据模型可以推断新实例的方法。
函数的输出通常为一个连续值(回归分析)或类别标签(分类)。
• 线性回归(Linear Regression)
• 逻辑回归(Logistic Regression)
• 决策树(Decision Tree)
• 随机森林(Random Forest)
• 最近邻算法(k-NN)
• 朴素贝叶斯(Naive Bayes)
• 支持向量机(SVM)
• 感知器(Perceptron)
• 深度神经网络(DNN)
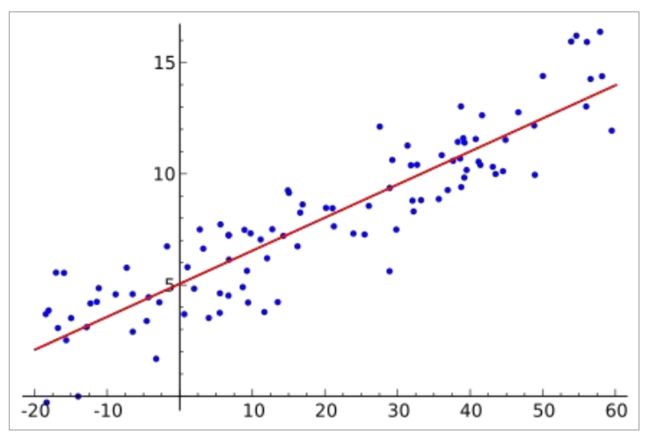
前置知识:线性回归
在统计学中,线性回归是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变
量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。
前置知识:单变量线性回归
理想函数:
梯度下降
多变量线性回归
理想函数
假设函数
梯度下降
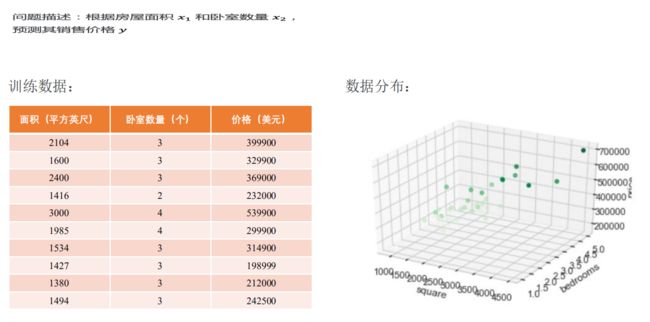
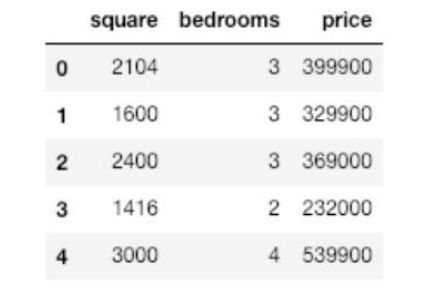
单变量房价预测问题
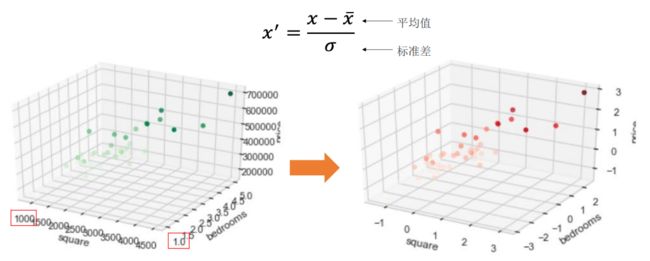
多变量房价预测问题:特征归一化
房屋面积和卧室数量这两个变量(特征)在数值上差了1000倍。在这种情况下,通常先进
行特征缩放(Scaling),再开始训练,可以加速模型收敛。
多变量房价预测问题
• 使用 TensorFlow 实现房价预测模型
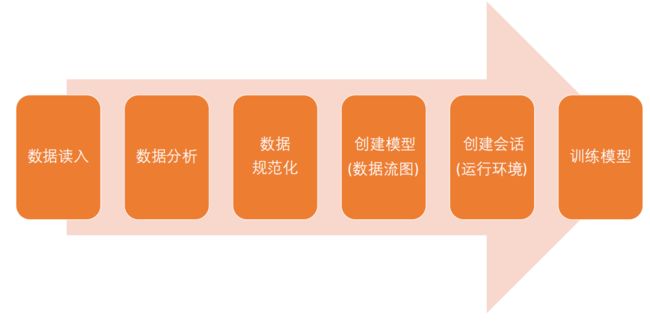
TensorFlow 训练模型的工作流
数据分析库:Pandas
Pandas 是一个 BSD 开源协议许可的,面向 Python 用户的高性能和易于上手的数
据结构化和数据分析工具。
数据框(Data Frame)是一个二维带标记的数据结构,每列(column)数据类型
可以不同。我们可以将其当作电子表格或数据库表。
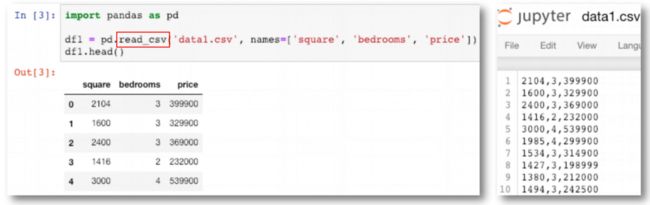
数据读入
pandas.read_csv 方法实现了快速读取 CSV(comma-separated) 文件到数据框的功能。
数据可视化库:matplotlib & seaborn & mplot3d
matplotlib 是一个 Python 2D 绘图库,可以生成出版物质量级别的图像和各种硬拷贝格式,
并广泛支持多种平台,如:Python 脚本,Python,IPython Shell 和 Jupyter Notebook。
seaborn 是一个基于 matplotlib的 Python 数据可视化库。它提供了更易用的高级接口,用
于绘制精美且信息丰富的统计图形。
mpl_toolkits.mplot3d 是一个基础 3D绘图(散点图、平面图、折线图等)工具集,也是
matplotlib 库的一部分。同时,它也支持轻量级的独立安装模式。
数据分析(2D)
seaborn.lmplot 方法专门用于线性关系的可视化,适用于回归模型。
数据分析(3D)
Axes3D.scatter3D 方法专门用于绘制3维的散点图。
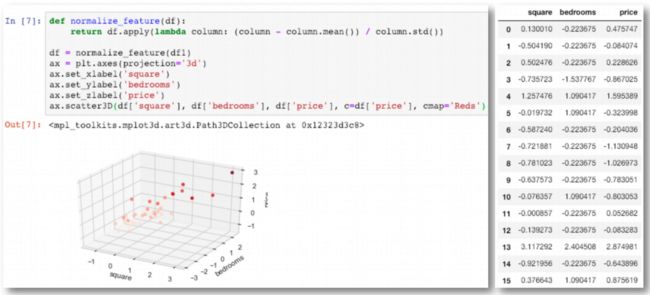
数据归一化(3D)
数据处理:NumPy
NumPy 是一个 BSD 开源协议许可的,面向 Python 用户的基础科学计算库,在多
维数组上实现了线性代数、傅立叶变换和其他丰富的函数运算。
测试代码:
单变量房价预测 import pandas as pd import seaborn as sns sns.set(context="notebook", style="whitegrid", palette="dark") df0 = pd.read_csv('data0.csv', names=['square', 'price']) sns.lmplot('square', 'price', df0, height=6, fit_reg=True)
df0.info() df0 '''RangeIndex: 47 entries, 0 to 46 Data columns (total 2 columns): square 47 non-null int64 price 47 non-null int64 dtypes: int64(2) memory usage: 832.0 bytes '''
多变量房价预测 import matplotlib.pyplot as plt from mpl_toolkits import mplot3d df1 = pd.read_csv('data1.csv', names=['square', 'bedrooms', 'price']) df1.head()
fig = plt.figure() # 创建一个 Axes3D object ax = plt.axes(projection='3d') # 设置 3 个坐标轴的名称 ax.set_xlabel('square') ax.set_ylabel('bedrooms') ax.set_zlabel('price') # 绘制 3D 散点图 # 通过字典的方式取 DataFrame 的列 # 参数 c 表示随着 price 值越大点的颜色越深,cmap即为颜色 ax.scatter3D(df1['square'], df1['bedrooms'], df1['price'], c=df1['price'], cmap='Greens')
数据规范化 def normalize_feature(df): return df.apply(lambda column: (column - column.mean()) / column.std()) df = normalize_feature(df1) df.head()
ax = plt.axes(projection='3d') ax.set_xlabel('square') ax.set_ylabel('bedrooms') ax.set_zlabel('price') ax.scatter3D(df['square'], df['bedrooms'], df['price'], c=df['price'], cmap='Reds')
df.info() '''RangeIndex: 47 entries, 0 to 46 Data columns (total 3 columns): square 47 non-null float64 bedrooms 47 non-null float64 price 47 non-null float64 dtypes: float64(3) memory usage: 1.2 KB ''' 数据处理:添加 ones 列(x0) import numpy as np ones = pd.DataFrame({'ones': np.ones(len(df))})# ones是n行1列的数据框,表示x0恒为1 ones.info() '''RangeIndex: 47 entries, 0 to 46 Data columns (total 1 columns): ones 47 non-null float64 dtypes: float64(1) memory usage: 456.0 bytes ''' df = pd.concat([ones, df], axis=1) # 根据列合并数据
df.head()
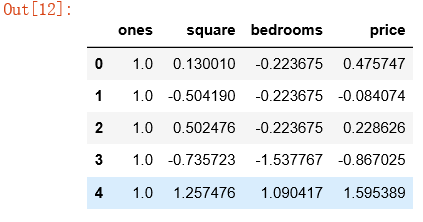
df.info() '''RangeIndex: 47 entries, 0 to 46 Data columns (total 4 columns): ones 47 non-null float64 square 47 non-null float64 bedrooms 47 non-null float64 price 47 non-null float64 dtypes: float64(4) memory usage: 1.5 KB '''
import pandas as pd import numpy as np def normalize_feature(df): return df.apply(lambda column: (column - column.mean()) / column.std()) df = normalize_feature(pd.read_csv('data1.csv', names=['square', 'bedrooms', 'price'])) ones = pd.DataFrame({'ones': np.ones(len(df))})# ones是n行1列的数据框,表示x0恒为1 df = pd.concat([ones, df], axis=1) # 根据列合并数据 df.head()
数据处理:获取 X 和 y X_data = np.array(df[df.columns[0:3]]) y_data = np.array(df[df.columns[-1]]).reshape(len(df), 1) print(X_data.shape, type(X_data)) print(y_data.shape, type(y_data)) ''' (47, 3)(47, 1) ''' 创建线性回归模型(数据流图) import tensorflow as tf alpha = 0.01 # 学习率 alpha epoch = 500 # 训练全量数据集的轮数 # 输入 X,形状[47, 3] X = tf.placeholder(tf.float32, X_data.shape) # 输出 y,形状[47, 1] y = tf.placeholder(tf.float32, y_data.shape) # 权重变量 W,形状[3,1] W = tf.get_variable("weights", (X_data.shape[1], 1), initializer=tf.constant_initializer()) # 假设函数 h(x) = w0*x0+w1*x1+w2*x2, 其中x0恒为1 # 推理值 y_pred 形状[47,1] y_pred = tf.matmul(X, W) # 损失函数采用最小二乘法,y_pred - y 是形如[47, 1]的向量。 # tf.matmul(a,b,transpose_a=True) 表示:矩阵a的转置乘矩阵b,即 [1,47] X [47,1] # 损失函数操作 loss loss_op = 1 / (2 * len(X_data)) * tf.matmul((y_pred - y), (y_pred - y), transpose_a=True) # 随机梯度下降优化器 opt opt = tf.train.GradientDescentOptimizer(learning_rate=alpha) # 单轮训练操作 train_op train_op = opt.minimize(loss_op) 创建会话(运行环境) with tf.Session() as sess: # 初始化全局变量 sess.run(tf.global_variables_initializer()) # 开始训练模型, # 因为训练集较小,所以每轮都使用全量数据训练 for e in range(1, epoch + 1): sess.run(train_op, feed_dict={X: X_data, y: y_data}) if e % 10 == 0: loss, w = sess.run([loss_op, W], feed_dict={X: X_data, y: y_data}) log_str = "Epoch %d \t Loss=%.4g \t Model: y = %.4gx1 + %.4gx2 + %.4g" print(log_str % (e, loss, w[1], w[2], w[0])) ''' Epoch 10 Loss=0.4116 Model: y = 0.0791x1 + 0.03948x2 + 3.353e-10 Epoch 20 Loss=0.353 Model: y = 0.1489x1 + 0.07135x2 + -5.588e-11 Epoch 30 Loss=0.3087 Model: y = 0.2107x1 + 0.09676x2 + 3.912e-10 Epoch 40 Loss=0.2748 Model: y = 0.2655x1 + 0.1167x2 + -1.863e-11 Epoch 50 Loss=0.2489 Model: y = 0.3142x1 + 0.1321x2 + 1.77e-10 Epoch 60 Loss=0.2288 Model: y = 0.3576x1 + 0.1436x2 + -4.47e-10 Epoch 70 Loss=0.2131 Model: y = 0.3965x1 + 0.1519x2 + -8.103e-10 Epoch 80 Loss=0.2007 Model: y = 0.4313x1 + 0.1574x2 + -6.985e-10 Epoch 90 Loss=0.1908 Model: y = 0.4626x1 + 0.1607x2 + -4.936e-10 Epoch 100 Loss=0.1828 Model: y = 0.4909x1 + 0.1621x2 + -6.147e-10 Epoch 110 Loss=0.1763 Model: y = 0.5165x1 + 0.162x2 + -7.87e-10 Epoch 120 Loss=0.1709 Model: y = 0.5397x1 + 0.1606x2 + -5.821e-10 Epoch 130 Loss=0.1664 Model: y = 0.5609x1 + 0.1581x2 + -9.08e-10 Epoch 140 Loss=0.1625 Model: y = 0.5802x1 + 0.1549x2 + -9.965e-10 Epoch 150 Loss=0.1592 Model: y = 0.5979x1 + 0.1509x2 + -9.756e-10 Epoch 160 Loss=0.1564 Model: y = 0.6142x1 + 0.1465x2 + -4.144e-10 Epoch 170 Loss=0.1539 Model: y = 0.6292x1 + 0.1416x2 + -1.001e-10 Epoch 180 Loss=0.1518 Model: y = 0.643x1 + 0.1364x2 + -3.236e-10 Epoch 190 Loss=0.1498 Model: y = 0.6559x1 + 0.131x2 + -6.286e-11 Epoch 200 Loss=0.1481 Model: y = 0.6678x1 + 0.1255x2 + 2.119e-10 Epoch 210 Loss=0.1466 Model: y = 0.6789x1 + 0.1199x2 + -1.956e-10 Epoch 220 Loss=0.1452 Model: y = 0.6892x1 + 0.1142x2 + -1.758e-10 Epoch 230 Loss=0.1439 Model: y = 0.6989x1 + 0.1085x2 + -4.307e-11 Epoch 240 Loss=0.1428 Model: y = 0.708x1 + 0.1029x2 + 3.376e-10 Epoch 250 Loss=0.1418 Model: y = 0.7165x1 + 0.09736x2 + 2.841e-10 Epoch 260 Loss=0.1408 Model: y = 0.7245x1 + 0.09189x2 + 3.295e-10 Epoch 270 Loss=0.14 Model: y = 0.732x1 + 0.08653x2 + -8.033e-11 Epoch 280 Loss=0.1392 Model: y = 0.7391x1 + 0.08128x2 + 1.141e-10 Epoch 290 Loss=0.1385 Model: y = 0.7458x1 + 0.07616x2 + 1.321e-10 Epoch 300 Loss=0.1378 Model: y = 0.7522x1 + 0.07118x2 + 5.087e-10 Epoch 310 Loss=0.1372 Model: y = 0.7582x1 + 0.06634x2 + 7.398e-10 Epoch 320 Loss=0.1367 Model: y = 0.7639x1 + 0.06165x2 + 6.845e-10 Epoch 330 Loss=0.1362 Model: y = 0.7693x1 + 0.0571x2 + 8.423e-10 Epoch 340 Loss=0.1357 Model: y = 0.7744x1 + 0.0527x2 + 9.252e-10 Epoch 350 Loss=0.1353 Model: y = 0.7793x1 + 0.04845x2 + 1.104e-09 Epoch 360 Loss=0.1349 Model: y = 0.784x1 + 0.04435x2 + 1.145e-09 Epoch 370 Loss=0.1346 Model: y = 0.7884x1 + 0.0404x2 + 1.631e-09 Epoch 380 Loss=0.1343 Model: y = 0.7926x1 + 0.03658x2 + 1.446e-09 Epoch 390 Loss=0.134 Model: y = 0.7966x1 + 0.03291x2 + 1.429e-09 Epoch 400 Loss=0.1337 Model: y = 0.8004x1 + 0.02938x2 + 1.694e-09 Epoch 410 Loss=0.1334 Model: y = 0.8041x1 + 0.02598x2 + 1.697e-09 Epoch 420 Loss=0.1332 Model: y = 0.8076x1 + 0.02271x2 + 2.125e-09 Epoch 430 Loss=0.133 Model: y = 0.8109x1 + 0.01957x2 + 2.292e-09 Epoch 440 Loss=0.1328 Model: y = 0.8141x1 + 0.01655x2 + 2.913e-09 Epoch 450 Loss=0.1326 Model: y = 0.8171x1 + 0.01366x2 + 3.412e-09 Epoch 460 Loss=0.1325 Model: y = 0.82x1 + 0.01087x2 + 3.749e-09 Epoch 470 Loss=0.1323 Model: y = 0.8228x1 + 0.008204x2 + 3.499e-09 Epoch 480 Loss=0.1322 Model: y = 0.8254x1 + 0.005641x2 + 3.663e-09 Epoch 490 Loss=0.1321 Model: y = 0.828x1 + 0.003183x2 + 4.2e-09 Epoch 500 Loss=0.132 Model: y = 0.8304x1 + 0.0008239x2 + 4.138e-09 '''
• 使用 TensorBoard 可视化模型数据流图
TensorBoard 可视化工具
在数据处理过程中,用户通常想要可视化地直观查看 数据集分布情况。
在模型设计过程中,用户往往需要分析和检查 数据流图是否正确实现。
在模型训练过程中,用户也常常需要关注 模型参数和 超参数变化趋势。
在模型测试过程中,用户也往往需要查看 准确率和 召回率等评估指标。
因此,TensorFlow 项目组开发了机器学习可视化工具 TensorBoard ,
它通过展示直观的图形,能够有效地辅助机器学习程序的开发者和使
用者理解算法模型及其工作流程,提升模型开发工作效率。
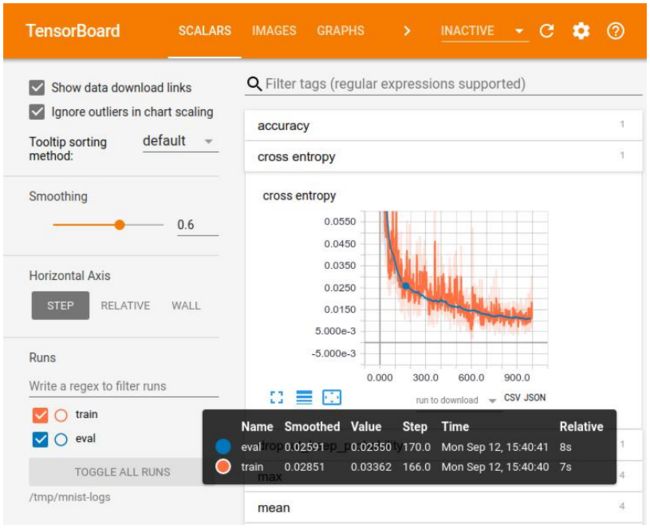
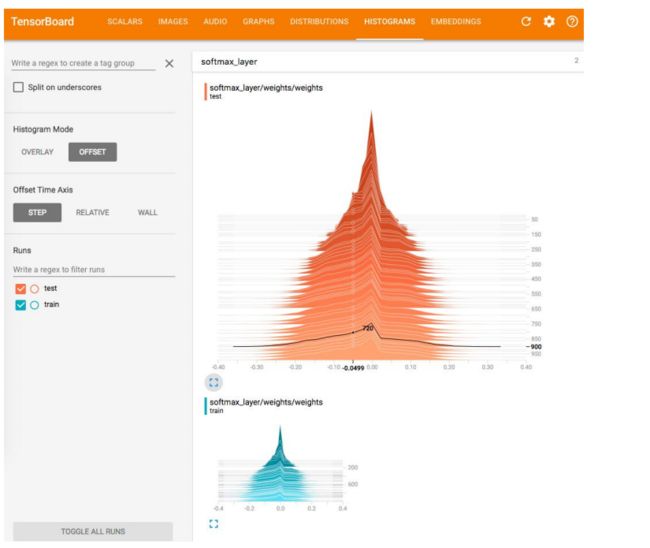
TensorBoard 可视化训练
TensorBoard 可视化统计数据
TensorBoard 可视化数据分布
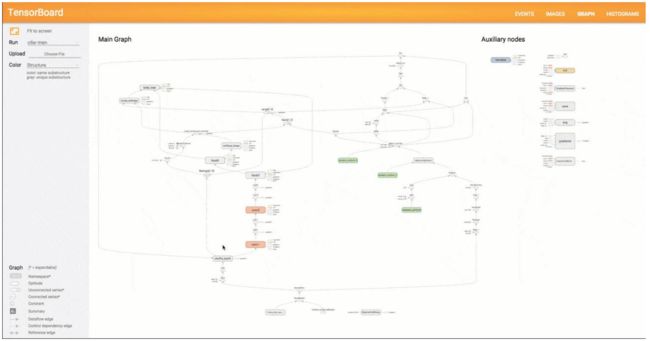
TensorBoard 可视化数据流图
TensorBoard 使用流程
可视化的数据是数据流图和张量,它们需要在会话中加载或执行操作后才能获取。然后,
用户需要使用 FileWriter 实例将这些数据写入事件文件。最后,启动 TensorBoard 程序,
加载事件文件中的序列化数据,从而可以在各个面板中展示对应的可视化对象。
tf.summary 模块介绍
前述流程中使用的 FileWriter 实例和汇总操作(Summary Ops)
均属于 tf.summary 模块。其主要功能是获取和输出模型相关的
序列化数据,它贯通 TensorBoard 的整个使用流程。
tf.summary 模块的核心部分由一组汇总操作以及
FileWriter、Summary 和 Event 3个类组成。
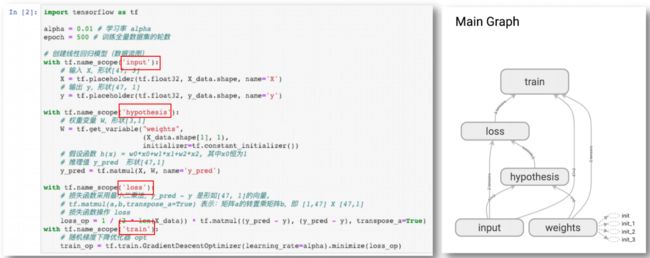
可视化数据流图 工作流
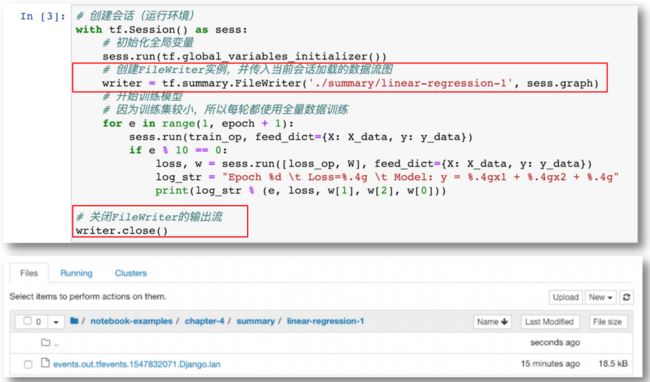
启动 TensorBoard
D:\Program Files\jupyter notebook\TensorFlow\TensorFlowTest\chapter-4\summary>tensorboard --logdir ./ --host localhost
测试代码:
import pandas as pd import numpy as np def normalize_feature(df): return df.apply(lambda column: (column - column.mean()) / column.std()) df = normalize_feature(pd.read_csv('data1.csv', names=['square', 'bedrooms', 'price'])) ones = pd.DataFrame({'ones': np.ones(len(df))})# ones是n行1列的数据框,表示x0恒为1 df = pd.concat([ones, df], axis=1) # 根据列合并数据 X_data = np.array(df[df.columns[0:3]]) y_data = np.array(df[df.columns[-1]]).reshape(len(df), 1) print(X_data.shape, type(X_data)) print(y_data.shape, type(y_data)) ''' (47, 3)(47, 1) ''' 创建线性回归模型(数据流图) import tensorflow as tf alpha = 0.01 # 学习率 alpha epoch = 500 # 训练全量数据集的轮数 with tf.name_scope('input'): # 输入 X,形状[47, 3] X = tf.placeholder(tf.float32, X_data.shape, name='X') # 输出 y,形状[47, 1] y = tf.placeholder(tf.float32, y_data.shape, name='y') with tf.name_scope('hypothesis'): # 权重变量 W,形状[3,1] W = tf.get_variable("weights", (X_data.shape[1], 1), initializer=tf.constant_initializer()) # 假设函数 h(x) = w0*x0+w1*x1+w2*x2, 其中x0恒为1 # 推理值 y_pred 形状[47,1] y_pred = tf.matmul(X, W, name='y_pred') with tf.name_scope('loss'): # 损失函数采用最小二乘法,y_pred - y 是形如[47, 1]的向量。 # tf.matmul(a,b,transpose_a=True) 表示:矩阵a的转置乘矩阵b,即 [1,47] X [47,1] # 损失函数操作 loss loss_op = 1 / (2 * len(X_data)) * tf.matmul((y_pred - y), (y_pred - y), transpose_a=True) with tf.name_scope('train'): # 随机梯度下降优化器 opt train_op = tf.train.GradientDescentOptimizer(learning_rate=alpha).minimize(loss_op) 创建会话(运行环境) with tf.Session() as sess: # 初始化全局变量 sess.run(tf.global_variables_initializer()) # 创建FileWriter实例,并传入当前会话加载的数据流图 writer = tf.summary.FileWriter('./summary/linear-regression-1', sess.graph) # 开始训练模型 # 因为训练集较小,所以每轮都使用全量数据训练 for e in range(1, epoch + 1): sess.run(train_op, feed_dict={X: X_data, y: y_data}) if e % 10 == 0: loss, w = sess.run([loss_op, W], feed_dict={X: X_data, y: y_data}) log_str = "Epoch %d \t Loss=%.4g \t Model: y = %.4gx1 + %.4gx2 + %.4g" print(log_str % (e, loss, w[1], w[2], w[0])) # 关闭FileWriter的输出流 writer.close() ''' Epoch 100 Loss=0.1835 Model: y = 0.4909x1 + 0.1621x2 + -6.147e-10 Epoch 200 Loss=0.1483 Model: y = 0.6678x1 + 0.1255x2 + 2.119e-10 Epoch 300 Loss=0.1379 Model: y = 0.7522x1 + 0.07118x2 + 5.087e-10 Epoch 400 Loss=0.1337 Model: y = 0.8004x1 + 0.02938x2 + 1.694e-09 Epoch 500 Loss=0.132 Model: y = 0.8304x1 + 0.0008239x2 + 4.138e-09 ''' 可视化损失值 print(len(loss_data)) ''' 500 ''' import matplotlib.pyplot as plt import seaborn as sns sns.set(context="notebook", style="whitegrid", palette="dark") ax = sns.lineplot(x='epoch', y='loss', data=pd.DataFrame({'loss': loss_data, 'epoch': np.arange(epoch)})) ax.set_xlabel('epoch') ax.set_ylabel('loss') plt.show()