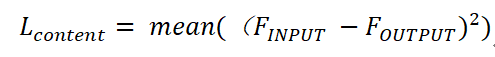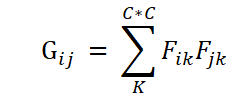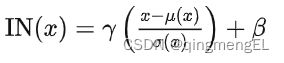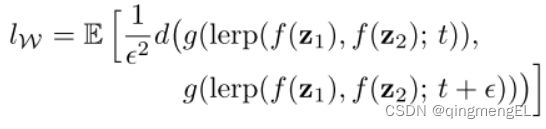StyleGAN 1~3学习

目录

StyleGAN1

潜在空间插值

风格迁移 

图像金字塔

随机噪声

插值算法

基于风格的生成器 

混合正则化

 特征向量解耦

感知路径长度

 线性可分性

截断技巧

---

StyleGAN1

潜在空间插值

        潜在空间即特征空间，在proGAN中的体现即为输入的噪声，如果生成器足够合理，则由一个噪声过渡到另一个的过程中，生成的图像也应当有过渡的体现。如：用第二个噪声的每一行依次替换第一个噪声中的对应行。

styleGAN1想解决的问题之一就是无法定量表示潜在空间插值的过程。（噪声无法实现“定量的过渡”）

styleGAN定量潜在空间插值的过程

风格迁移 

        风格迁移（Style Transfer），使用了两个损失函数，使得作为初始输入的随机噪声学习到内容图像（content）和风格图像（style）的特征，在过程中，使用到了两个损失函数：

内容损失函数

        

Gram矩阵

        Gram矩阵的大小为Chanel×Chanel。把特征图中第 i 层和第 j 层取出来，这样就得到了两个 WxH的矩阵，然后将这两个矩阵对应元素相乘然后求和就得到了 Gram(i, j)，同理 Gram 的所有元素都可以通过这个方式得到。这样 Gram 中每个元素都可以表示两层特征图的一种组合，换言之，它是特征通道的统计信息，代表着通道间的相关性。基于Gram矩阵得到下面的风格损失函数：

风格损失函数

        对两个损失函数加权相加（可控制学习趋向），即可得到总损失函数。

风格迁移架构

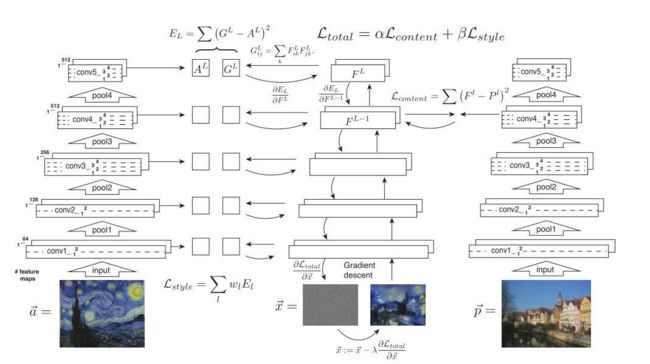
         先进行特征提取，在第四层求得内容损失；再进行上采样，在每一层均求风格损失并求和。

        然而上述风格迁移过程需要多次优化（在不同尺度上进行学习），耗时极长。在另一篇文章中提出了使用图像金字塔的方法提高模型的训练速度，这里又引入图像金字塔这一优化算法：

图像金字塔

        图像金字塔是由一幅图像的多个不同分辨率（尺度）的子图构成的图像集合，金字塔底部由大尺寸的原图组成，越往上层，尺寸越小，堆叠起来就是一个金字塔的形式。现在使用较为广泛的图像金字塔主要包含以下两种：

1. 高斯金字塔：将原图作为底层G0（C×H×W），使用5×5卷积核（高斯核）对其进行卷积，然后进行下采样，得到G1（C×H/2×W/2），以此类推，得到完整的金字塔。但问题在于经过高斯处理后的图像无法复原，原因在于在高斯卷积和下采样的过程中会损失部分信息。
2. 拉普拉斯金字塔：为了解决上面的问题，拉普拉斯金字塔中存储的就是上述损失的信息：Gk-1-upscale(Gk)，即低层减高层的上采样结果，将损失信息保存。这样就可以使用拉普拉斯金字塔对高斯金字塔进行修复。

高斯金字塔第四层与第一层的比较

将上图进行复原的结果

原图和经过修复的高斯金字塔

         图像金字塔可以赋予特征点尺度不变性，比如：在近处看到的目标会更清晰，远处反之，其实就是类似于将近处的目标的分辨率降低，也就是高斯金字塔中的更高层。如果在训练时就考虑到这点，对图像金字塔的每一层都进行特征提取后concatenate，那么在预测时也能不受图像尺度影响，精准预测特征点。

        原版的风格迁移模型在生成器的训练过程中实际上就是对每个尺度的特征都进行损失函数的求取，但是串行进行，而图像金字塔则是并行进行，极大程度上解决了实时性问题

        而后，使用图像金字塔的作者又通过将BN层修改为IN层，再次提高了收敛速度。IN层和BN层的区别在于：BN层对一个batch的数据进行归一化，而IN层仅对单个图像进行归一化。在其他训练任务中为了获得较高的泛化性，通常使用BN层来得到更加具有”包容性“的特征；而在风格迁移模型中，每张图片都可能有不同的风格，BN层无疑降低了风格的多样性，因此IN层更适用于风格迁移。而原作者在论文中的解释是：IN层实现了对比度的标准化，因而效果更好，但被AdaIN的作者通过实验否定了：

        另一作者又发现，修改其中的两个可训练参数，可达到潜在空间插值的效果。但每组参数仅对应一种风格：

         为了拓展风格数量，提出了AdaIN，其中参数换为了风格图像的均值和方差：

        再回到上面IN作者提出的对比度标准化问题，AdaIN做了如下实验：

         作者比较了输入图像为原始图像、对比度标准化后的图像以及风格归一化（均值方差归一化）后的分别使用BN层和IN层的模型损失。显然，对比度标准化并没有使二者的损失接近，而风格归一化做到了。这也使作者将两个放射参数修改为均值和方差的原因，但仍是实验得出的结论，还没有理论证明能够说明该结论。

随机噪声

        传统的生成器仅在输入层喂入输入，网络没办法在任何时候都可以对层的激活（即输出）加入对应的空间变化的伪随机数（不影响人脸内在特征的外部噪声），因为经过提取后的特征图在shape上和内容上都和初始的输入有所不同，这对算力要求极高而且伪随机数有周期性，这也是为什么传统的生成器会重复生成同一张图像。

        而本文中的生成器在每个尺度都加入噪声，防止仅对当前尺度下的风格造成影响（局部效应），且噪声由于对像素级产生随机影响，无法对样式（均值、方差等统计信息）造成宏观上（数据分布）的影响，而且如果噪声想要控制数据分布，也会被损失函数（使y和y`的数据分布近似）给限制。

插值算法

        第一种最简单的插值算法是最邻近插值插值算法，套用下面的公式即可，相当于坐标系的转换，但是一种简单的恒等映射关系，将目标图坐标进行缩放，反推源图坐标，得到的值四舍五入，把灰度值直接对应输入：

由原图像对应到目标图像

         上述方法使用四舍五入，把像素点强制确定了，但实际上得到的浮点数坐标不只受离它最近的像素点的影响，还受较远像素点的影响，比如：点（1.2，2.2）的像素值不应当被近似为（1，2）的像素值，还应受到其周围的（1，3）、（2，2）、（2，3）的影响，影响的比例就是浮点数的小数部分u、v、1-u、1-v：

 

基于风格的生成器 

        作者仅对生成器进行修改，鉴别器和损失函数仍沿用proGAN提供的，与其他学者这两部分的研究不矛盾 

基于风格的生成器架构

        现有的生成器架构直接将潜在码（latent code），即特征向量，作为初始输入，参与前向传播。这种情况下，潜在码必须满足训练数据的概率分布，则会导致不可避免地纠缠（entanglement），如：黑人毛发大多为短发，则潜在码在二者之间形成相关性，生成器仅生成短发黑人，无法生成长发黑人。因此作者首先将512维的潜在码先经过8层全连接层，将初始特征向量z映射到解纠缠的中间特征空间（W）。

        然后再通过仿射变换得到风格（均值和方差），作为AdaIN的两个参数。引入随机噪声以添加随机变异。

混合正则化

        作者在模型训练过程中使用两个潜在码z1、z2，对应着两个中间特征w1、w2，在训练的浅层、中层、深层分别使用z1/z2进行训练，而在其他层使用z2/z1，依次来说明不同层级改变的样式是不相关的。

 特征向量解耦

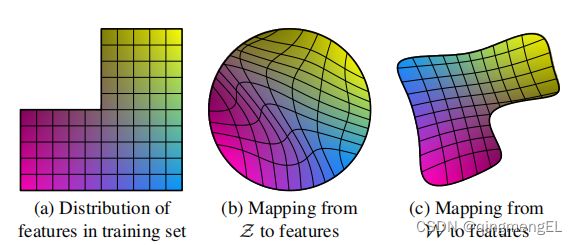
        现有的生成器架构直接将潜在码（latent code），即特征向量，作为初始输入，参与前向传播。这种情况下，潜在码必须满足训练数据的概率分布，则会导致不可避免地纠缠（entanglement），如：黑人毛发大多为短发，则潜在码在二者之间形成相关性，生成器仅生成短发黑人，无法生成长发黑人，此时的特征如图（a），会缺少“一块”特征：

         如果强制将该潜在码直接映射到特征空间，特征空间扭曲，空缺的部分被抹除掉，如图（b）；而映射网络就是防止在转换过程中特征空间扭曲，把“空白”保留下来给了该部分“空缺”得以“人工补全”的机会。

感知路径长度

        其他生成器将风格图像作为输入，使用编码器对特征编码，解耦程度的度量方式也都基于此类方法提出，但不适用于本文的架构。

        作者认为，如果解耦足够成功，那么潜在空间插值的过程应该是平滑的，不应当出现过渡突兀的点，因此可以将潜在空间的插值路径细分成小段，计算分段两端点间的”突兀程度“，求和，即为解耦是否成功的度量标准。

        是否突兀应当是通过人来判断，而现有的L2/PSNR/SSIM/FSIM等标准和人的判断并不相同：

两侧图片哪一个更接近中间的

         作者引入了感知距离（LPIPS），作为新的衡量标准：

         x为原图，x0为变形后的图，二者经过特征提取模型提取特征，然后在通道层次上归一化，使用w将输出缩放到余弦距离，逐个通道求L2距离，最后求取均值。

        PPL（感知路径长度）则是将每段的LPIPS相加，对整条路径求均值：

 线性可分性

        如果解耦足够成功，那么各个特征相互独立，两两之间可以通过超平面进行二分类。因此作者使用隐特征向量作为图像的标签，训练SVM，计算SVM和预训练的可信分类器的熵，熵小意味着SVM距离达到可信分类器的效果有多远。

截断技巧

        当图像的某一种分布在训练集中出现频率较低时，生成该类图像时图像质量不高。训练过程中求得w的均值（出现频率较高的特征），使得预测时的w向均值靠齐，增强图像质量，但降低了图像多样性。