PyTorch深度学习——梯度下降算法

目录

一、梯度下降算法（batch gradient descend）

二、随机梯度下降算法（stochastic gradient descend）

三、 小批量梯度下降算法（mini-batch gradient descend）

---

一、梯度下降算法（batch gradient descend）

原理：梯度下降算法是深度学习中很常见的一种方法，为了找到最优解，可以尝试利用穷举法，分治法或者贪心算法，梯度下降算法就是一种贪心的算法。通过不断的迭代，每次选取损失下降最快的方向去更新参数，可以很快达到局部最优解。如果函数是凸函数，局部最优解就是全局最优解；如果函数是非凸函数，可能会陷入局部最优解，或者神经网络中梯度为0的鞍点处，从而停止迭代。

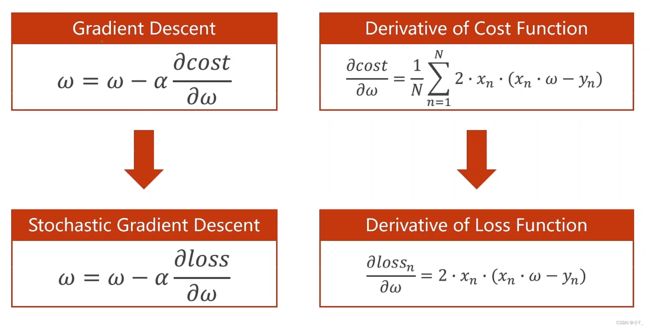
使用求导(Derivative)来获得梯度：

 w的更新公式：

 其中α是学习率，一般在开始训练前将其设置为learning_rate = 0.01。

代码

对线性目标函数的迭代更新过程：

import numpy as np
import matplotlib.pyplot as plt

#1.training set
x_data = [1.0,2.0,3.0,4.0]
y_data = [2.0,4.0,6.0,8.0]

#2.initial_w,initial_a
w = 1.0
a = 0.01

#3.functions
def forward(x):
    return x * w

def cost(xs, ys):
    cost = 0
    for x, y in zip(xs, ys):
        y_pred = forward(x)
        cost += (y_pred - y) ** 2
    return cost / len(xs)

def gradient(xs, ys):
    grad = 0
    for x, y in zip(xs, ys):
        grad += 2 * x * (forward(x)-y)
    return grad / len(xs)

#4.迭代100次
epoch_list = []
cost_list = []
#训练初始的预测值
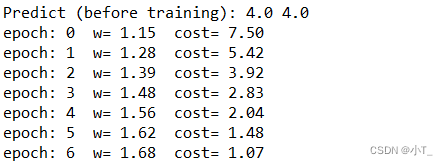
print('Predict (before training):',4.0,forward(4.0))
for epoch in range(100):
    cost_val = cost(x_data, y_data)
    grad_val = gradient(x_data, y_data)
    w -= a * grad_val
    print('epoch:', epoch, ' w=', '%.2f'%w, ' cost=', '%.2f'%cost_val)
    epoch_list.append(epoch)
    cost_list.append(cost_val)
#更新w后对y进行预测
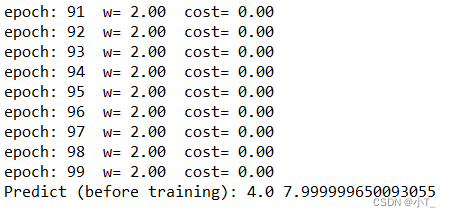
print('Predict (before training):', 4.0, forward(4.0))

#画图
plt.plot(epoch_list,cost_list)
plt.ylabel('cost')
plt.xlabel('epoch')
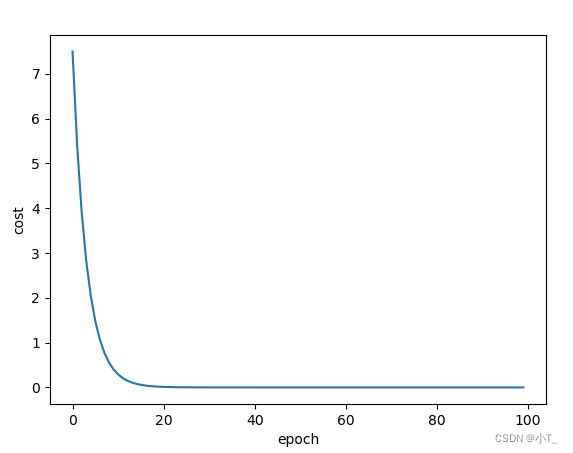
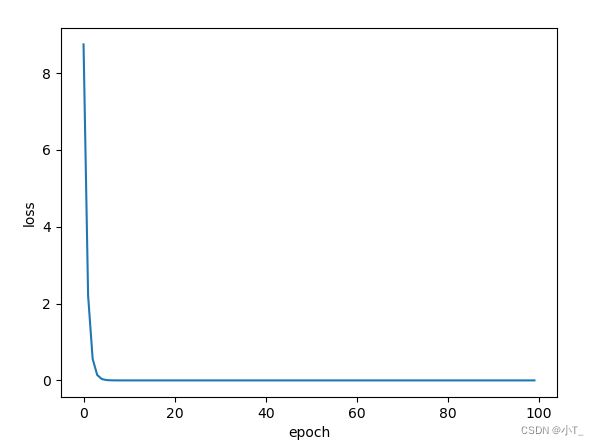
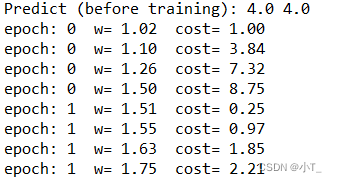
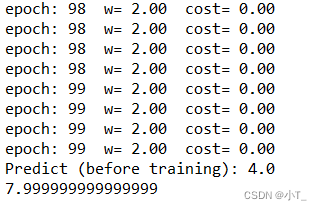
plt.show()

运行结果

经过100次的迭代后，权重更新到近似目标值2.0，预测值接近8.0。并且使用加权均值后的cost_function更加平滑。

---

二、随机梯度下降算法（stochastic gradient descend）

原理：不再使用全部样本的梯度均值来进行更新，而是在每一次的迭代中，从N个样本中随机抽取一个样本，利用单个样本的损失loss对权重w求导得到梯度，并对权重w进行更新。当遇到鞍点或者局部最小值时，随机的梯度有利于帮助跳出这块区域，使算法向最优点继续前进。

 代码

import numpy as np
import matplotlib.pyplot as plt

#1.training set
x_data = [1.0,2.0,3.0,4.0]
y_data = [2.0,4.0,6.0,8.0]

#2.initial_w,initial_a
w = 1.0
a = 0.01

#3.functions
def forward(x):
    return x * w

def loss(x, y):        
    y_pred = forward(x)
    loss = (y_pred - y) ** 2
    return loss

def gradient(x, y):
    return 2 * x * (forward(x)-y)


#4.迭代100次
epoch_list = []
loss_list = []
#训练初始的预测值
print('Predict (before training):',4.0,forward(4.0))
for epoch in range(100):
    for x, y in zip(x_data, y_data):
        loss_val = loss(x, y)
        grad_val = gradient(x, y)
        w -= a * grad_val
        print('epoch:', epoch, ' w=', '%.2f'%w, ' cost=', '%.2f'%loss_val)
        #选取每个数据进行更新w权重
    epoch_list.append(epoch)
    loss_list.append(loss_val)
#更新w后对y进行预测
print('Predict (before training):', 4.0, forward(4.0))

#plot
plt.plot(epoch_list,loss_list)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.show()
    

运行结果

梯度下降算法和随机梯度下降算法的区别是：

1、损失函数cost()更改为loss()，cost()计算的是全部数据的损失均值，而loss()计算的是单个数据的损失值。

2、梯度函数gradient()也从全部数据求出来的梯度均值变为单个数据所求的。

3、当epoch = 1时，即迭代100次，前者的w更新100次，而后者的w共更新100×4。

---

三、 小批量梯度下降算法（mini-batch gradient descend）

原理：将样本分成等量的子集，对每一个子集（mini-batch）做一次梯度下降并更新参数，这样可以在提高学习率的同时降低迭代次数。mini-batch的迭代成本函数是上下波动的，但总体呈下降趋势。

该算法需要创建Dataset和DataLoader对象，详情见下文链接。

---

三种算法的优缺点：

1、第一种梯度下降要遍历全部数据集之后才算一次损失函数，然后求各个参数的梯度并更新。这种方法的时间复杂度高且不支持在线学习。

2、第二种随机梯度下降是每次随机选取一个数据就要计算损失函数并更新参数，虽然更新迭代速度很快，但是收敛性能不好，因为可能存在噪声数据的影响，导致在最优点附近来回跳动，很难达到最优点。

3、为了中和上述两种算法的优缺点，采用小批量的梯度下降，把数据分成若干份，并对每一份进行参数更新。在一次参数更新中，是由一小批数据共同决定梯度方向，就避免了方向的巨大波动，能有效减少更新的随机性。