数字滤波器在语音信号处理中的应用及其设计方法

数字滤波器在语音信号处理中的应用及其设计方法
数字滤波器在语音信号处理中的应用较为广泛，主要有以下几个方面的应用：

1. 用于语音信号的减噪；
2. 用于基音频率的提取，使得基音频率落入（60~450HZ）之间；
3. 用于共振峰估计前的预加重处理，其中，预加重是让其通过一个一阶高通滤波器。

数字滤波器主要分为IIR和FIR两种，下面详细说明其设计方法及其设计流程。

IIR滤波器设计

IIR滤波器是由模拟滤波器的原型变换过来的，根据其滤波器传递函数的不同，可以将其分成4种，即巴特沃斯、切比雪夫I和切比雪夫II以及椭圆数字滤波器。
设计流程

1. 根据给定的参数（Wp,Ws,Rp,Rs）求出数字滤波器的阶数n和归一化的截止频率Wn（用0.5fs归一化）；
2. 由阶数n和截止频率Wn求取滤波器系数b和a；
3. 利用滤波器系数b和a，调用函数filter进行滤波处理。

4种滤波器对应的MATLAB函数及其调用方法如下所示：

%buttord
[n,Wn]=buttord(Wp,Ws,Rp,Rs);
[b,a]=butter(n,Wn,'ftype');
%cheb1ord
[n,Wn]=cheb1ord(Wp,Ws,Rp,Rs);
[b,a]=cheby1(n,Rp,Wn,'ftype');
%cheb2ord
[n,Wn]=cheb2ord(Wp,Ws,Rp,Rs);
[b,a]=cheby1(n,Rs,Wn,'ftype');
%ellipord
[n,Wn]=ellipord(Wp,Ws,Rp,Rs);
[b,a]=ellip(n,Rp,Rs,Wn,'ftype');

实例仿真
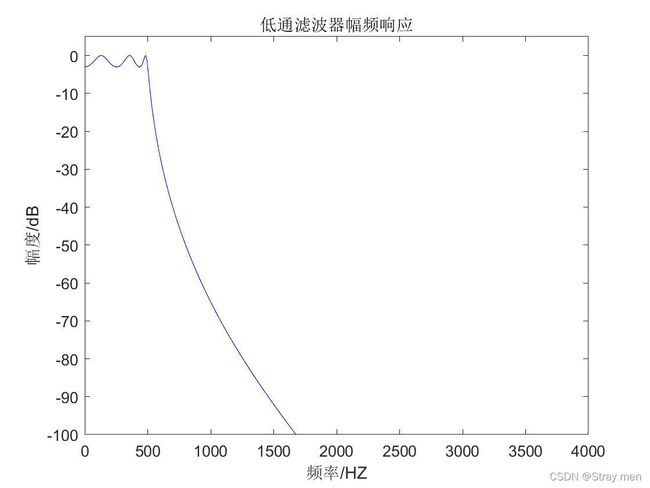
设计一个切比雪夫I型低通滤波器：通带截止频率fp=500,阻带截止频率fss=700,通带衰减Rp=3dB，阻带衰减Rs=40dB；语音信号和噪声都是正弦信号，语音信号频率fx=300,噪声信号频率fn=1000。利用低通滤波器消除噪声，其MATLAB代码如下：

%% IIR滤波器的设计——切比雪夫I型低通滤波器设计
%参数：通带截止频率fwp=500,阻带截止频率fws=700,通带衰减Rp=3dB，阻带衰减Rs=40dB
%语音信号和噪声信号考虑为正弦波信号，语音频率fx=300,噪声信号频率fn=1000
fs=8000;%采样频率
fs1=fs/2;
Fs=300;
Fn=1000;
t=(0:1:999)/fs;
y=sin(2*pi*Fs*t);%语音信号
noise=sin(2*pi*Fn*t);%噪声
Y=y+noise;%带噪信号
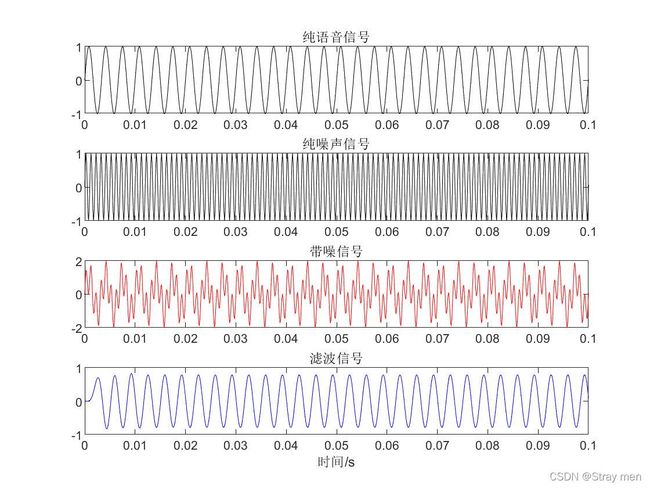
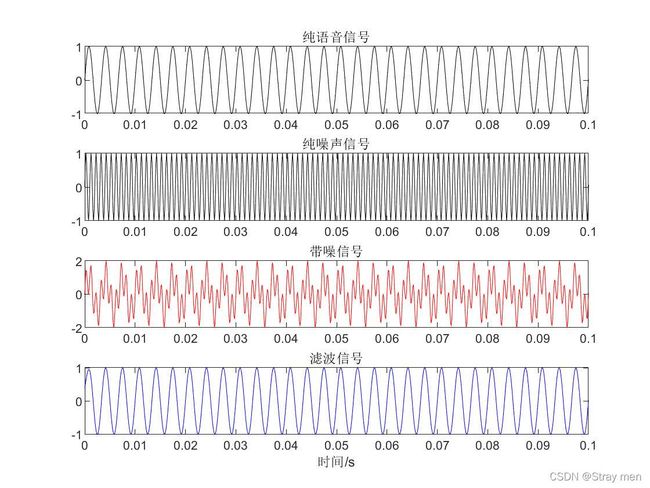
figure(1),subplot 411;plot(t,y,'k');xlim([0 0.1]);title('纯语音信号');
subplot 412;plot(t,noise,'k');xlim([0 0.1]);title('纯噪声信号');
subplot 413;plot(t,Y,'r');xlim([0 0.1]);title('带噪信号');

%设计IIR滤波器
Wp=500/fs1;%用0.5fs归一化
Ws=700/fs1;
Rp=3;
Rs=40;
[n,Wn]=cheb1ord(Wp,Ws,Rp,Rs);
[b,a]=cheby1(n,Rp,Wn);
[h,w]=freqz(b,a,4000);%计算频率响应
freq=w/pi*fs1;%频率刻度

figure(2),plot(freq,20*log10(abs(h)),'b');axis([0 4000 -100 5]);%dB输出
title('低通滤波器幅频响应');

%滤波处理
z=filter(b,a,Y);
figure(1),subplot 414;plot(t,z,'b');xlim([0 0.1]);title('滤波信号');

滤波结果

FIR滤波器设计

目前，FIR滤波器的设计方法主要是建立在对理想滤波器频率特性作某种近似的基础之上。主要的近似方法有窗函数法、频率抽样法和最佳一致逼近法。这里主要考虑窗函数法。窗函数法是利用给定的参数指标，通过查表来确定选用窗函数的类型，进而确定滤波器系数的过程。常用的几种窗函数特性表如下图所示。

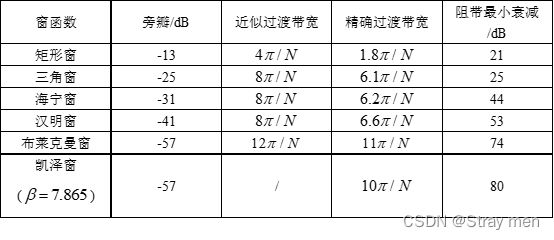
注意：
上图中的过渡带宽是利用采样频率fs进行归一化的带宽，而且对应着角频率2π。

设计流程

1. 根据阻带最小衰减Rs确定窗函数类型，窗函数的阻带最小衰减要大于所给定指标；
2. 根据过渡带宽小于给定带宽指标确定窗长N，窗长应该在满足指标的前提下越小越好；而且必须取奇数，因为其是偶对称的；
3. 计算窗函数Wd（直接调用函数）
4. 计算单位脉冲响应h(n)；
5. 进行滤波，输出结果，可以调用函数filter或者计算卷积conv。

注意：
这里提供两种利用窗函数Wd求得滤波器的单位脉冲响应h(n)的方法：
1.调用函数ideal_lp
其原理为利用理想低通滤波器去近似，从而得到现实中滤波器的单位脉冲响应h(n)，它是理想脉冲响应hd与窗函数Wn的乘积，在MATLAB中为点乘运算（.*）。对应的调用方式如下：

%理性低通
hd=ideal_lp(wc,M);
%理想高通
hd=ideal_lp(pi,M)-ideal_lp(wc,M);
%理想带通
hd=ideal_lp(wc2,M)-ideal_lp(wc1,M);%wc2>wc1
%理想带阻
hd=ideal_lp(wc1,M)+ideal_lp(pi,M)-ideal_lp(wc2,M);%wc2>wc1

注意：其中截止频率wc是归一化角频率（wc=fc*π/(0.5fs)），M为滤波器系数，取奇数，对应窗长N。
2.调用函数fir1
fir1是利用经典方法实现加窗线性相位FIR数字滤波器设计，其调用格式为，

H=fir1(n,Wn,'ftype',Window);
%n：阶数，等于N-1
%Wn：滤波器截止频率，用0.5fs归一化
%Window：窗函数Wd（窗长为N）即阶数与窗长之间相差1

实例仿真
和IIR一样设计低通滤波器，对1000HZ的噪声信号进行过滤处理。代码如下所示：

%% 设计FIR滤波器
fwp=500;Wp=fwp/fs1*pi;
fws=700;Ws=fws/fs1*pi;
Wc=(Wp+Ws)/2;%截止频率
Rs=40;%根据表格选择阻带衰减大于Rs=40的窗
df=(fws-fwp)/fs;%过渡带宽（用采样频率fs归一化），再根据表格要使得窗长N最小，则应该选择布莱特曼窗
%本程序为了说明流程，选择汉明窗
N=6.6*pi/(2*pi*df);%汉明窗的过渡带宽计算公式
N=N+mod(N+1,2);%窗长为奇数
M=N-1;%阶次
Wd=hamming(N);%窗函数
%计算滤波器的单位脉冲响应
% %% 用理想低通滤波器逼近
% hd=ideal_lp(Wc,N);
% b=hd.*Wd';

% 用firl函数设计
b=fir1(M,Wc/pi,Wd);%用0.5fs归一化（不带pi）

[h,w]=freqz(b,1,4000);
freq=w/pi*fs1;%频率刻度

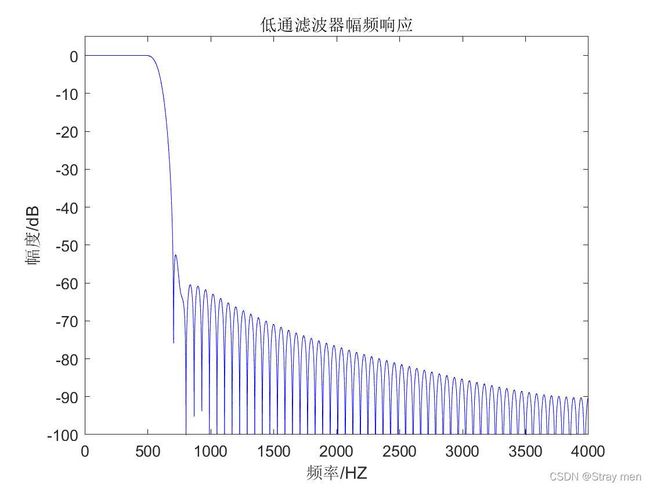
figure(2),plot(freq,20*log10(abs(h)),'b');axis([0 4000 -100 5]);
title('低通滤波器幅频响应');
xlabel('频率/HZ');ylabel('幅度/dB');

z=filter(b,1,Y);
% z=conv(b,Y);%求卷积的方式求解
figure(1),subplot 414;plot(t(1:end-M),z(fix(M/2)+1:end-fix(M/2)),'b');%有M/2个数据点延迟
title('滤波信号');xlim([0 0.1])
xlabel('时间/s');

滤波结果

注意：
在设计FIR滤波器中提供了两种滤波方法，即调用filter和conv函数。这两个函数在所设计窗函数阶次比较小的情况下都能够得到精确的效果。但是对于阶次较大的情况（语音信号常态）时，调用filter函数计算可能会出现数据丢失的问题，因为filter是取M+N-1中的前N个数据点，其中包括了M/2个延迟点，因此所得到的结果可能不精准。而对于conv不会，其计算的数据长度为M+N-1，其中正确的输出结果区间为M/2+1~M/2+N，因此在最终的结果输出时调整区间范围即可。可参照代码的最后部分。

总结

1. 在调用相关函数设计滤波器时，一定要注意参数是否归一化；
2. FIR滤波器滤波后会有M/2个数据延迟，需要调整输出区间。