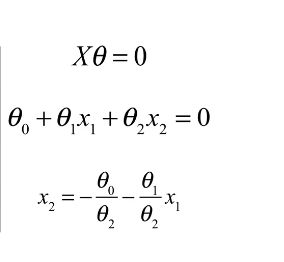吴恩达机器学习ex2

逻辑回归-线性可分

基础知识

线性可分指的是多变量的情况下，可以用直线将两种类别进行划分

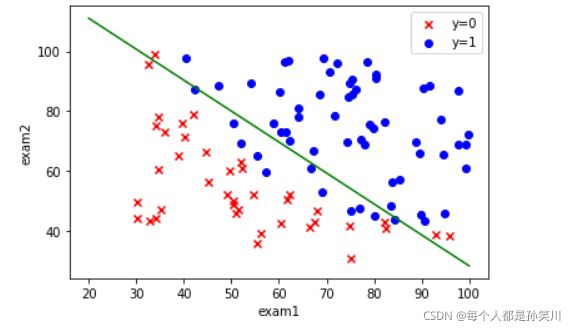
这样我们可以对该模型的函数做出如下假设，由于该分类需要将结果分为0和1，如果还是与上次实验一样使用h=theta@X的话，结果的取值会有不落在0-1之中的。所以添加了一个激活函数sigmoid函数，将theta@X再次做运算，让函数收敛到0和1之间。

关于sigmoid函数

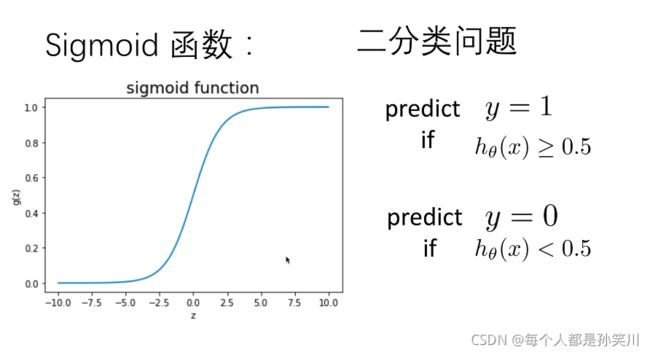
同样的，如果损失函数的计算再使用线性回归中类似的算法的话，可能会出现有多个局部最优解，我们在这里采用的损失函数如下：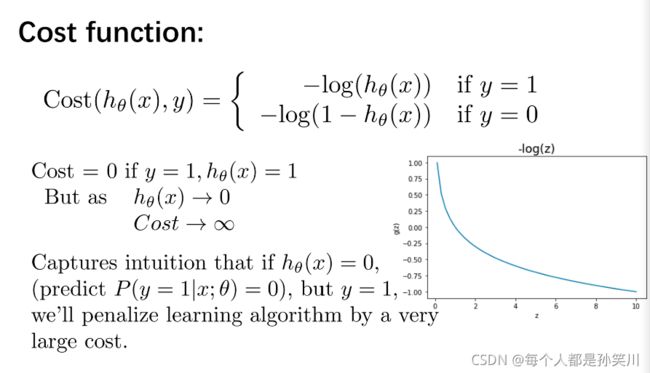
代价函数与批量梯度下降函数如图所示：

实验要求

根据学生的两门成绩，预测该学生是否会被大学录取。 数据集：ex2data1.txt

数据可视化

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
path='./ex2data1.txt'
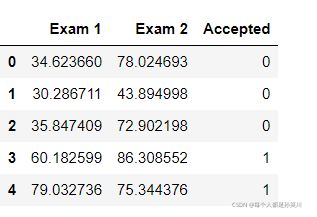
data=pd.read_csv(path,names=['Exam 1','Exam 2','Accepted'])
data.head()

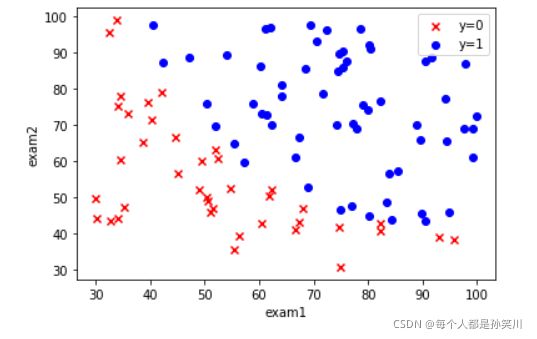
fig,ax=plt.subplots()
ax.scatter(data[data['Accepted']==0]['Exam 1'],data[data['Accepted']==0]['Exam 2'],c='r',marker='x',label='y=0')

ax.scatter(data[data['Accepted']==1]['Exam 1'],data[data['Accepted']==1]['Exam 2'],c='b',marker='o',label='y=1')
ax.legend()
ax.set(xlabel='exam1',
      ylabel='exam2')
plt.show()

构造数据集

def get_Xy(data):
    data.insert(0,'ones',1)
    X_=data.iloc[:,0:-1]
    X=X_.values
    
    y_=data.iloc[:,-1]
    y=y_.values.reshape(len(y_),1)
    
    return X,y
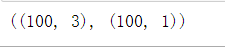
X,y=get_Xy(data)
X.shape,y.shape

构造损失函数

# 定义激活函数
def sigmoid(z):
    return 1/(1+np.exp(-z))

def costFunction(X,y,theta):
    A=sigmoid(X@theta)# 经历激活函数转换之后的结果
    first=y*np.log(A)
    second=(1-y)*np.log(1-A)
    return -np.sum(first+second)/len(X)

theta=np.zeros((3,1))
cost_init=costFunction(X,y,theta)
print(cost_init)

梯度下降函数

def gradientDescent(X,y,theta,iters,alpha):
    m=len(X)
    costs=[]
    
    for i in range(iters):
        A=sigmoid(X@theta)
        theta=theta-(X.T@(A-y))*alpha/m
        cost=costFunction(X,y,theta)
        costs.append(cost)
        if i % 1000==0:
            print(cost)
    return costs,theta

alpha=0.004
iters=200000
costs,theta_final=gradientDescent(X,y,theta,iters,alpha)

theta_final

准确率

def predict(X,theta):
    prob=sigmoid(X@theta)
    return [1 if x>=0.5 else 0 for x in prob]
    
y_=np.array(predict(X,theta_final))
y_pre=y_.reshape(len(y_),1)

acc=np.mean(y_pre==y)
print(acc)

绘制决策边界

coef1=-theta_final[0,0]/theta_final[2,0]
coef2=-theta_final[1,0]/theta_final[2,0]

x=np.linspace(20,100,100)
f=coef1+coef2*x
fig,ax=plt.subplots()
ax.scatter(data[data['Accepted']==0]['Exam 1'],data[data['Accepted']==0]['Exam 2'],c='r',marker='x',label='y=0')

ax.scatter(data[data['Accepted']==1]['Exam 1'],data[data['Accepted']==1]['Exam 2'],c='b',marker='o',label='y=1')
ax.legend()
ax.set(xlabel='exam1',
      ylabel='exam2')

ax.plot(x,f,c='g')
plt.show()

逻辑回归-线性不可分

知识点

线性不可分指的是没有办法用一条直线将类别进行区分

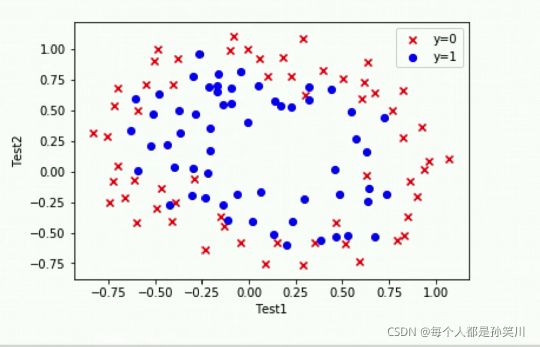
我们无法使用单纯的线性模型来组合特征，我们需要使用复杂的模型来进行组合特征。
我们需要进行特征映射

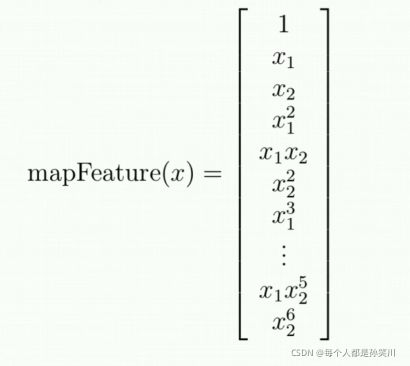
例如：X₁、X₂映射到2阶
1、X₁、X₂、X₁²、X₂²、X₁X₂

正则化线性回归
在损失函数里面添加一个正则项，防止过拟合或者欠拟合

案例介绍

设想你是工厂的生产主管，你要决定是否芯片被接受或者抛弃
数据集：ex2data2.txt,芯片在两次测试中的测试结果

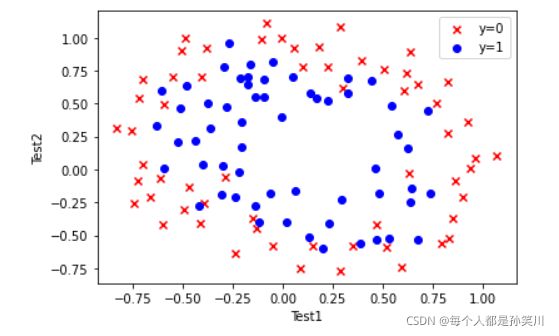
数据可视化

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

path='./ex2data2.txt'
data=pd.read_csv(path,names=['Test1','Test2','Accepted'])
data.head()

fig,ax=plt.subplots()
ax.scatter(data[data['Accepted']==0]['Test1'],data[data['Accepted']==0]['Test2'],c='r',marker='x',label='y=0')

ax.scatter(data[data['Accepted']==1]['Test1'],data[data['Accepted']==1]['Test2'],c='b',marker='o',label='y=1')
ax.legend()
ax.set(xlabel='Test1',
      ylabel='Test2')
plt.show()

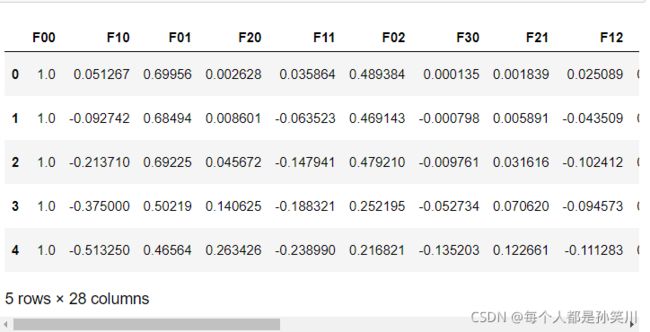
特征映射

def feature_mapping(x1,x2,power):
    data={}
    
    for i in np.arange(power+1):
        for j in np.arange(i+1):
            data['F{}{}'.format(i-j,j)]=np.power(x1,i-j)*np.power(x2,j)
    
    return pd.DataFrame(data)

x1=data['Test1']
x2=data['Test2']
data2=feature_mapping(x1,x2,6)
data2.head()

构造数据集

X=data2.values
y=data.iloc[:,-1].values
y=y.reshape(len(y),1)

正则化损失函数

# 定义激活函数
def sigmoid(z):
    return 1/(1+np.exp(-z))
    
def costFunction(X,y,theta,lamda):
    A=sigmoid(X@theta)# 经历激活函数转换之后的结果
    first=y*np.log(A)
    second=(1-y)*np.log(1-A)
    
    reg=np.sum(np.power(theta[1:],2))*(lamda/(2*len(X)))
    return -np.sum(first+second)/len(X)+reg

theta=np.zeros((28,1))
lamda=1
cost_init=costFunction(X,y,theta,lamda)
print(cost_init)

梯度下降函数

def gradientDescent(X,y,theta,iters,alpha,lamda):
    m=len(X)
    costs=[]
    
    for i in range(iters):
        
        reg=theta[1:]*(lamda*alpha/len(X))
        reg=np.insert(reg,0,values=0,axis=0)
        A=sigmoid(X@theta)
        theta=theta-(X.T@(A-y))*alpha/m-reg
        cost=costFunction(X,y,theta,lamda)
        costs.append(cost)
        if i % 1000==0:
            print(cost)
    return costs,theta

alpha=0.001
iters=200000
lamda=0.1
costs,theta_final=gradientDescent(X,y,theta,iters,alpha,lamda)

准确率

def predict(X,theta):
    prob=sigmoid(X@theta)
    return [1 if x>=0.5 else 0 for x in prob]
    
y_=np.array(predict(X,theta_final))
y_pre=y_.reshape(len(y_),1)

acc=np.mean(y_pre==y)

print(acc)

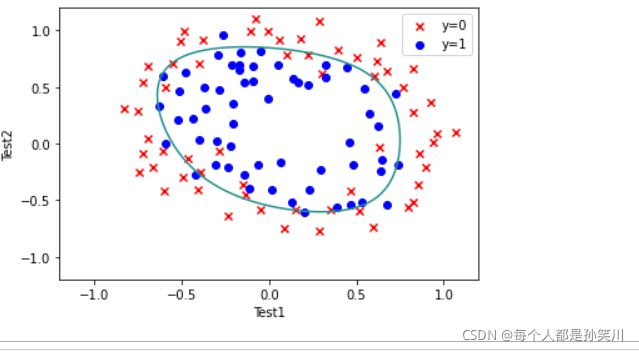
数据可视化

x=np.linspace(-1.2,1.2,200)
xx,yy=np.meshgrid(x,x)

z=feature_mapping(xx.ravel(),yy.ravel(),6).values

zz=z@theta_final

zz=zz.reshape(xx.shape)

fig,ax=plt.subplots()
ax.scatter(data[data['Accepted']==0]['Test1'],data[data['Accepted']==0]['Test2'],c='r',marker='x',label='y=0')

ax.scatter(data[data['Accepted']==1]['Test1'],data[data['Accepted']==1]['Test2'],c='b',marker='o',label='y=1')
ax.legend()
ax.set(xlabel='Test1',
      ylabel='Test2')

plt.contour(xx,yy,zz,0)
plt.show()