图像直方图及其均衡化(matlab自实现)--冈萨雷斯《数字图像处理第三版》
图像直方图及其均衡化(matlab自实现)
-
- 1、显示图像的直方图
- 2、直方图均衡化(matlab自实现)
- 3、直方图Guass(正态)化(matlab自实现)
- 4、以傅里叶变换为例,简单解释两个向量空间和向量基之间的线性变换的概念。
- 5.附代码
- 本文内容原理源自冈萨雷斯《数字图像处理第三版》,代码为自己编写,若有误还请矫正,代码运行效率低,算法拙劣还请见谅。
1、显示图像的直方图
获取一个图像的灰度值直方图,首先需要将 rgb图像转换为灰度图像格式 。遍历灰度图像的每个像素点,统计不同灰度值的个数得到相应的统计数组。采用绘制直方图的方式即可得到该图像的灰度值直方图(如左图所示),与标准的绘制灰度图函数 imhist()所得图像(如右图所示)相比较:
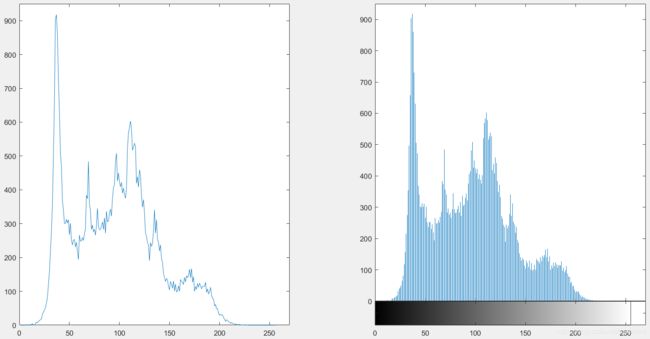
比较两张图 所得的图片可以发现,自制直方图和标准直方图所传达的信息大致无异,都清楚的表现出了该图像的灰度分布直方图。
2、直方图均衡化(matlab自实现)
用r表示待处理图像的灰度, s表示处理之后的图像的灰度。 r的区间为[0 255],r和 s的关系可表示为 s=T(r),T为变换函数,0≤r≤255。假设:
(a)T(r)在区间 0≤r≤255上为单调递增函数
(b)当 0≤r≤255时, 0≤T(r)≤255
接下来就可以做直方图均衡化的工作。懒得打公式

效果如下图所示:

观察直方图均衡化前后两张图像的灰度直方图(如下图)所示:

3、直方图Guass(正态)化(matlab自实现)
自己写的PDF直接截图,公式真的好麻烦。


之前灰暗的地方变得稍微明亮起来,黑白分明更加清晰,说明效果不错。
观察直方图均衡化前后两张图像的灰度直方图 (如下图所示)

直方图的变化并不明显, 推测可能是变换函数处理方面有瑕疵,仍需改进 。
4、以傅里叶变换为例,简单解释两个向量空间和向量基之间的线性变换的概念。
在向量空间中,任意一个元素都可以唯一的表示成基向量的线性组合,基向量就是向量基底的一个特殊的子集。使用基底可以便利地描述向量空间。比如说,考察从一个向量空间 V射出的线性变换 f,可以查看这个变换作用在向量空间的一组基 α 上的效果。 掌握了 f(α),就等于掌握了 f对 V中任意元素的效果。
著名的傅里叶变换就是在向量空间的线性变换。 已知傅里叶变换表达式为:


记得点赞
5.附代码
clear all;
close all;
clc;
a=imread('visual.jpg');
a = rgb2gray(a);
b = hist(a);
figure(1);
subplot(1,2,1);
plot(b);
axis([0 270 0 950]);
subplot(1,2,2);
imhist(a);
c=histequ(a);;
figure(2);
subplot(1,2,1);
imshow(a);
title("原图");
subplot(1,2,2);
imshow(c);
title("直方图均衡化后的图");
figure(3);
subplot(1,2,1);
imhist(a);
title("原图灰度直方图");
subplot(1,2,2);
d=histeq(a);
imhist(d);
title("直方图均衡化后的灰度直方图");
figure(4)
ee=histgauss(a);
subplot(1,2,1);
imshow(a)
title("原图");
subplot(1,2,2);
imshow(ee);
title("直方图正态分布化后的图");
figure(5)
subplot(1,2,1)
imhist(a)
title("原图灰度直方图");
subplot(1,2,2)
imhist(ee)
title("直方图正态分布化后的灰度直方图");
function histogram = hist(a)
[h ,w]=size(a);
histogram = zeros(1,256);
for i=1:h
for j = 1:w
k = round(a(i,j));
histogram(1,k)=histogram(1,k)+1;
end
end
end
function histogram = histequ (a)
[h ,w]=size(a);
capacity = h*w;
r_pdf = hist(a)/capacity;
s_output = size(a);
for i=1:h
for j = 1:w
prw = 0;
for r=1:a(i,j)
prw=r_pdf(r)+prw;
end
s_output(i,j)=ceil(255*prw);
end
end
histogram=uint8(s_output);
end
function histogram = histgauss(a)
a=histeq(a);
[h ,w]=size(a);
a_pdf = zeros(1,256);
for i=1:h
for j = 1:w
k = round(a(i,j))+1;
a_pdf(1,k)=a_pdf(1,k)+1;
end
end
a_pdf=a_pdf/(h*w);
Gz=zeros(h,w);
for i=1:h
for j = 1:w
prw = 0;
for r=1:a(i,j)
temp = exp(double(-a_pdf(r)*a_pdf(r)/2));
prw=prw+temp;
end
Gz(i,j)=round(255*prw/(sqrt(2*pi)*100));
end
end
histogram =uint8(Gz);
end