基于混沌算法的图像加密技术（一）

1.什么是混沌？

混沌（chaos）是一个动力学的概念，指确定性动力学系统因对初值敏感而表现出来的不可预测以及类随机的规则。1963年美国气象学家洛伦兹深入研究大气运动规律，结合数学分析，并且给出了一个对应的数学方程这组方程我们将在后面给出。
初值敏感性是混沌系统最重要的特征之一，所以理解他对我们理解混沌系统至关重要。初值敏感性指的是初始条件下微小的变化能带动整个系统长期的巨大连锁反应，最好的例子就是蝴蝶效应。一只南美洲亚马逊河流域热带雨林中的蝴蝶，偶尔扇动几下翅膀，可以在两周以后引起美国得克萨斯州的一场龙卷风。无独有偶洛伦兹系统的吸引子图恰好像一个蝴蝶。下面我们给出了洛伦兹方程以及其吸引子图。

当p=10、r=28、b=8/3。该系统进入混沌状态。

使用到的matlab代码如下：

function dydt = lorenz_diff(t,y)
%lorenz_diff方程代码
dydt = [ -10*(y(1)-y(2));
          30*y(1)-y(1)*y(3)-y(2);
          -8/3*y(3)+y(1)*y(2)];  

y0 = [0,2,9];          
[t,y] = ode45('lorenz_diff',[0,200],y0); 
plot(y(:,1),y(:,3));
grid on;

2.分岔图

对于一般的数学公式，一般可以通过拟合的方法得到该模型的运动轨迹，换句话说给你1000个值我极有可能通过拟合再画线的方法或者通过人工智能训练的方法“猜”到第1001个值。
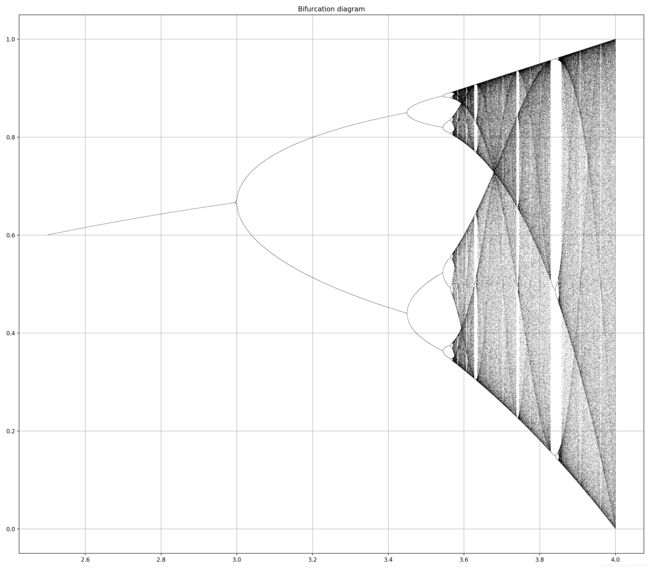
但是对于一个混沌系统而言，当系统进入混沌态后；成功对值进行预测的可能性非常低甚至不可能。（其实对密码学而言，如果在一定时间内不能有效破译密码也是没有意义的）让我们举一个简单的例子下图是一个Logistic模型的分岔图，在看分岔图前我们先解释一下分岔。

根据动力学的理论，分岔的概念可以理解成这样一种现象，即动力学系统的一个参数的连续变化引起了系统行为突然的急剧反应，从而导致运动性质改变。将一种运动模式变成了另一种运动模式。

Logistic分岔图的python代码

# 代码参考：https://ipython-books.github.io/121-plotting-the-bifurcation-diagram-of-a-chaotic-dynamical-system/
import matplotlib.pyplot as plt
import numpy as np

# 迭代次数
iterations = 1000
# 取多少个点
last = 100
# 取n个点
n = 20000
r = np.linspace(2.5, 4.0, n)
# x初值
x = 0.2 * np.ones(n)
fig, ax1 = plt.subplots(figsize=(16, 14), dpi=200)
for i in range(iterations):
    x = r * x * (1 - x)
    # 输出周期点
    if i >= (iterations - last):
        ax1.plot(r, x, ',k')

ax1.set_title("Bifurcation diagram")
plt.grid(True)
plt.savefig('Bifurcation_diagram.png')
plt.show()

2.初值敏感性

当对Logistic的r=4(系统参数)、初值为0.6，初始值偏差为0.001时，两个值所表现出来的初值敏感性

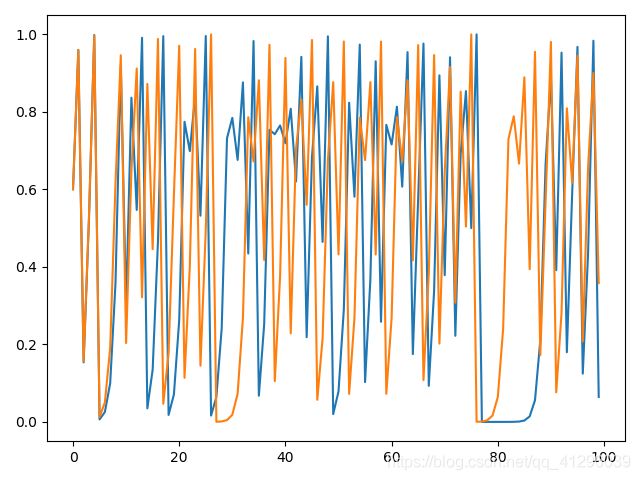
实验代码如下：

import matplotlib.pyplot as plt
import numpy as np

# 初始值 (0-1)
x0 = 0.6
# 初始值偏差
b = 0.001
# x_t+1 = R*x_t*(1-x_t)
R = 4
# 数组长度
size = 100
t = np.arange(size)
# x1
x1 = np.zeros(size)
x1[0] = x0
# x2
x2 = np.zeros(size)
x2[0] = x0 + b  # 加上初始值偏差
for i in range(1, size):
    x1[i] = R * x1[i - 1] * (1 - x1[i - 1])
    x2[i] = R * x2[i - 1] * (1 - x2[i - 1])

plt.plot(t, x1)
plt.plot(t, x2)
# 要放在plt.show()前，不然保存的就是空白图片
plt.show()

3.遍历性

我们通过Logistic连续迭代了2000次，分析了这些值的分布情况并绘制了直方图。

分布	0.0-0.1	0.1-0.2	0.2-0.3	0.3-0.4	0.4-0.5	0.5-0.6	0.6-0.7	0.7-0.8	0.8-0.9	0.9-1.0
个数	426	187	148	119	143	126	122	141	179	408
比例	21.3%	9.35%	7.4%	5.95%	7.15%	6.3%	6.1%	7.05%	8.95%	20.4%

分布直方图

观察上图的分布情况，其实Logistic映射的随机分布情况并不是十分好，对于其他的初值Logistic映射也有类似的情况。几乎都是呈现出一种中间小两头大的情况。其实不仅仅是Logistic映射，像这样分布不随机的情况在低维混沌系统也是经常出现。即便如此，Logistic作为比较简单的混沌映射依然可以完成很多简单的加密技术。

4.如何利用到图片加密上？

简单来说，像这样的lena图而言，其可以转换成一个值为[0，255]，256×256大小的矩阵。

对于我们而言，组成这个图最基本的要素是像素值的大小和像素值的位置。图片中的像素值或者位置的改变都可能引发我们对图片的理解出现偏差。
如果有这么一个”图片破坏者“，其工作就可以是改变图像像素的位置或者改变图片像素值。他通过成程序随机数利用随机数改变像素值或者像素位置那么轻而易举就可以使得这个图片面目全非。但是这个”图片破化者“只能破坏图片却不能还原图片。因为任何程序都没有机会再次生成同样的随机数。
但是对于混沌系统而言，混沌系统也具有十分优越的伪随机性，这样的随机性能够有效的对这张图片进行破坏，使得通过非法手段获取图片的无法理解这张图。而这样的”随机性“对于图片的加密者是完全可再恢复的。同时出色的初值敏感性能防止绝大数的暴力破解，遍历性和随机性能有效的预防差分攻击和统计学攻击。