基于householder变换的QR分解

QR分解的定义

m和n为任意正整数，给出$A\in C^{m\times n}$,任意矩阵都可以不需要满秩等条件，则$A$可分解为$A=QR$,其中$Q\in C^{m\times m}$为一正交阵，$R\in C^{m\times n}$为一上三角阵。
存在性：
唯一性：

householder变换

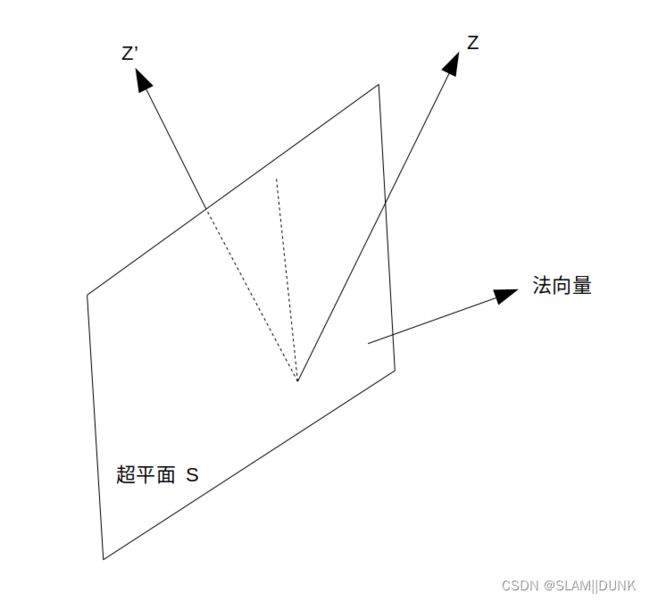
考虑一个位于$R^n$空间的超平面，以向量$\omega$为法向量，该超平面可表示为：
$$S=[x|{\omega }^{T}x=0,\forall x\in R^n]$$
该超平面是由无数垂直与$\omega$的向量组成的，并且是$R^n$的子空间，其维度/秩为n-1,因为，对于${\omega }^{T}x=0$,有下列齐次线性方程组成立：
$$\left[\begin{array}{c}{x}_1\\ x_2\\ .\\ .\\ x_n\end{array}\right]\omega =0$$
对于该$AX=0$,有唯一解，因此$rank(A)=n-1$。

对于任意模长为1的法向量$\omega \in R^n$,有反射矩阵 $H=I-2\omega {\omega }^T$，显然，该反射矩阵为一对称正交阵，即满足：$H=H^T$, $HH=I$

将该反射矩阵$H$作用与任意一个向量$Z\in R^n$,即$HZ$,将得到一个与$Z$关于$H$超平面S对称的向量$Z^{\prime }$，如上图所示，这种反射变换即householder变换。

基于householder变换的QR分解

核心推论：
任意两个范数相同的向量$z_1,z_2$，$\Vert z_1{\Vert }_2=\Vert z_2{\Vert }_2,$存在一个超平面$S$,使得$z_1$和$z_2$关于超平面$S$对称，因此，有householder变换矩阵$H$,使得 $z_1=H{z}_2$.

基于此推论，我们可以找到一个householder变换矩阵，使得矩阵A的最左边的向量$v$变为仅第一行元素非0而其他元素为0的向量$\left[\begin{array}{c}x\\ 0\\ .\\ .\\ 0\end{array}\right]$,$x=\Vert v{\Vert }_2,$于是迭代此操作将矩阵A变换为一个上三角矩阵。算法思路简单，下面给出C++实现：

/**
 * @brief: QR分解
 * @details 将任意m.n维矩阵 A 分解为 Q(m.m) x R(m.n) 
 * @param {MatrixXd const&} m_in 输入矩阵
 * @param {MatrixXd&} Q Q正交矩阵
 * @param {MatrixXd&} R 上三角矩阵
 * @return {*}
 */
void HouseholderQR(Eigen::MatrixXd const& m_in, Eigen::MatrixXd& Q, Eigen::MatrixXd& R) {
    int row = m_in.rows();
    int col = m_in.cols();
    R = m_in;  
    Eigen::MatrixXd P = Eigen::MatrixXd::Identity(row, row);

    for (int i = 0; i < col; i++) {
        if (i == row) break;  
        Eigen::VectorXd v = R.block(i, i, row - i, 1);
        double roi = v.norm();
        Eigen::VectorXd base = Eigen::MatrixXd::Zero(row - i, 1);
        base(0) = 1;   
        Eigen::VectorXd omega_v = v - roi * base;  
        omega_v.normalize();  
        R.block(i, i, row - i, col - i) = R.block(i, i, row - i, col - i) - 
            2 * omega_v * (omega_v.transpose() * R.block(i, i, row - i, col - i));
        P.block(i, 0, row - i, row) =  P.block(i, 0, row - i, row) - 
        2 * omega_v * (omega_v.transpose() * P.block(i, 0, row - i, row));
    }
    Q = P.transpose();
}

总的时间复杂度 $O(n^3)$。
注意，代码中

2 * omega_v * (omega_v.transpose() * R.block(i, i, row - i, col - i))

不要写成

2 * omega_v * omega_v.transpose() * R.block(i, i, row - i, col - i)

因为，前一种写法先执行(omega_v.transpose() * R.block(i, i, row - i, col - i))，为向量和矩阵相乘，时间复杂度$O(N^2)$,然后再将omega_v和括号里运算的结果进行相乘，为列向量乘行向量，时间复杂度为$O(N^2)$,因此叠加后总的时间复杂度依然为$O(N^2)$。
而第二种写法先执行omega_v * omega_v.transpose() 变成了一个矩阵，接下来就是矩阵与矩阵相乘，时间复杂度为$O(N^3)$,因此我们将运算拆分成矩阵与向量的乘法，而不是矩阵与矩阵的乘法。

实验：

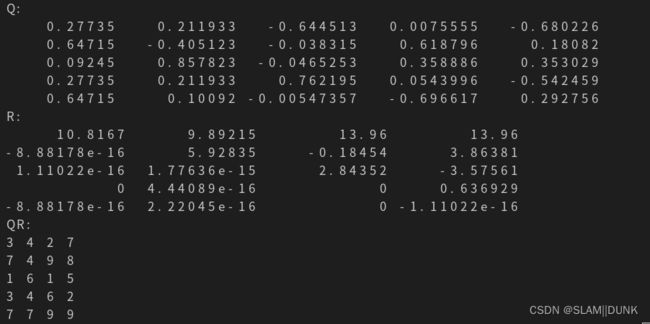
1、超定 m > n

Eigen::Matrix<double, 5, 4> m_in;
 m_in <<   3, 4, 2, 7,
                     7,4,9,8,
                     1,6,1,5,
                     3,4,6,2,
                     7,7,9,9;

结果：
2、方阵 m = n

    Eigen::Matrix<double, 4, 4> m_in;
    m_in <<   3, 4, 2, 7,
                        7,4,9,8,
                        1,6,1,5,
                        3,4,6,2;

结果：

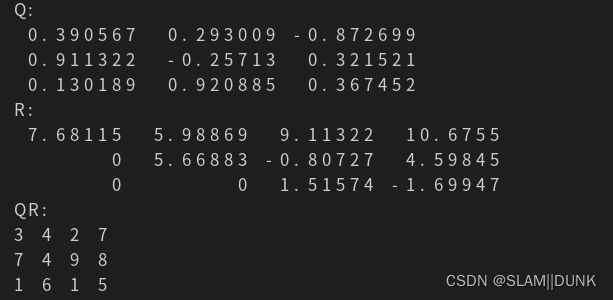
3、欠定 m < n

    Eigen::Matrix<double, 3, 4> m_in;
    m_in <<   3, 4, 2, 7,
                        7,4,9,8,
                        1,6,1,5;

总结：

基于householder变换的QR分解对于任意维度的矩阵都适用，对于任意m行n列的矩阵，QR分解将其分解为
m行m列的正交矩阵Q以及m行n列的上三角矩阵R。