双目视觉之对极几何

对极几何(Epipolar Geometry)

                                                本文为我翻译了一篇国外的ppt，并在此基础上进行了修改并写了自己的见解。

先思考一个问题：用两个相机在不同的位置拍摄同一物体，如果两张照片中的景物有重叠的部分，我们有理由相信，这两张照片之间存在一定的对应关系（模拟人眼）。本节的任务就是如何描述它们之间的对应关系，描述工具是对极几何 ，它是研究立体视觉的重要数学方法。要寻找两幅图像之间的对应关系，最直接的方法就是逐点匹配，如果加以一定的约束条件对极约束(epipolar constraint)，搜索的范围可以大大减小。从2D平面搜索转为1D直线搜索，搜索速度也会提高

先回顾简单的立体成像系统。这是一种特殊情况，两相机成像平面并排，左右相机公式即为图像物理坐标系和相机坐标系的转换关系，视差 d = xl - xr（xl和xr是在图像物理坐标系上，原点在Z轴）

根据三角形相似原理，能够得到   （xr是负数，所以是减号） 

实际上，跟一般的情况，两个相机肯定不可能完全对准，它们坐标无任何约束关系，相机的内部参数可能不同，甚至是未知的。要刻画这种情况下的两幅图像之间的对应关系，需要引入两个重要的概念——对极矩阵(Epipolar Matrix)和基本矩阵(Fundamental Matrix)

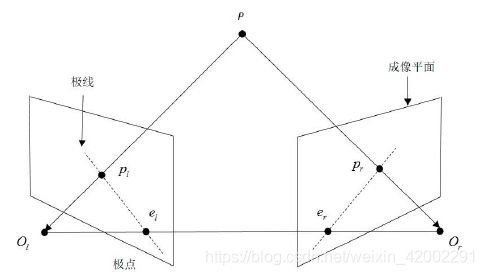
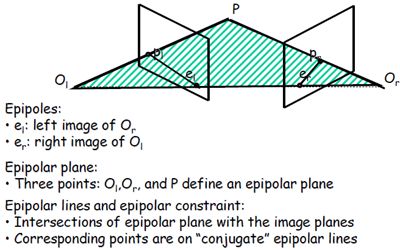
一些概念：P是空间点，pl和pr是成像点，el和er是极点（也就是光心Ol和Or连线和成像面的交点），点P，Ol和Or组成的平面叫极平面，pl和el的连线以及pr和er的连线叫极线（也就是极平面和成像面的交线），级线约束就是两极线上点的对应关系。（左相机上一点，在右相机上的对应点肯定在其极线上）

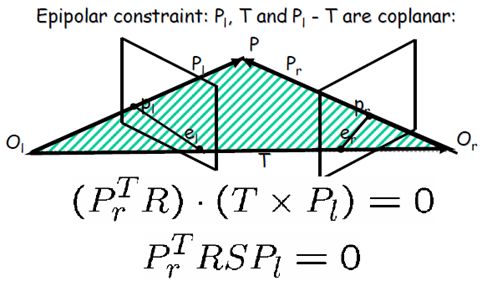
两相机坐标系间的转换关系 (R是左相机相对右相机的转换矩阵，向量Pl-T算出Pr是在左相机坐标系的，乘R后的Pr是在右相机坐标系的)，这里的R是正交矩阵（矩阵的逆等于其转置）。

三个向量共线，混合积为0（或者理解成T叉乘Pl为极平面的法向量n，n和Pl垂直，点积为0） 

 将叉积写成矩阵的形式，这是个3x1的矩阵，再分离出S（用到了计算叉积的公式）

令E=RS，E就是定义的本质矩阵(Essential Matrix)，右下角的方程即左像点和右像点的约束关系。

本质矩阵E的性质：has rank 2（秩为2），and depends only on the EXTRINSIC Parameters (R & T)(仅依赖于外部参数R和T，R是左相机相对右相机的转换矩阵Rotation，T是点Ol在Or中的坐标，也就是平移向量Translation，不要看向量方向，这是根据他公式来的，这里左相机相当于动系，如果右相机是动系的话，我也推了下，结果是一样的，而且还少了正交矩阵的逆是转置那一步）

结合成像的关系（图像物理坐标系和相机坐标系间）小写pr和pl是在图像物理坐标上，大写的是在相机坐标系上。

方框中的方程被称为：Longuet-Higgins equation

设l为像平面上一条直线，则有直线方程 au+bv+c=0 ，由点线结合关系有

因此能推出下式。（注意：我认为下面这个直线lr是在图像物理坐标系下的）

这样就可以用几何的观点来解释上述方程：左像平面上的一点pl乘本质矩阵E，结果为一条直线，该直线是右像平面上pl对应点的极线，即pr就在此极线上。同理有

Remember: epipoles belong to the epipolar lines  注意到极点也在极线上

 And they belong to all the epipolar lines  极点在所有的极线上，也就是无论pl和pr怎么变，上面两式都得0，则有

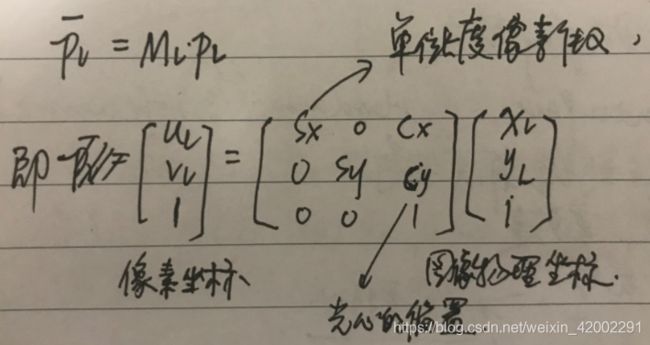
本质矩阵E采用的是相机的外部参数，也就是说采用相机坐标(The essential matrix uses CAMERA coordinates)，如果要分析数字图像，则要考虑像素坐标(u,v)，此时需要用到内部参数(To use image coordinates we must consider the INTRINSIC camera parameters)

short version: The same equation works in pixel coordinates too!  转到图像像素坐标系上考虑有 （杠表示在图像像素坐标系下）

F的一些性质如下：has rank 2   秩为2，depends on the INTRINSIC and EXTRINSIC Parameters (f, etc ; R & T)   取决于内参和外参

Analogous to essential matrix. The fundamental matrix also tells how pixels (points) in each image are related to epipolar lines in the other image.  和本质矩阵E类似，基本矩阵F还说明了每个图像中的像素（点）如何与另一个图像中的极线相关。

再用到前面提到的点线关系，右像平面像点在右极线上，则有以下关系 （lr杠是在图像像素坐标系下）

由此可知，通过在左像平面获得像素点坐标，乘上基本矩阵F，可右平面极线的方程（a，b，c）