Cholesky分解—概率密度分布及累计概率分布（完整代码分享）

Cholesky分解是一种分解矩阵的方法, 在线性代数中有重要的应用。Cholesky分解把矩阵分解为一个下三角矩阵以及它的共轭转置矩阵的乘积（那实数界来类比的话，此分解就好像求平方根）。与一般的矩阵分解求解方程的方法比较，Cholesky分解效率很高。

分解条件：

1、矩阵中的元素共轭对称（复数域的定义，类比于实数对称矩阵）。

2、正定（矩阵域，类比于正实数的一种定义）。

代码：

clc;
clear all;

Cx3=[1.0 0.5;
     0.5 1.0];
Cx1=[1.0 0.5 0.8 0.7 0.6;
     0.5 1.0 0.7 0.6 0.8;
     0.8 0.7 1.0 0.5 0.6;
     0.7 0.6 0.5 1.0 0.9;
     0.6 0.8 0.6 0.9 1.0];
Cx2=[1.0 0.5 0.8 0.7 0.6 0.4;
     0.5 1.0 0.7 0.6 0.8 0.5;
     0.8 0.7 1.0 0.5 0.6 0.5;
     0.7 0.6 0.5 1.0 0.9 0.6;
     0.6 0.8 0.6 0.9 1.0 0.6;
     0.4 0.5 0.5 0.6 0.6 1.0]; 
 %正定矩阵的Cholesky分解 
[m,n]=size(Cx1); 
if m~=n  %判断输入的矩阵是不是方阵 
    disp('输入的矩阵不是方阵，请重新输入'); 
    return; 
end 
for i=1:n  %判断输入的矩阵是不是对称矩阵 
    for j=1:n 
        if Cx1(i,j)~=Cx1(j,i) 
            disp('输入的方阵不是对称矩阵，请重新输入'); 
            return; 
        end 
    end 
end 
d=eig(Cx1); %根据方阵的特征值判定是不是正定矩阵 
for i=1:n 
    if d(i)==0 
        disp('输入的矩阵不是正定矩阵，请重新输入'); 
        return; 
    else 
        break; 
    end 
end 
disp('输入的矩阵可以进行Cholesky分解'); %如果是正定矩阵，可以进行下面的分解操作 
R1=chol(Cx1,'lower');

randn('state', sum(100*clock)); 
%利用时钟设置随机种子，这样每次产生的随机数就不同了 
N=1000; 
% 设置样本个数 
W1=zeros(5,N);
WW1=zeros(5,N);
for i=1:N
    W1(:,i)=randn(5,1); 
end
WW1(1,:)=W1(1,:).*0.45+4.5;
WW1(2,:)=W1(2,:).*0.63+3.7;
WW1(3,:)=W1(3,:).*0.58+5.3;
WW1(4,:)=W1(4,:).*0.51+4.9;    
WW1(5,:)=W1(5,:).*0.56+4.2;  
Z1=R1*W1;
rouMW1=corrcoef(W1');
rouMZ1=corrcoef(Z1');

Ls1=zeros(5,N);
for p=1:5
    maxZ1=max(Z1(p,:));
    k=1;
    for q=1:N
        [minZ locZ]=min(Z1(p,:));
        Ls1(p,locZ)=k;
        k=k+1;
        Z1(p,locZ)=maxZ1+1;
    end
end
LLs1=Ls1;

x1=zeros(5,N);
for i=1:N
    sx1=(i-0.5)/N;
    x1(1,i)=norminv(sx1,4.5,0.45);
    x1(2,i)=norminv(sx1,3.7,0.63);
    x1(3,i)=norminv(sx1,5.3,0.58);
    x1(4,i)=norminv(sx1,4.9,0.51);
    x1(5,i)=norminv(sx1,4.2,0.56);    
end

S1=zeros(5,N);
for i=1:5
    tx1=x1(i,:);
    tLs1=LLs1(i,:);
    maxy1=max(tx1);
    maxtLs1=max(tLs1);
    for p=1:N
        [C1 D1]=min(tx1);
        [C2 D2]=min(LLs1(i,:));
        tLs1(1,D2)=C1;
        tx1(1,D1)=maxy1+1;
        LLs1(i,D2)=maxtLs1+1;
    end
    S1(i,:)=tLs1;
end
rouMS1=corrcoef(S1');


 %正定矩阵的Cholesky分解 
[m,n]=size(Cx2); 
if m~=n  %判断输入的矩阵是不是方阵 
    disp('输入的矩阵不是方阵，请重新输入'); 
    return; 
end 
for i=1:n  %判断输入的矩阵是不是对称矩阵 
    for j=1:n 
        if Cx2(i,j)~=Cx2(j,i) 
            disp('输入的方阵不是对称矩阵，请重新输入'); 
            return; 
        end 
    end 
end 
d2=eig(Cx2); %根据方阵的特征值判定是不是正定矩阵 
for i=1:n 
    if d2(i)==0 
        disp('输入的矩阵不是正定矩阵，请重新输入'); 
        return; 
    else 
        break; 
    end 
end 
disp('输入的矩阵可以进行Cholesky分解'); %如果是正定矩阵，可以进行下面的分解操作 
R2=chol(Cx2,'lower');

randn('state', sum(100*clock)); 
%利用时钟设置随机种子，这样每次产生的随机数就不同了 
% 设置样本个数 
W2=zeros(6,N);
WW2=zeros(6,N);
for i=1:N
    W2(:,i)=randn(6,1); 
end
    WW2(1,:)=W2(1,:).*0.45+4.5;
    WW2(2,:)=W2(2,:).*0.63+3.7;
    WW2(3,:)=W2(3,:).*0.58+5.3;
    WW2(4,:)=W2(4,:).*0.51+4.9;    
    WW2(5,:)=W2(5,:).*0.56+4.2;
    WW2(6,:)=W2(6,:).*0.47+4.7;
Z2=R2*W2;
rouMW2=corrcoef(W2');
rouMZ2=corrcoef(Z2');

Ls2=zeros(6,N);
for p=1:6
    hig=max(Z2(p,:));
    k=1;
    for i=1:N
        [b c]=min(Z2(p,:));
         Ls2(p,c)=k;
        k=k+1;
        Z2(p,c)=hig+1;
    end
end
LLs2=Ls2;

x2=zeros(6,N);
for i=1:N
    tt=(i-0.5)/N;
    x2(1,i)=norminv(tt,4.5,0.45);
    x2(2,i)=norminv(tt,3.7,0.63);
    x2(3,i)=norminv(tt,5.3,0.58);
    x2(4,i)=norminv(tt,4.9,0.51);
    x2(5,i)=norminv(tt,4.2,0.56);  
    x2(6,i)=norminv(tt,4.7,0.47);
end


for i=1:6
    y2=x2(i,:);
    bb2=LLs2(i,:);
    hig1=max(y2);
    hig2=max(bb2);
    for p=1:N
        [C1 D1]=min(y2);
        [C2 D2]=min(LLs2(i,:));
       bb2(1,D2)=C1;
    y2(1,D1)=hig1+1;
       LLs2(i,D2)=hig2+1;
end
yy2(i,:)=bb2;
end

ccc22=corrcoef(yy2');

%for i=1:6
%[f,xi]=ksdensity(yy2(i,:));
%绘制图形
%figure(i);
%subplot(2,1,1);
%plot(yy(i,:));
%title('样本数据(Sample Data)')
%subplot(2,1,2);
%plot(xi,f);
%title('概率密度分布(PDF)')
%end


 %正定矩阵的Cholesky分解 
[m,n]=size(Cx3); 
if m~=n  %判断输入的矩阵是不是方阵 
    disp('输入的矩阵不是方阵，请重新输入'); 
    return; 
end 
for i=1:n  %判断输入的矩阵是不是对称矩阵 
    for j=1:n 
        if Cx3(i,j)~=Cx3(j,i) 
            disp('输入的方阵不是对称矩阵，请重新输入'); 
            return; 
        end 
    end 
end 
d3=eig(Cx3); %根据方阵的特征值判定是不是正定矩阵 
for i=1:n 
    if d(i)==0 
        disp('输入的矩阵不是正定矩阵，请重新输入'); 
        return; 
    else 
        break; 
    end 
end 
disp('输入的矩阵可以进行Cholesky分解'); %如果是正定矩阵，可以进行下面的分解操作 
R3=chol(Cx3,'lower');

randn('state', sum(100*clock)); 
%利用时钟设置随机种子，这样每次产生的随机数就不同了 
% 设置样本个数 
W3=zeros(2,N);
WW3=zeros(2,N);
for i=1:N
    W3(:,i)=randn(2,1); 
end
for i=1:N
    WW3(:,i)=wblrnd(9.0,2.15,2,1); 
end


Z3=R3*W3;
ccc03=corrcoef(W3');
ccc03
ccc13=corrcoef(Z3');
ccc13

aa3=zeros(2,N);
Ls3=zeros(2,N);
for p=1:2
hig=max(Z3(p,:));
k=1;
for i=1:N
[b c]=min(Z3(p,:));
Ls3(p,c)=k;
k=k+1;
Z3(p,c)=hig+1;
end
end
LLs3=Ls3;

x=zeros(2,N);
for i=1:N
    tt=(i-0.5)/N;
    x3(1,i)=wblinv(tt,9.0,2.15);
    x3(2,i)=wblinv(tt,9.0,2.15);   
end


for i=1:2
y3=x3(i,:);
bb3=LLs3(i,:);
hig1=max(y3);
hig2=max(bb3);

for p=1:N
[C1 D1]=min(y3);
[C2 D2]=min(LLs3(i,:));
bb3(1,D2)=C1;
y3(1,D1)=hig1+1;
LLs3(i,D2)=hig2+1;
end
yy3(i,:)=bb3;
end

ccc23=corrcoef(yy3');
ccc23

YY=[S1;yy2;yy3];
YY
ccc3=corrcoef(YY');
ccc3
for i=1:N
F(1,i)=(S1(1,i)+S1(2,i)+S1(3,i)+S1(4,i)+S1(5,i))+(yy2(1,i)+yy2(2,i)+yy2(3,i)+yy2(4,i)+yy2(5,i)+yy2(6,i))+(yy3(1,i)+yy3(2,i));
FF(1,i)=(WW1(1,i)+WW1(2,i)+WW1(3,i)+WW1(4,i)+WW1(5,i))+(WW2(1,i)+WW2(2,i)+WW2(3,i)+WW2(4,i)+WW2(5,i)+WW2(6,i))+(WW3(1,i)+WW3(2,i));
end
minF=min(F);
maxF=max(F);
del=(maxF-minF)/5;
pp=linspace(minF-del,maxF+del,100) ;
[f1,xi1]=ksdensity(F,pp,'function','pdf');
[f2,xi2]=ksdensity(FF,pp,'function','pdf');
figure(1);
plot(xi1,f1,'r');
hold on
plot(xi2,f2,'b');
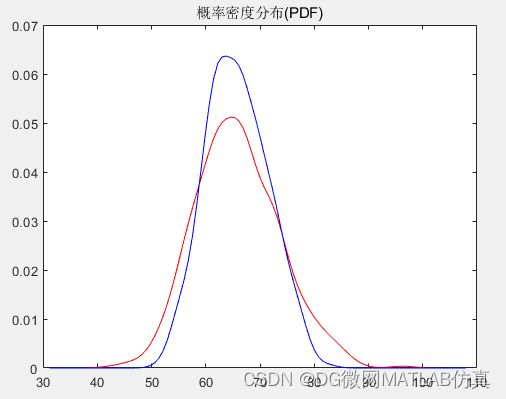
title('概率密度分布(PDF)')


pp=linspace(minF-del,maxF+del,100) ;
[f11,xi11]=ksdensity(F,pp,'function','cdf');
[f22,xi22]=ksdensity(FF,pp,'function','cdf');
figure(2);
plot(xi11,f11,'r');
hold on
plot(xi22,f22,'b');
title('累积概率分布')

结果：