零基础学习Transformer:AttentionLayer and Self-AttentionLayer
Transformer Model
- Transformer是一个Seq2Seq模型,有一个encoder和一个decoder
- Transformer不是RNN,没有循环的结构,只有attention和全连接层(dense layers)
- 实验效果好,优于RNNs
Attention for RNN
Attention for Seq2Seq Model,where are an encoder and a decoder.

输入m个向量,encoder将输入信息压缩到m个状态向量 h 1 , . . . , h m h_1,...,h_m h1,...,hm中,最后一个状态信息 h m h_m hm是对所有输入信息的一个概括。decoder是一个文本生成器,生成m个状态 s 1 , . . . , s j − 1 s_1,...,s_{j-1} s1,...,sj−1,第 s j s_j sj是第m+1个状态。
计算:将 S j S_j Sj与所有encoder中的m个状态信息 h 1 , . . . , h m h_1,...,h_m h1,...,hm做对比,用align函数计算相关性, α i j = align ( h i , s j ) \alpha_{i j}=\operatorname{align}\left(\mathbf{h}_{i}, \mathbf{s}_{j}\right) αij=align(hi,sj),将计算结果 α i j \alpha_{i j} αij作为权重。
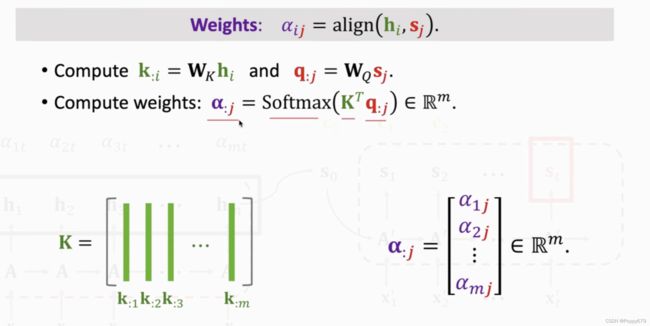
α : j \alpha_{: j} α:j中的元素全都介于0和1之间,并且相加和为1.以上能得到m个权重。
对 s j s_j sj和 h i h_i hi做线性变换,query的作用是匹配key值,key的作用是被query匹配。通过 q : j q_{: j} q:j与 K T K^T KT中每个元素的匹配,得到的 α : j \alpha_{: j} α:j越大,则匹配程度越高。

其中, W q , W K , W V W_q, W_K,W_V Wq,WK,WV是该层的参数,需要系统学习获得。
计算流程:
- 将decoder中的状态向量 s j s_j sj映射到query向量
- 将encoder中 h 1 , . . . , h m h_1,...,h_m h1,...,hm向量映射到m个key向量
- 用矩阵 K K K与 q q q计算出m维的权重向量 α : j \alpha_{: j} α:j,向量 α : j \alpha_{: j} α:j中元素分别是 α 1 j , α 2 j , . . . , α m j \alpha_{1 j},\alpha_{2 j},...,\alpha_{m j} α1j,α2j,...,αmj,每一个元素都对应一个 h h h。
- 计算value向量 v : i v_{: i} v:i,encoder的第i个状态向量 h i h_i hi与参数矩阵 W v W_v Wv,对m个状态向量都做这样的变化,得到m个value值 v 1 , v 2 , . . . , v m v_1,v_2,...,v_m v1,v2,...,vm。每一个value向量都对应一个 h h h
- m个 α \alpha α做权重,对m个value向量做加权平均,并将结果作为新的context向量 c j c_j cj。计算公式: c j = α 1 j v : 1 + ⋯ + α m j v : m \mathrm{c}_{j}=\alpha_{1 j} \mathbf{v}_{: 1}+\cdots+\alpha_{m j} \mathbf{v}_{: m} cj=α1jv:1+⋯+αmjv:m
Attention without RNN
剥离RNN就可以得到attention层和self-attention层。
首先考虑基于Seq2Seq的模型,这样的模型有一个编码器和一个解码器。举个例子:想要把英语翻译成德语。那么英语单词就是encoder的输入序列 x 1 , x 2 , . . . , x m x_1,x_2,...,x_m x1,x2,...,xm,decoder依次生成德语单词作为下一轮decoder的输入序列 x 1 ′ , x 2 ′ , . . . , x t ′ x'_1,x'_2,...,x'_t x1′,x2′,...,xt′,接下来新生成的德语单词会成为第t+1个输入。

如果不用RNN,只考虑attention。首先利用encoder的输入 x 1 , x 2 , . . . , x m x_1,x_2,...,x_m x1,x2,...,xm来计算key和value向量,于是 x 1 x_1 x1就被映射成了 k : 1 k_{:1} k:1和 v : 1 v_{: 1} v:1…由此得到m个k和m个v向量。
接着将decoder的输入向量 x 1 ′ , x 2 ′ , . . . , x t ′ x'_1,x'_2,...,x'_t x1′,x2′,...,xt′做线性变换,将其映射道query向量 q : j q_{: j} q:j

接着计算权重。将 q : 1 q_{: 1} q:1与m个k向量做对比(比较相关性),计算出权重 α \alpha α,公式: α : 1 = Softmax ( K T q : 1 ) ∈ R m \alpha_{: 1}=\operatorname{Softmax}\left(\mathbf{K}^{T} \mathbf{q}_{: 1}\right) \in \mathbb{R}^{m} α:1=Softmax(KTq:1)∈Rm
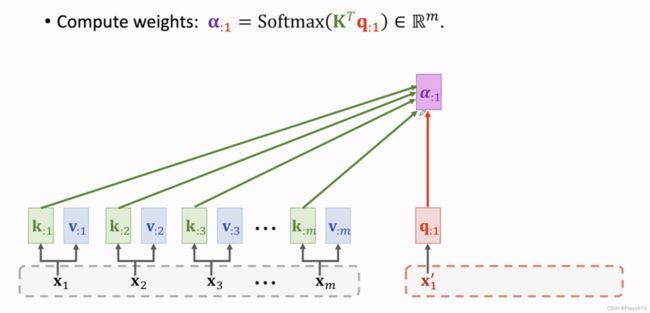
然后计算context向量 c : 1 c_{: 1} c:1,需要用到权重向量 α : 1 \alpha_{: 1} α:1以及所有 v : m v_{: m} v:m。 c : 1 c_{: 1} c:1就是m个v向量的加权平均。
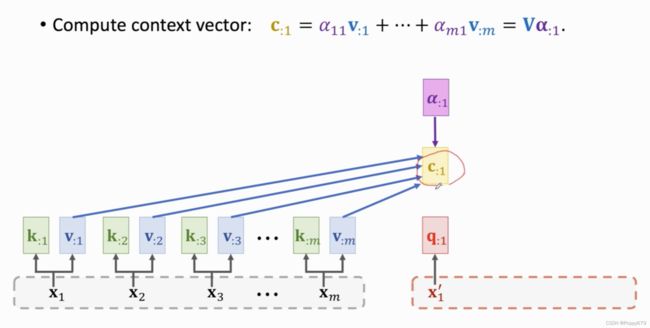
第二个权重向量和context向量和之前计算方式相同,由此就可以计算出所有context向量 c : j c_{: j} c:j。每个c对应一个decoder的输入 x ′ x' x′。decoder中有t个向量,则会计算出t个c值,这些c就是attention layer的输出,用 C C C表示。
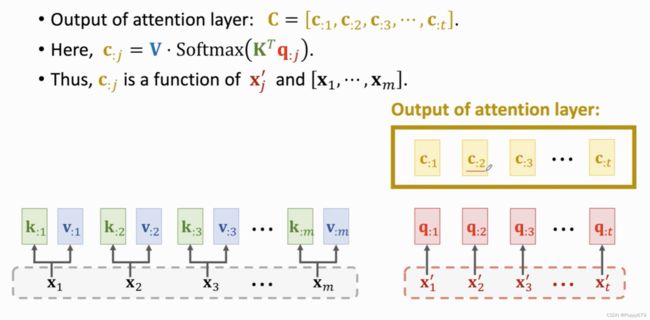
回到之前英语翻译德语的例子,m个英语单词输入encoder,然后由decoder来依次产生德语单词。第2个context向量 c : 2 c_{: 2} c:2可以通过key和value向量看到所有的英语单词,即 x 1 , x 2 , . . . , x m x_1,x_2,...,x_m x1,x2,...,xm,同时还能看到 x 2 ′ x'_2 x2′,即当前输入的德语单词。此时可以将 c 2 c_2 c2作为一个特征向量输入到softmax分类器,来计算概率分布 p 2 p_2 p2,然后通过 p 2 p_2 p2抽样得出第三个德语单词,编码成 x 3 ′ x'_3 x3′,作为下一轮的输入(decoder)。
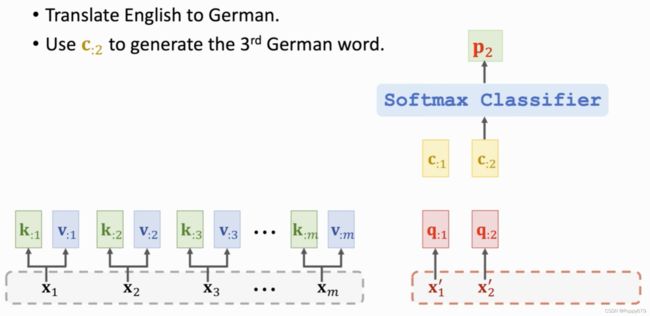 attention layer替代RNN,优势:不会遗忘。attention层的输入是 X X X和 X ′ X' X′,输出是 c 1 , c 2 , . . . , c t c_1,c_2,...,c_t c1,c2,...,ct,每一个 c c c向量对应一个 x ′ x' x′向量.
attention layer替代RNN,优势:不会遗忘。attention层的输入是 X X X和 X ′ X' X′,输出是 c 1 , c 2 , . . . , c t c_1,c_2,...,c_t c1,c2,...,ct,每一个 c c c向量对应一个 x ′ x' x′向量.
Self-attention without RNN
Attention层用于Seq2Seq有两个输入序列。Self-Attention不是seq2seq,只有一个输入序列。类似普通RNN。self-attention层的输入是两个相同的 X X X序列,一个 c c c向量都对应一个 x x x向量,但 c i c_i ci不止依赖于 x i x_i xi,而是依赖所有 x x x向量,改变其中任何 x x x, c i c_i ci都会发生变化。
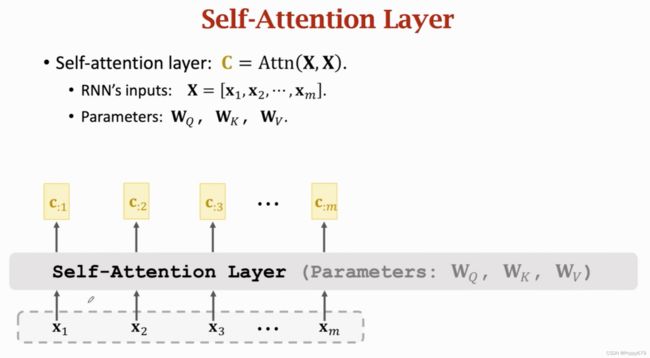
self-attention层的原理和attention层的原理完全一样,只是输入不一样。self-attention只有一个输入序列 x 1 , x 2 , . . . , x m x_1,x_2,...,x_m x1,x2,...,xm。
计算过程
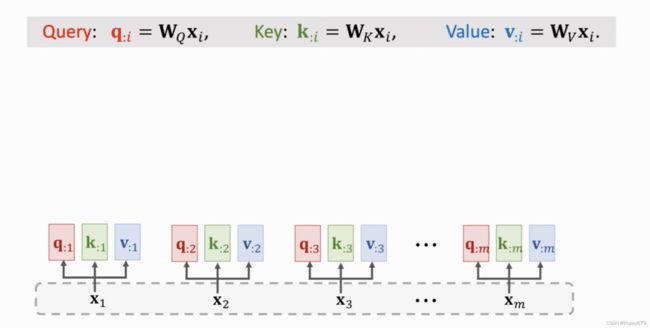
第一步是做三种变换:将 x i x_i xi映射到三种向量 q : i , k : i , v : i q_{: i},k_{: i},v_{: i} q:i,k:i,v:i上。参数依然是 W Q , W K , W V W_Q,W_K,W_V WQ,WK,WV。线性变换后, x 1 x_1 x1映射到 q : 1 , k : 1 , v : 1 q_{:1},k_{: 1},v_{: 1} q:1,k:1,v:1,其余类似。
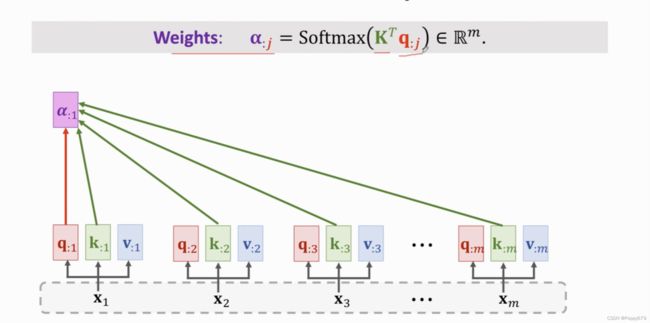
第二步计算权重向量 α \alpha α。权重 α : j \alpha_{: j} α:j依赖于相应的 q : j q_{: j} q:j和所有 k k k。利用公式计算出所有的权重向量: α : j = Softmax ( K T q : j ) ∈ R m \boldsymbol{\alpha}_{: j}=\operatorname{Softmax}\left(\mathbf{K}^{T} \mathbf{q}_{: j}\right) \in \mathbb{R}^{m} α:j=Softmax(KTq:j)∈Rm,每一个权重向量都是m维的。
第三步计算context向量。对所有 v : j v_{: j} v:j做加权平均去计算相应的 c c c,权重都是 α \alpha α。 c 1 c_1 c1依赖与权重向量 α : 1 \alpha_{: 1} α:1以及所有v向量。同样的方法计算其余c向量
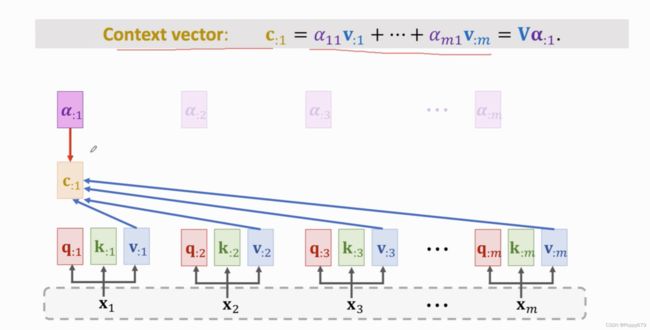
得到的 c : j c_{: j} c:j是self-attention layer的输出。
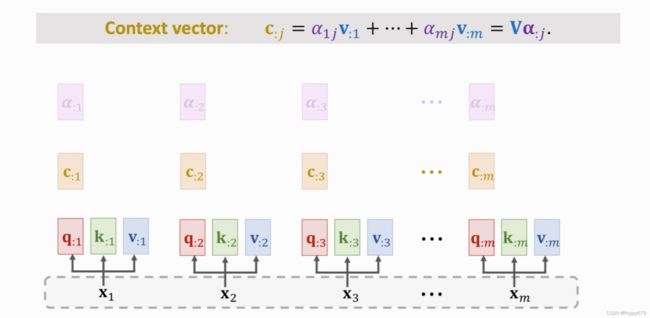
第j个输出 c : j c_{: j} c:j是依赖于矩阵 V V V,矩阵 K K K,和向量 q : j q_{: j} q:j。 c : j c_{: j} c:j依赖m个x向量。

attebtion layer的输入是encoder和decoder的元素,是两个不同的矩阵.输出的长度与decoder的输入长度相同。
self-attention layer的输入是两个相同的矩阵
