五分钟掌握AB实验和样本量计算原理

AB实验简介

什么是AB实验

将测试对象随机分成A,B两组，然后比较两组之间的差异
AB测试是为Web或App界面或流程制作两个（A/B）版本，在同一时间维度，分别让组成成分相同（相似）的访客群组（目标人群）随机的访问这些版本，收集各群组的用户体验数据和业务数据，最后分析、评估出最好版本，正式采用。

需要满足的条件：
对照组：有其他对照组作为对比，就能真正看出来效果。而且不同组间的效果差异要足够明显，才能验证我们的判断
随机性：为了排除实验条件以外的干扰因素，我们需要确保两个组的用户是随机选取，这是为了排除用户差异对实验结果的影响
大样本：这里的样本量是指数据量，包括用户、行为和时间跨度，样本量越大，越容易排除个体差异的影响，也更容易验证统计上的显著性

AB实验的原则

唯一变量：
AB实验时需要保证除了要实验的变量之外，实验组和对照组其他的“变量”都是均匀的，包含但不限于：
时间、环境、样本属性等
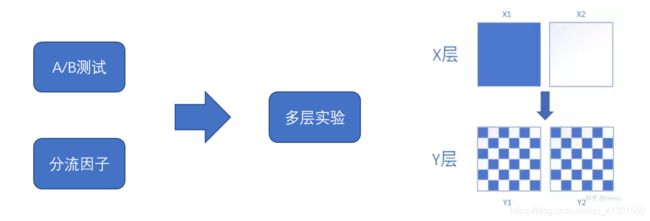
多层实验如何保证唯一变量：
分流因子通过加入不同的字符串（实验名）作为离散因子，保证每层都是正交分布，防止层与层之间有交集。

AB实验涉及的统计学基础

抽样

实验的思想：
用能近似代表总体的样本推断总体的分布(假设检验)，利用样本指标近似代替总体指标，继而进行决策；
如何保证：
近似代表总体的样本需满足以下2项条件：
1、随机抽样：实验中的样本是随机抽取的。而且抽取的算法能够充分保证了抽样的随机性。
2、样本能近似代表总体：
样本量越大，通过样本去评估总体的误差就越小。当误差小于我们需要的精度时样本量就足够了。
$$\begin{gathered} E(\bar{X})=E(1/n\sum _{i=1}^n{X}_i)=\frac{1}{n}\sum _{i=1}^{n}E(X_i)=\mu \\ D(\bar{X})=D(1/n\sum _{i=1}^n{X}_i)=\frac{1}{n^2}\sum _{i=1}^{n}D(X_i)=\frac{1}{n}{\sigma }^2 \end{gathered}$$
所以当n较大时， $\bar{X}$近似服从$N(\mu ,\frac{{\sigma }^2}{n})$，等价地有$\frac{\bar{X}-\mu }{\sigma /\sqrt{n}}\sim N(0,1)$。
中心极限定理（central limit theorem）：设均值为$\mu$、方差为${\sigma }^2$（有限）的任意一个总体中抽取样本量为n的样本，当n充分大时，样本均值$\mu$的抽样分布近似服从均值为$\mu$、方差为 $\frac{1}{n}{\sigma }^2$的正态分布。

样本量计算

样本量计算公式：
均值检验样本量预估：$n=\frac{(Z_{1-\alpha /2}+Z_{1-\beta }){\sigma }^2}{E^2}$

率值检验样本量预估：$n=\frac{(Z_{1-\alpha /2}+Z_{1-\beta })\pi (1-\pi )}{E^2}$
公式中的E代表假设实验能够带来的指标变化值。

要想知道样本量计算公式具体是怎么来的，首先要了解假设检验中的两类错误：

第一类错误代表的是原假设成立，但是却拒绝了原假设的概率，也即上图中阴影面积$\alpha$;
第二类错误代表的是备择假设成立，当检验指标落在原假设的接受域时，在备择假设下的概率，也即上图中阴影面积$\beta$，通俗点说就是，给定第一类错误$\alpha$下，备择假设中的样本，在原假设下检验时接受原假设的可能性。
检验功效是指正确拒绝原假设的概率，也即备择假设成立时，检验拒绝原假设的概率，在数值上和第二类错误有以下数量关系：
$$Power=1-\beta$$
下面我们来推导样本量的计算公式：

首先从单变量假设开始推导

原假设：$H_0:\mu =0$
备择假设：$H_1:\mu <>0(\mu ={\mu }_1)$

给定样本均值$\bar{X}$，一类错误$\alpha$，二类错误$\beta$，令$Z=\frac{\bar{X}-\mu }{\sigma /\sqrt{n}}$
则：
$$P(|Z|\ge Z_{1-\alpha /2})=\alpha \Rightarrow |Z|=|\frac{\bar{X}-\mu }{\sigma /\sqrt{n}}|\ge Z_{1-\alpha /2}\Rightarrow |\bar{X}|\ge Z_{1-\alpha /2}\frac{\sigma }{\sqrt{n}}$$
意味着$|\bar{X}|\ge Z_{1-\alpha /2}\frac{\sigma }{\sqrt{n}}$时，可以拒绝原假设。
但同时需要保证第二类错误，则当$\bar{X}\sim N({\mu }_1,\frac{{\sigma }^2}{n})$时，假设${\mu }_1>0$，则要求单边检验
$$P(\bar{X}\ge Z_{1-\alpha /2}\frac{\sigma }{\sqrt{n}}{)}_{\bar{X}\sim N({\mu }_1,\frac{{\sigma }^2}{n})}\ge 1-\beta$$
同时对$\bar{X}$进行标准化，可以得到
$$P(\frac{\bar{X}-{\mu }_1}{\sigma /\sqrt{n}}\ge \frac{Z_{1-\alpha /2}\frac{\sigma }{\sqrt{n}}-{\mu }_1}{\sigma /\sqrt{n}})\ge 1-\beta$$
其中$\frac{\bar{X}-{\mu }_1}{\sigma /\sqrt{n}}\sim N(0,1)$，则只需要$\frac{Z_{1-\alpha /2}\frac{\sigma }{\sqrt{n}}-{\mu }_1}{\sigma /\sqrt{n}}\le -Z_{1-\beta }$（各位自行画出正态图像判断），求解方程可以得到：
$$n\ge \frac{{\sigma }^2}{{\mu }_1^2}(Z_{1-\alpha /2}+Z_{1-\beta }{)}^2$$
这里的${\mu }_1$的含义就是预计实验带来的指标变化大小，也即E的值；
在实际应用中可以利用样本方差$S_n^2$代替${\sigma }^2$来计算所需样本量，率值的${\sigma }^2=\pi (1-\pi )$,可以得到
$$n\ge \frac{\pi (1-\pi )}{{\mu }_1^2}(Z_{1-\alpha /2}+Z_{1-\beta }{)}^2$$

接下来重新回归AB实验问题，即两样本均值或率值检验时

假设A组服从分布$N({\mu }_A,{\sigma }^2)$，B组服从分布$N({\mu }_B,{\sigma }^2)$，这两样本均值差$\overline{X_A}-\overline{X_B}$服从$N({\mu }_A-{\mu }_B,{\sigma }^2/(\frac{1}{\frac{1}{n_A}+\frac{1}{n_B}}))$
同时，假设两组的样本量$n_A=k{n}_B$，则可以计算得到
两样本均值检验，最小样本量为
$$n_B\ge (1+\frac{1}{k})\frac{{\sigma }^2}{({\mu }_A-{\mu }_B{)}^2}(Z_{1-\alpha /2}+Z_{1-\beta }{)}^2$$
两样本率值检验，最小样本量位
$$n_B\ge (1+\frac{1}{k})\frac{\pi (1-\pi )}{({\mu }_A-{\mu }_B{)}^2}(Z_{1-\alpha /2}+Z_{1-\beta }{)}^2$$

效果评估（最小重要变化-目标提升值）

在工业运用中，只有当试验版本的结果兼备统计显著和效果显著两个特征时，才说明这个试验的结束时机已经成熟，该版本是真正值得发布的，因此，我们需要引入一个“最小重要变化”的概念来辅助我们判断和决策。


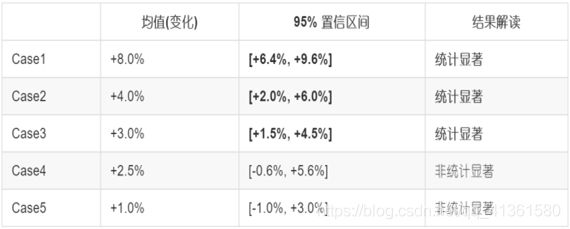
当置信区间的上下上下界都超过或低于最小重要变化时才说他是效果显著的。