动手学深度学习18——模型选择+过拟合和欠拟合及代码实现
一、模型选择
1、怎么选择超参数
例:预测谁会偿还贷款
银行雇你来调查谁会偿还贷款,你得到了100个申请人的信息,其中五个人三年内违约了(换不清贷款),你发现所有的5个人在面试的时候都穿了蓝色衬衫,你的模型也发现了这个强信号,这会有什么问题?
2、训练误差和泛化误差
- 训练误差:模型在训练数据上的误差。
- 泛化误差:模型在新数据上的误差。
例子:根据模考成绩来预测未来考试分数。
在过去的考试中表现很好(训练误差)不代表未来考试一定会好(泛化误差)
3、验证数据集和测试数据集
- 验证数据集:一个用来评估模型好坏的数据集。
例如:拿出50%的训练数据;不要跟训练数据集混在一起。
- 测试数据集:只用一次的数据集
例如:未来的考试;我出价的房子的实际成交价;用在Kaggle私有排行榜中的数据集。
4、k-折交叉验证
在没有足够多的数据时使用(这是常态),算法就是将训练数据集分割成k块,for i=1,.....,K;使用第i块作为验证数据集,其余的作为训练数据集,报告k个验证集误差的平均。(常用k=5或10)
5、总结
训练数据集:训练模型参数。
验证数据集:选择模型超参数。
非大数据集上通常使用k-折交叉验证
二、过拟合和欠拟合
1、模型容量
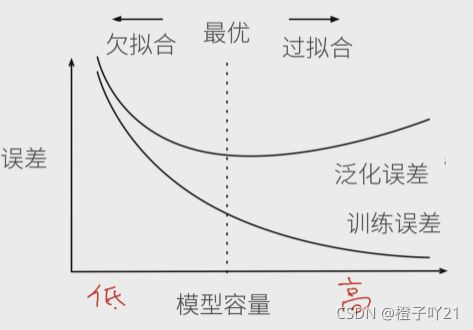
模型容量:就是拟合各种函数的能力。低容量的模型难以拟合训练数据;高容量的模型可以记住所有的训练数据。
模型容量的影响:
估计模型容量
难以在不同的种类算法之间比较,例如树模型和神经模型;
给定一个模型种类,将有两个主要因素:参数的个数和参数值的选择范围。
2、VC维
VC维:统计学习理论的一个核心思想;对于一个分类模型,VC等于一个最大数据集的大小,不管如何给定标号,都存在一个模型来对它进行完美分类。
线性分类器的VC维:2维输入的感知机,VC维=3,能够分类任何三个点,但是不是四个。
支持N维输入的感知机的VC维是N+1;一些多层感知机的VC维O(N* log2 N)
VC维的用处:
提供为什么一个模型好的理论依据,它可以衡量训练误差和泛化误差之间的间隔,但深度学习中很少使用,衡量不是很准确,计算深度学习模型的VC维很困难。
3、数据复杂度
多个重要因素:
- 样本个数;
- 每个样本的元素个数;
- 时间、空间结构;
- 数据的多样性;
4、总结
- 模型容量需要匹配数据复杂度,否则可能导致欠拟合和过拟合;
- 统计机器学习提供数学工具来衡量模型复杂度;
- 实际中一般考观察训练误差和验证误差;
三、代码实现
import matplotlib.pyplot as plt
import torch
import numpy as np
import sys
sys.path.append("..")
import d2lzh_pytorch as d2l
"""
1、生成数据集
"""
n_train, n_test, true_w, true_b = 100, 100, [1.2, -3.4, 5.6], 5
#训练数据集和测试数据集的样本数都设置为100,true_w是权重,true_b是偏差;
features = torch.randn((n_train + n_test, 1))
poly_features = torch.cat((features, torch.pow(features, 2),torch.pow(features, 3)), 1)
labels = (true_w[0] * poly_features[:, 0] + true_w[1] * poly_features[:, 1]+ true_w[2] * poly_features[:, 2] + true_b)
labels += torch.tensor(np.random.normal(0, 0.01,size=labels.size()), dtype=torch.float)
print(features[:2], poly_features[:2], labels[:2])
#输出数据集的前两个样本
"""
2、定义、训练和测试模型
"""
#定义作图函数semilogy,其中y轴使⽤了对数尺度。
def semilogy(x_vals, y_vals, x_label, y_label, x2_vals=None,y2_vals=None,legend=None, figsize=(3.5, 2.5)):
d2l.set_figsize(figsize)
d2l.plt.xlabel(x_label)
d2l.plt.ylabel(y_label)
d2l.plt.semilogy(x_vals, y_vals)
if x2_vals and y2_vals:
d2l.plt.semilogy(x2_vals, y2_vals, linestyle=':')
d2l.plt.legend(legend)
#和线性回归⼀样,多项式函数拟合也使⽤平⽅损失函数。
num_epochs,loss=100,torch.nn.MSELoss()
def fit_and_plot(train_features,test_features,train_labels,test_labels):
net =torch.nn.Linear(train_features.shape[-1],1)
batch_size=min(10,train_labels.shape[0])
dataset=torch.utils.data.TensorDataset(train_features,train_labels)
train_iter=torch.utils.data.DataLoader(dataset,batch_size,shuffle=True)
optimizer = torch.optim.SGD(net.parameters(), lr=0.01)
train_ls, test_ls = [], []
for _ in range(num_epochs):
for X, y in train_iter:
l = loss(net(X), y.view(-1, 1))
optimizer.zero_grad()
l.backward()
optimizer.step()
train_labels = train_labels.view(-1, 1)
test_labels = test_labels.view(-1, 1)
train_ls.append(loss(net(train_features),train_labels).item())
test_ls.append(loss(net(test_features),test_labels).item())
print('final epoch: train loss', train_ls[-1], 'test loss',test_ls[-1])
semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss', range(1, num_epochs + 1), test_ls, ['train', 'test'])
print('weight:', net.weight.data,'\nbias:', net.bias.data)
"""前两个样本的输出结果: 进行输出
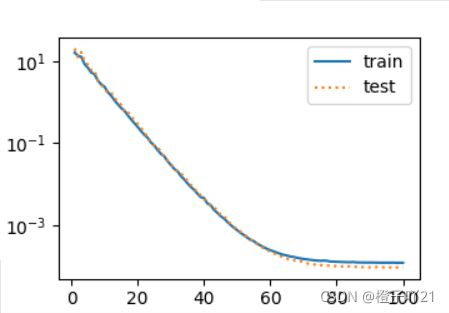
# 三阶多项式函数拟合(正常)
fit_and_plot(poly_features[:n_train, :], poly_features[n_train:, :],labels[:n_train], labels[n_train:])
plt.show()
# 线性函数拟合(⽋拟合)
fit_and_plot(features[:n_train, :], features[n_train:, :],labels[:n_train],labels[n_train:])
plt.show()
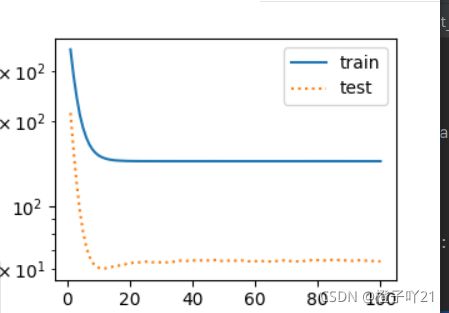
#训练样本不⾜(过拟合)
fit_and_plot(poly_features[0:2, :], poly_features[n_train:, :],labels[0:2],labels[n_train:])
plt.show()
总结:
- 由于⽆法从训练误差估计泛化误差,⼀味地降低训练误差并不意味着泛化误差⼀定会降低。机器 学习模型应关注降低泛化误差。
- 可以使⽤验证数据集来进⾏模型选择。
- ⽋拟合指模型⽆法得到较低的训练误差,过拟合指模型的训练误差远⼩于它在测试数据集上的误差。
- 应选择复杂度合适的模型并避免使⽤过少的训练样本。