深度学习入门：手写体识别

两层神经网络，输入层784个神经元，隐藏层40个，输出层10个。

数据集在这下载：http://yann.lecun.com/exdb/mnist/

数据集中包含60000张训练集图片和标签label，10000张测试集图片和label。每张图片都代表0-9的数字，且为28*28像素。

'''
mnist手写体识别

train_times=2500   learning_rate=0.06    预计用时24min

2020.11.9
'''
import os        #用于数据导入
import struct    #用于数据导入
import numpy as np
import matplotlib.pyplot as plt

'''读取数据'''
def load_mnist(path, kind='train'):
    labels_path = os.path.join(path, '%s-labels.idx1-ubyte' % kind)
    #os.path.join()函数用于路径拼接文件路径
    images_path = os.path.join(path, '%s-images.idx3-ubyte' % kind)
    with open(labels_path, 'rb') as lbpath:
        magic, n = struct.unpack('>II', lbpath.read(8))
        labels = np.fromfile(lbpath, dtype=np.uint8)
    with open(images_path, 'rb') as imgpath:
        magic, num, rows, cols = struct.unpack(">IIII", imgpath.read(16))
        images = np.fromfile(imgpath, dtype=np.uint8).reshape(len(labels), 784)
    return images, labels

'''加载数据'''
x_train, y_train = load_mnist('../DataSet', kind='train')
x_test, y_test = load_mnist('../DataSet', kind='t10k')

'''数据预处理'''
#归一化
x_train = 1.0*x_train.T/255    #size: 784*60000
x_test = 1.0*x_test.T/255      #size: 784*10000
#标签onehot编码
y_train_vector = np.zeros((10, 60000))
y_test_vector = np.zeros((10, 10000))
for i in range(len(y_train)):
    y_train_vector[y_train[i]][i] = 1
for i in range(len(y_test)):
    y_test_vector[y_test[i]][i] = 1


def sigmoid(z):
    '''激活函数'''
    return (1 / (1 + np.exp(-z)))


def Init_paras(pre_layers_dims,next_layers_dims):
    '''参数w,b随机初始化'''
    '''为防止梯度消失和梯度爆炸，w初始化时，乘以一个与上一输入层有关的数值。'''
    w = np.random.randn(pre_layers_dims, next_layers_dims) * np.sqrt(1 / pre_layers_dims)
    b = np.zeros((next_layers_dims,1))
    return  w,b


def forword_pro(w1,b1,w2,b2,x,y_v):
    '''前向传播'''
    z1 = np.dot(w1.T,x) + b1
    a1 = sigmoid(z1)                 # a1 : 40*60000
    z2 = np.dot(w2.T,a1) + b2         #z2:  10*60000
    a2 = np.exp(z2)/np.sum(np.exp(z2),axis=0,keepdims=True)   #softmax a2 : 10*60000
    
    m = x.shape[1]     #m=60000
    J = -1/m * np.sum(np.sum(y_v*np.log(a2),axis = 0))    #成本函数
    return a1,a2,J


def back_pro(a1,a2,w2,x,y_v):
    '''反向传播'''
    m = x.shape[1]     #m=60000

    dz2 = a2 - y_v    #10*60000
    dw2 = 1/m * np.dot(a1,dz2.T)       #40*10
    db2 = 1/m * np.sum(dz2,axis=1,keepdims=True)   #10*1

    da1 = np.dot(w2,dz2)                 #40*60000
    dz1 = da1 * a1 * (1-a1)              #40*60000
    dw1 = 1/m * np.dot(x,dz1.T)                #784*40
    db1 = 1/m * np.sum(dz1,axis=1,keepdims=True)   #40*1

    return dw1,db1,dw2,db2


def predict(w1,b1,w2,b2,x,y,y_v):
    '''准确率预测'''
    m = x.shape[1]      #60000
    y_predict = np.zeros((m,1))     #60000*1
    #前向预测
    a1,a2,J = forword_pro(w1,b1,w2,b2,x,y_v)    #a2: 10*60000

    #确保矩阵维数正确
    y = y.reshape(-1,1)  #将维度从(60000,) 转为(60000,1)
    a2_list = list(a2.T)
    
    for i in range(m):     #预测结果以单个数字表示
        y_predict[i] = list(a2_list[i]).index(max(a2_list[i]))
        
    right_num =np.count_nonzero((y_predict-y)==0) 
    accuracy = right_num / m
    
    return a1,a2,J,accuracy,y_predict


def gradient_des(w1,b1,w2,b2,x,y,y_v,t_t,l_r):
    '''梯度下降,得到训练后的w,b'''
    '''记录每次更新参数后的损失函数和准确率'''
    J_set = []
    accuracy_set = []
    
    for i in range(t_t):
        
        a1,a2,J,accu,pre = predict(w1,b1,w2,b2,x,y,y_v) #前向传播+准确率预测
        J_set.append(J)              #记录损失函数
        accuracy_set.append(accu)    #记录准确率
        
        '''更新参数'''
        dw1,db1,dw2,db2 = back_pro(a1,a2,w2,x,y_v)     #反向传播
        w1 = w1 - l_r * dw1                            #更新参数
        b1 = b1 - l_r * db1
        w2 = w2 - l_r * dw2
        b2 = b2 - l_r * db2

        if i % 100 == 0:
            print(i,'times cost:','%.7f' % J,'accuracy:','%.2f' % (accu*100),'%')
            
    return w1,b1,w2,b2,J_set,accuracy_set


def model(x_train, y_train, y_train_vector, x_test, y_test, y_test_vector, train_times, learning_rate):
    #随机初始化参数
    w1,b1 = Init_paras(x_train.shape[0],40)    # w1 : 784*40      b1 : 40*1
    w2,b2 = Init_paras(40,10)                  # w2 : 40*10       b2 : 10*1

    #梯度下降训练
    w1,b1,w2,b2,cost,accuracy_set = gradient_des(w1,b1,w2,b2,x_train,y_train,y_train_vector,train_times,learning_rate)

    #训练后测试结果
    train_pre = predict(w1,b1,w2,b2,x_train,y_train,y_train_vector)
    test_pre = predict(w1,b1,w2,b2,x_test,y_test,y_test_vector)

    #输出效果
    print('训练集准确率:', '%.2f' % (train_pre[3]*100),'%')
    print('测试集准确率:', '%.2f' % (test_pre[3]*100),'%')

    return cost,accuracy_set,train_pre[4],test_pre[4]


cost,accuracy,train_pre,test_pre = model(x_train,y_train,y_train_vector,x_test,y_test,y_test_vector,2500,0.02)
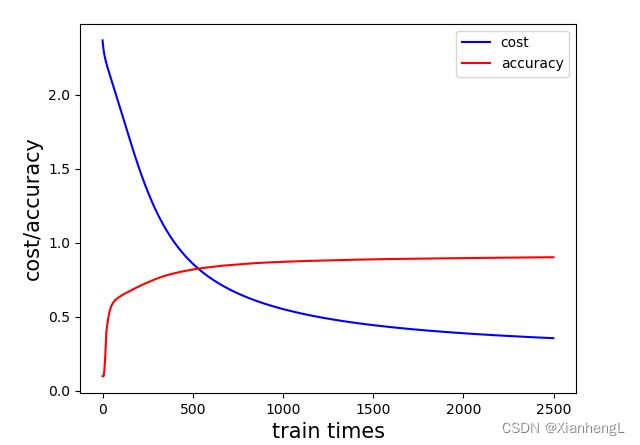
plt.plot(cost,'b',accuracy,'r')
plt.xlabel('train times', fontsize=15)
plt.ylabel('cost/accuracy', fontsize=15)
plt.legend(labels = ['cost', 'accuracy'], loc = 'best')
plt.show()

训练过程：

train_times=2500
learning_rate=0.06
训练预计用时24min

0 times cost: 2.3682727 accuracy: 9.87 %
100 times cost: 1.9012141 accuracy: 64.04 %
200 times cost: 1.5136139 accuracy: 70.53 %
300 times cost: 1.2088581 accuracy: 75.85 %
400 times cost: 1.0007057 accuracy: 79.55 %
500 times cost: 0.8599982 accuracy: 82.09 %
600 times cost: 0.7611588 accuracy: 83.77 %
700 times cost: 0.6884455 accuracy: 84.99 %
800 times cost: 0.6327767 accuracy: 85.95 %
900 times cost: 0.5887952 accuracy: 86.71 %
1000 times cost: 0.5531865 accuracy: 87.23 %
1100 times cost: 0.5237943 accuracy: 87.71 %
1200 times cost: 0.4991503 accuracy: 88.08 %
1300 times cost: 0.4782147 accuracy: 88.40 %
1400 times cost: 0.4602264 accuracy: 88.66 %
1500 times cost: 0.4446144 accuracy: 88.91 %
1600 times cost: 0.4309409 accuracy: 89.13 %
1700 times cost: 0.4188654 accuracy: 89.31 %
1800 times cost: 0.4081191 accuracy: 89.47 %
1900 times cost: 0.3984880 accuracy: 89.62 %
2000 times cost: 0.3897997 accuracy: 89.75 %
2100 times cost: 0.3819146 accuracy: 89.87 %
2200 times cost: 0.3747182 accuracy: 90.00 %
2300 times cost: 0.3681163 accuracy: 90.11 %
2400 times cost: 0.3620307 accuracy: 90.23 %
训练集准确率: 90.33 %
测试集准确率: 90.78 %

用训练好的模型测试：

# -*- coding: utf-8 -*-
"""
Created on Mon Dec  7 20:57:13 2020

@author: 26676
"""
import numpy as np
from PIL import Image

def sigmoid(z):
    '''激活函数'''
    return (1 / (1 + np.exp(-z)))

def number_recognize(w1, b1, w2, b2, x):
    z1 = np.dot(w1.T, x) + b1
    a1 = sigmoid(z1)                 # a1 : 40*60000
    z2 = np.dot(w2.T, a1) + b2         #z2:  10*60000
    a2 = np.exp(z2)/np.sum(np.exp(z2), axis=0, keepdims=True)   #softmax a2 : 10*60000
    a2_list = list(a2.T)
    result = list(a2_list[0]).index(max(a2_list[0]))
    return result, a2
'''读取图像'''
img = Image.open('F:/Python/deeplearn/mnist/test_data/4.jpg')
img = img.convert('L')  #转为灰度图像
img = img.resize((28, 28), Image.ANTIALIAS)  #修改像素大小为28*28
img.save('F:/Python/deeplearn/mnist/test_data_gray/4.jpg')
img_num = np.array(img)
x = img_num.reshape(img_num.shape[0]*img_num.shape[1], 1)  #将像素铺平
x = 1.0 * x / 255    #归一化
print(x.shape)
'''读取训练好的w和b'''
w1 = np.load('F:/Python/deeplearn/mnist/result/w1.npy')
w2 = np.load('F:/Python/deeplearn/mnist/result/w2.npy')
b1 = np.load('F:/Python/deeplearn/mnist/result/b1.npy')
b2 = np.load('F:/Python/deeplearn/mnist/result/b2.npy')

number, a = number_recognize(w1, b1, w2, b2, x)
print(number)