复指数与高斯函数乘积的傅里叶变换_希尔伯特变换:将实数信号变换成解析信号?节省带宽,提升效率...
通信中的调制,我们可以看作为在频域范围内的频谱搬移技术。
对于一个原始信号m(t),我们加上一个直流分量A0,再乘以载波信号,就得到了调幅AM信号。
AM信号,之前的文章介绍过。
模拟调制:我们为什么要调制?先从AM幅度调制开始
对于AM信号,其时域与频域的变化过程如图1所示。原始信号m(t)加上一个直流分量A0,然后再与载波相乘,得到已调信号Sam(t);与之对应的,原始信号m(t)的频谱为M(ω),经过载波调制后,已调信号Sam(t)的频谱出现了搬移。
DSB信号
AM信号中,加一个直流分量A0。由"典型信号傅里叶变换"可知,直流分量的傅里叶变换为冲激函数,所以图1中,可以在频域中看到冲激(红色箭头)
为什么要加上一个直流分量?
这个直流分量的累加(需要满足一定的条件),是保证已调制信号的包络与原始信号m(t)保持一致。然后通过简易的包络检波器进行检波。
现在我们把直流分量去掉,如图3所示
此时已调信号Sdsb(t)的包络已经不再与m(t)保持一致了,所以此时不能用包络解调器,而需要用相干解调器。
相干解调:三角函数公式有何用?原来就是通信中的调制解调过程
时域表达式可以写作
频域表达式为
截止目前,我们所说的基带信号频谱均是关于纵坐标轴(零点)对称的,因此会出现负频率。负频率只有数学上的意义,并不实际占用带宽。但是基带信号调制到高频之后,形成了关于Wc的对称频谱,原来的负频率是占用了实实在在的频率资源的。
我们把这种信号叫作双边带信号DSB(Double Side Band),Wc左边的边带叫下边带,Wc右边的边带叫上边带。我们在接收端,通过一些滤波操作,获取这些频谱信息,然后恢复出原始信号。
很明显,我们希望占用少量的带宽,就可以恢复出原来的信号。
因为频谱资源非常稀缺,在同一个频率段,如果张三用了,李四就不能用了,会造成相互间干扰!
双边带信号占用了两倍的频率资源,造成了浪费。
|那怎么办呢?最直接的办法就是把基带信号的频谱砍掉一半|
SSB信号
用阶跃函数可以实现这个目的,图像为
用两倍的阶跃函数与基带信号的频谱相乘,得到基带信号的单边带信号(SSB,Single Side Band)的频谱,
2倍因子是为了使信号的形式更简单(还有一层原因,是引入负频率后,原先正频率的幅度值降低一半,这里把负频率削去,自然要补上这一半)。调制到射频后,得到射频的单边带频谱,如图6所示。
上下边带的频谱是对称的,我们只要知道一个边带,其他的信息自然就知道了。
Hilbert变换
图6已经清楚的描述了M(w)被"削"去一半边带的过程。那么其时域的情况呢?
根据傅里叶变换的性质,频域相乘对应时域卷积,我们得到
根据之前班长与大家所述的内容,阶跃函数的傅里叶变换为
那么根据傅里叶变换的对称与尺度特性
最终可以得出频域阶跃函数的时域表达式。
那么,
我们做一个定义
可以认为信号s(t)经过一个系统后的响应,系统的冲激响应为h(t)=1/πt。
在零点处,可以认为h(t)=0,如图8所示。这个系统有一个专门的名字叫作希尔伯特变换。
没错,我们在推导SSB信号的时域表达式时,不小心"发现"了希尔波特变换。
频域表达式可以写成
频域乘积,时域卷积,可以得出
根据两种不同的表达形式,我么可以得出希尔伯特变换的频域特性:
也可以直接通过冲激响应h(t)=1/πt,取傅里叶变换得出。这个积分需要一定技巧。
我们知道引入虚数j,可以更加方便的表达旋转。
所以从频域响应可以看出,希尔伯特变换不会改变幅度值,对于正频率w>0,相移-90度;对于负频率w<0,相移+90度;
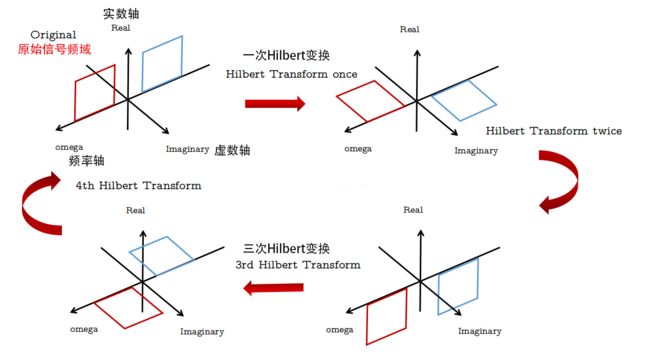
图8描述了对信号进行4次希尔伯特变换,频域的变化过程。每一次在时域进行希尔伯特变换,那么在频域就出现一次90度相位翻转。二次希尔伯特变换后,得到了原频域信号的相;四次希尔伯特变换后,恢复原频域信号。
|希尔伯特的逆变换|
很明显,如果我知道一个信号的希尔伯特变换,那么我们再对他进行一次希尔伯特变换,然后再求傅里叶反变换,就可以得到原始的时域信号了。
总结
到这里,我们知道对于一个双边带信号m(t),只需要加上自身的希尔伯特变换,就可以得到单边带信号SSB了,
此时,节省了一半带宽。
更为一般的,实数信号x(t),Hilbert变换信号为x~(t),那么把两者相加,
得到的信号我们叫做解析信号。
有SSB推导过程看出,解析信号的频谱只有正频段且幅度值为原来的两倍,实现了信号由双边谱转换成单边谱。
将实数信号变换成解析信号的结果就是,把一个一维的信号变成了二维复平面上的信号,复数的模和幅角代表了信号的幅度和相位,如图9所示。
欧拉公式表明,复指数信号e^jx可以表示成一个实数信号和一个虚数信号的和的形式,看着和解析信号是多么的相似啊!
欧拉公式实际上是一种特殊的,或者说,最简单的Hilbert变换。
@通信M班长