聚类算法学习——kernel K-means及实现过程

聚类算法学习

接着上一个博客的学习，这篇对改进算法kernel K-means进行了整理记录。

---

**第二节 核空间聚类学习**

---

前言

物以类聚，人以群分。
以下为学习笔记整理

---

一、kernel是什么？

相信刚接触核空间思想的小伙伴，在搜索帖子学习的过程中，脑海里不止一次会想到“Kernel is a shit！！！”，但是但是但是，核空间太厉害了好吗，它确确实实是低维空间映射到高维的核武器。

“kernel方法是一类用于模式分析或识别的算法，其最知名的使用是在支持向量机（SVM）。模式分析的一般任务是在一般类型的数据（例如序列，文本文档，点集，向量，图像等）中找到并研究一般类型的关系（例如聚类，排名，主成分，相关性，分类）图表等）。内核方法将数据映射到更高维的空间，希望在这个更高维的空间中，数据可以变得更容易分离或更好的结构化。对这种映射的形式也没有约束，这甚至可能导致无限维空间。然而，这种映射函数几乎不需要计算的，所以可以说成是在低维空间计算高维空间内积的一个工具。”------一段高大上的介绍。
下面通俗的讲一下什么是kernel：

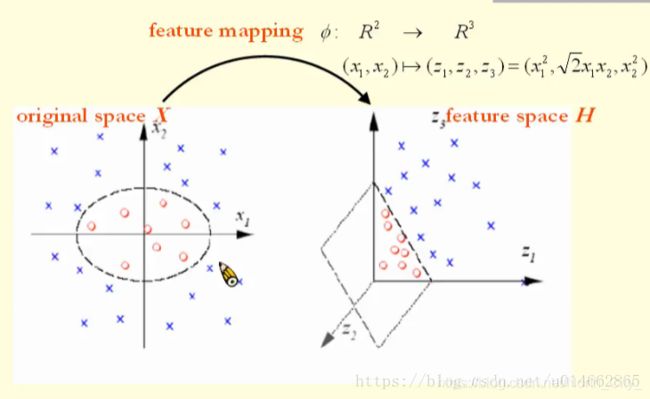
如图所示，左面的图为为原空间，右面的图为映射后的空间，从图中可以看出来，左面图不能线性分割，而右面的图要用一个超平面就可以分割开，原空间点左边为（x1,x2）,经过某个函数或者某种计算方法，转化为特征空间上点坐标为(z1,z2,z3)，所以说将低维空间转化到高维空间大概率可以对其中的点进行线性分割。

这样，我们第一步就理解了，就是在低维空间上的点通过某一函数转化为高维空间上，更有助于线性分类。

映射关系通常不好找，因此借助核函数来避免这个映射关系。上图所使用的核函数为

即内积平方，为什么对应的映射是这样呢，这里可以验证：

目前我还是存在一些困惑，有待进一步理解学习。
首先核函数的选取非常的困难，所举的例子由于数据的特殊性，较容易选择对应的核函数。
在机器学习中常用的核函数，一般有这么几类，也就是LibSVM中自带的这几类：

1）线性：

2）多项式：

3）Radial basis function(RBF径向基函数)：

4）Sigmoid：

更多关于核函数的整理可以参见
https://www.cnblogs.com/infinite-h/p/10723853.html
更详细关于内积解释可以参见
https://www.cnblogs.com/damin1909/p/12955240.html

二、核聚类学习

1.问题描述

首先生成上述图片类似的线性不可分的人工数据集

更新了比前一个更方便的K-means算法（可以实现三维聚类和效果显示）

核函数分别实现了多项式核和高斯核

关于高斯核的解释强烈推荐这篇博客：
https://blog.csdn.net/weixin_42137700/article/details/86756365

2.代码实现

(完整源码可评论我分享）

首先生成人工数据集

def get_data():
    fig = plt.figure()
    x, y1 = make_circles(n_samples=100, factor=0.1, noise=0.1)
    plt.scatter(x[:, 0], x[:, 1], marker='o', c=y1)
    plt.show()

    return x

然后低维空间到高维空间的映射函数

def process(x):
    '''
    映射到高维核空间
    :param data_point:
    :param data_noise:
    :return:
    '''
    Z = np.zeros([100, 3])
    # 二项式映射
    # X[:,0] = _x[:,0]**2
    # X[:, 1] = math.sqrt(2)*_x[:,0]*_x[:,1]
    # X[:,2] = _x[:,1]**2
    
    # 高斯核映射
    Z[:, 0] = np.exp(-(_x[:, 0] ** 2)) * np.exp(-(_x[:, 1] ** 2))
    Z[:, 1] = 2 * _x[:, 0] * _x[:, 1] * np.exp(-(_x[:, 0] ** 2)) * np.exp(-(_x[:, 1] ** 2))
    Z[:, 2] = 2 * _x[:, 0] ** 2 * _x[:, 1] ** 2 * np.exp(-(_x[:, 0] ** 2)) * np.exp(-(_x[:, 1] ** 2))

    return Z

计算空间欧氏距离的函数

def euclidean_distance(one_sample, X):
    one_sample = one_sample.reshape(1, -1)
    X = X.reshape(X.shape[0], -1)
    distances = np.power(np.tile(one_sample, (X.shape[0], 1)) - X, 2).sum(axis=1)

    return distances

更新后的K-means聚类算法

class Kmeans():
    def __init__(self, k=2, max_iterations=500, varepsilon=0.0001):
        self.k = k
        self.max_iterations = max_iterations
        self.varepsilon = varepsilon

    # 从所有样本中随机选取self.k样本作为初始的聚类中心
    def init_random_centroids(self, X):
        n_samples, n_features = np.shape(X)
        centroids = np.zeros((self.k, n_features))
        for i in range(self.k):
            centroid = X[np.random.choice(range(n_samples))]
            centroids[i] = centroid
        return centroids

    # 返回距离该样本最近的一个中心索引[0, self.k)
    def _closest_centroid(self, sample, centroids):
        distances = euclidean_distance(sample, centroids)
        closest_i = np.argmin(distances)
        return closest_i

    # 将所有样本进行归类，归类规则就是将该样本归类到与其最近的中心
    def create_clusters(self, centroids, X):
        n_samples = np.shape(X)[0]
        clusters = [[] for _ in range(self.k)]
        for sample_i, sample in enumerate(X):
            centroid_i = self._closest_centroid(sample, centroids)
            clusters[centroid_i].append(sample_i)
        return clusters

    # 对中心进行更新
    def update_centroids(self, clusters, X):
        n_features = np.shape(X)[1]
        centroids = np.zeros((self.k, n_features))
        for i, cluster in enumerate(clusters):
            centroid = np.mean(X[cluster], axis=0)
            centroids[i] = centroid
        return centroids

    # 将所有样本进行归类，其所在的类别的索引就是其类别标签
    def get_cluster_labels(self, clusters, X):
        y_pred = np.zeros(np.shape(X)[0])
        for cluster_i, cluster in enumerate(clusters):
            for sample_i in cluster:
                y_pred[sample_i] = cluster_i
        return y_pred

    # 对整个数据集X进行Kmeans聚类，返回其聚类的标签
    def predict(self, X):
        # 从所有样本中随机选取self.k样本作为初始的聚类中心
        centroids = self.init_random_centroids(X)

        # 迭代，直到算法收敛(上一次的聚类中心和这一次的聚类中心几乎重合)或者达到最大迭代次数
        for _ in range(self.max_iterations):
            # 将所有进行归类，归类规则就是将该样本归类到与其最近的中心
            clusters = self.create_clusters(centroids, X)
            former_centroids = centroids

            # 计算新的聚类中心
            centroids = self.update_centroids(clusters, X)

            # 如果聚类中心几乎没有变化，说明算法已经收敛，退出迭代
            diff = centroids - former_centroids
            if diff.any() < self.varepsilon:
                break

        return self.get_cluster_labels(clusters, X)

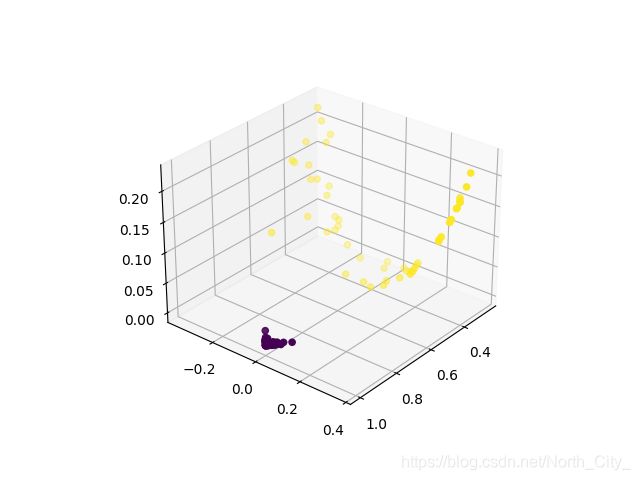
3.结果展示

在高维特征空间聚类成功。

---

总结

这篇文章就先写到这里。下一次整理关于聚类效果的衡量标准。
祝大家都能写Pythonic，少写Cython