NNDL 作业10：第六章课后题（LSTM | GRU）

目录

习题6-3 当使用公式(6.50)作为循环神经网络得状态更新公式时，分析其可能存在梯度爆炸的原因并给出解决办法.

习题6-4 推导LSTM网络中参数的梯度，并分析其避免梯度消失的效果​编辑

习题6-5 推导GRU网络中参数的梯度，并分析其避免梯度消失的效果​编辑

附加题 6-1P 什么时候应该用GRU? 什么时候用LSTM?

附加题 6-2P LSTM BP推导，并用Numpy实现

总结

参考链接

---

习题6-3 当使用公式(6.50)作为循环神经网络得状态更新公式时，分析其可能存在梯度爆炸的原因并给出解决办法.

公式(6.50)为：

再结合上次的BPTT推导：

加上残差连接的反向传播和之前相差不多，以T=2为例，在反向传播时只会多一项，这时会有、、三项。
在《神经网络与深度学习》中将之称为误差项，这一形式和前馈神经网络、普通循环神经网络的误差项形式相同，所以原因都是一样，即在计算误差项时可能会梯度过大从而导致梯度爆炸问题。

解决办法：加入门控机制来控制信息的累计速度，包括有选择地加入新的信息，并有选择地遗忘之前累积的信息。

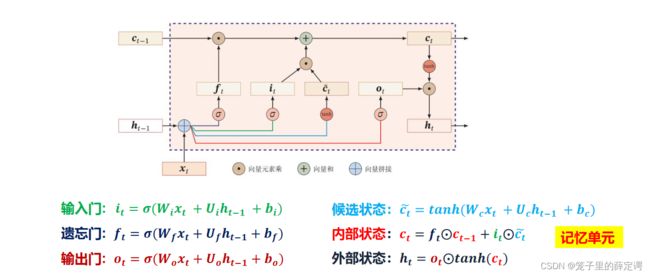
习题6-4 推导LSTM网络中参数的梯度，并分析其避免梯度消失的效果

接下来根据上面的公式，手推梯度：

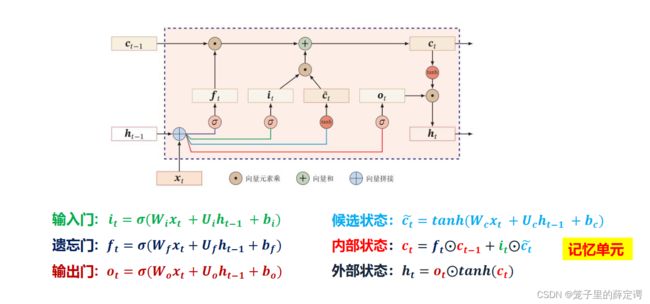
 写的有点乱，其实是不难的，主要就是通过三个门去找上一个时刻的输出，进而通过上一个时刻的输出找上一个时刻的内部状态。

分析其避免梯度消失的效果：
1.观察求导后的四项，可以发现有一个孤零零的遗忘门与另外三个偏导项相加，所以就不太容易趋于0。
2. 从门控机制的理论来看，三个门非0即1。门为0时，上一时刻的信息不会对当前造成影响，进而不会传递更新参数；门为1时，梯度能够很好地在LSTM之间传递，减校了梯度消失发生的概率。

习题6-5 推导GRU网络中参数的梯度，并分析其避免梯度消失的效果

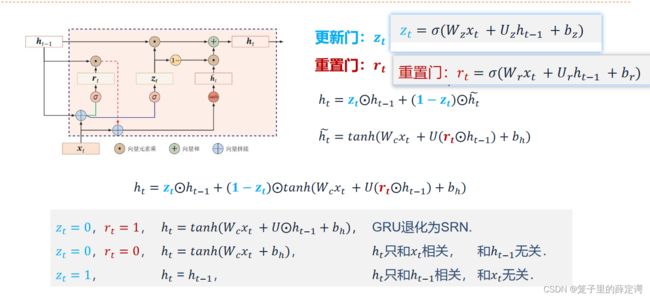
手推一下GRU的反向传播(这个和BPTT的思想很相似，先写出一两项然后总结规律即可，只不过这次我是直接从t时刻反着推的，当然也可以从小时刻开始正着推然后总结规律，都是可行的)：

 和两项的规律和另外四项不太一样，因为涉及到和系数的变动，比较复杂，没有手推，主要就是对GRU的整体思想有一个了解。

避免梯度消失的效果：我觉得效果和LSTM差不多，只不过GRU使用了两个门就近似达到了LSTM三个门的效果。它们都有特殊的方式存储”记忆”，以前梯度比较大的”记忆”不会像简单的RNN一样马上被抹除，因此可以一定程度上克服梯度消失问题。
 

附加题 6-1P 什么时候应该用GRU? 什么时候用LSTM?

在这篇 https://arxiv.org/pdf/1412.3555.pdf 文章中，作者比较了LSTM和GRU的区别，大致意思就是：

1.LSTM通过输出门可以控制整个网络中其他单元看到或使用的记忆单元，而GRU在不加任何控制的情况下向网络中的其他单元公开其全部内容。
2.LSTM可以独立控制加入多少新的“记忆”，与老“记忆”无关，而GRU对新“记忆”的加入会受老“记忆”的约束，老“记忆”留存越多，新“记忆”加入越少。
3.文章的最后验证了两个单元的实验结果相差不多。

我觉得LSTM有三个门控，更加灵活，与之相对应的就是参数量和计算量大，如果对这两项没啥大要求，LSTM可能更好一些？；GRU用两个门效果就能达到LSTM的效果，单元结构简单，因此适合放到大的网络结构里面。

吴恩达老师提到的是：目前为止并没有一个很普适一致的观点，来说明到底哪一个更好，哪一个在哪方面更加适用，大多数人会把LSTM作为默认第一个去尝试的方法。同时GRU，因为其简单而且效果可以（和LSTM）比拟，可以更容易的将其扩展到更大的问题。

所以还是实验为王，具体实验可以把LSTM和GRU单元都试一下，即便没有参数量和计算量的要求，LSTM表现出来的性能也未必好于GRU。

附加题 6-2P LSTM BP推导，并用Numpy实现

有BPTT和前面GRU反向传播的基础(若基础不好，我建议同BPTT一样，从小时刻开始推，进而总结出一般的规律)，推导LSTM的BP挺简单的，如下：

注：第一项在链式求导的时候没有意识到要写成BPTT结果的格式，所以每一小项的最后部分有点问题，需要把最后那一小部分拆成两部分，就可以写成BPTT那样的结果格式(也可以参考第二个参数的计算，第二个参数的推导比较完备)。

代码：

import numpy as np
import torch

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

class LSTMCell:
    def __init__(self, weight_ih, weight_hh, bias_ih, bias_hh):
        self.weight_ih = weight_ih
        self.weight_hh = weight_hh
        self.bias_ih = bias_ih
        self.bias_hh = bias_hh

        self.dc_prev = None
        self.dh_prev = None

        self.weight_ih_grad_stack = []
        self.weight_hh_grad_stack = []
        self.bias_ih_grad_stack = []
        self.bias_hh_grad_stack = []

        self.x_stack = []
        self.dx_list = []
        self.dh_prev_stack = []

        self.h_prev_stack = []
        self.c_prev_stack = []

        self.h_next_stack = []
        self.c_next_stack = []

        self.input_gate_stack = []
        self.forget_gate_stack = []
        self.output_gate_stack = []
        self.cell_memory_stack = []
    def __call__(self, x, h_prev, c_prev):
        a_vector = np.dot(x, self.weight_ih.T) + np.dot(h_prev, self.weight_hh.T)
        a_vector += self.bias_ih + self.bias_hh

        h_size = np.shape(h_prev)[1]
        a_i = a_vector[:, h_size * 0:h_size * 1]
        a_f = a_vector[:, h_size * 1:h_size * 2]
        a_c = a_vector[:, h_size * 2:h_size * 3]
        a_o = a_vector[:, h_size * 3:]

        input_gate = sigmoid(a_i)
        forget_gate = sigmoid(a_f)
        cell_memory = np.tanh(a_c)
        output_gate = sigmoid(a_o)

        c_next = (forget_gate * c_prev) + (input_gate * cell_memory)
        h_next = output_gate * np.tanh(c_next)

        self.x_stack.append(x)

        self.h_prev_stack.append(h_prev)
        self.c_prev_stack.append(c_prev)

        self.c_next_stack.append(c_next)
        self.h_next_stack.append(h_next)

        self.input_gate_stack.append(input_gate)
        self.forget_gate_stack.append(forget_gate)
        self.output_gate_stack.append(output_gate)
        self.cell_memory_stack.append(cell_memory)

        self.dc_prev = np.zeros_like(c_next)
        self.dh_prev = np.zeros_like(h_next)

        return h_next, c_next

    def backward(self, dh_next):
        x_stack = self.x_stack.pop()

        h_prev = self.h_prev_stack.pop()
        c_prev = self.c_prev_stack.pop()

        c_next = self.c_next_stack.pop()

        input_gate = self.input_gate_stack.pop()
        forget_gate = self.forget_gate_stack.pop()
        output_gate = self.output_gate_stack.pop()
        cell_memory = self.cell_memory_stack.pop()

        dh = dh_next + self.dh_prev

        d_tanh_c = dh * output_gate * (1 - np.square(np.tanh(c_next)))
        dc = d_tanh_c + self.dc_prev

        dc_prev = dc * forget_gate
        self.dc_prev = dc_prev

        d_input_gate = dc * cell_memory
        d_forget_gate = dc * c_prev
        d_cell_memory = dc * input_gate

        d_output_gate = dh * np.tanh(c_next)

        d_ai = d_input_gate * input_gate * (1 - input_gate)
        d_af = d_forget_gate * forget_gate * (1 - forget_gate)
        d_ao = d_output_gate * output_gate * (1 - output_gate)
        d_ac = d_cell_memory * (1 - np.square(cell_memory))

        da = np.concatenate((d_ai, d_af, d_ac, d_ao), axis=1)

        dx = np.dot(da, self.weight_ih)
        dh_prev = np.dot(da, self.weight_hh)
        self.dh_prev = dh_prev

        self.dx_list.insert(0, dx)
        self.dh_prev_stack.append(dh_prev)

        self.weight_ih_grad_stack.append(np.dot(da.T, x_stack))
        self.weight_hh_grad_stack.append(np.dot(da.T, h_prev))

        db = np.sum(da, axis=0)
        self.bias_ih_grad_stack.append(db)
        self.bias_hh_grad_stack.append(db)

        return dh_prev


np.random.seed(123)
torch.random.manual_seed(123)
np.set_printoptions(precision=6, suppress=True)

lstm_torch = torch.nn.LSTMCell(2, 3).double()
lstm_numpy = LSTMCell(lstm_torch.weight_ih.data.numpy(),
                      lstm_torch.weight_hh.data.numpy(),
                      lstm_torch.bias_ih.data.numpy(),
                      lstm_torch.bias_hh.data.numpy())

x_numpy = np.random.random((4, 2))
x_torch = torch.tensor(x_numpy, requires_grad=True)

h_numpy = np.random.random((4, 3))
h_torch = torch.tensor(h_numpy, requires_grad=True)

c_numpy = np.random.random((4, 3))
c_torch = torch.tensor(c_numpy, requires_grad=True)

dh_numpy = np.random.random((4, 3))
dh_torch = torch.tensor(dh_numpy, requires_grad=True)

h_numpy, c_numpy = lstm_numpy(x_numpy, h_numpy, c_numpy)
h_torch, c_torch = lstm_torch(x_torch, (h_torch, c_torch))
h_torch.backward(dh_torch)

dh_numpy = lstm_numpy.backward(dh_numpy)

print("h_numpy :\n", h_numpy)
print("h_torch :\n", h_torch.data.numpy())

print("---------------------------------")
print("c_numpy :\n", c_numpy)
print("c_torch :\n", c_torch.data.numpy())

print("---------------------------------")
print("dx_numpy :\n", np.sum(lstm_numpy.dx_list, axis=0))
print("dx_torch :\n", x_torch.grad.data.numpy())

print("---------------------------------")
print("w_ih_grad_numpy :\n",
      np.sum(lstm_numpy.weight_ih_grad_stack, axis=0))
print("w_ih_grad_torch :\n",
      lstm_torch.weight_ih.grad.data.numpy())

print("---------------------------------")
print("w_hh_grad_numpy :\n",
      np.sum(lstm_numpy.weight_hh_grad_stack, axis=0))
print("w_hh_grad_torch :\n",
      lstm_torch.weight_hh.grad.data.numpy())

print("---------------------------------")
print("b_ih_grad_numpy :\n",
      np.sum(lstm_numpy.bias_ih_grad_stack, axis=0))
print("b_ih_grad_torch :\n",
      lstm_torch.bias_ih.grad.data.numpy())

print("---------------------------------")
print("b_hh_grad_numpy :\n",
      np.sum(lstm_numpy.bias_hh_grad_stack, axis=0))
print("b_hh_grad_torch :\n",
      lstm_torch.bias_hh.grad.data.numpy())

运行结果:

总结

这次作业和上次作业关联的很紧密，所有的推导我都是根据上次BPTT的推导步骤，但是貌似结果和老师给的参考结果有点不太一样。我觉得最核心的就是链式求导，静下心来写的会很快。
 

参考链接

NNDL 作业10：第六章课后题（LSTM | GRU）_HBU_David的博客-CSDN博客
Long Short Term Memory (LSTM) - Recurrent Neural Networks | Coursera
GRU和LSTM在各种使用场景应该如何选择？ - 知乎

深度学习算法与编程 (暂停更新)_BrightLampCsdn的博客-CSDN博客

NNDL 作业9：分别使用numpy和pytorch实现BPTT_笼子里的薛定谔的博客-CSDN博客