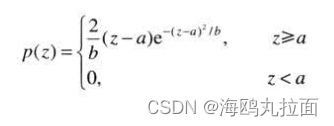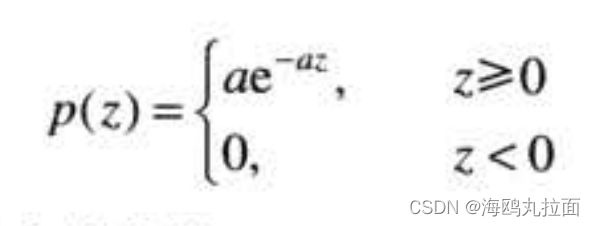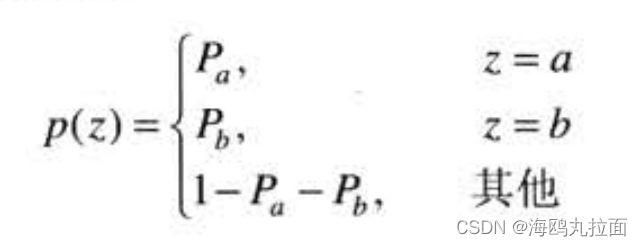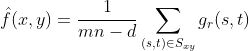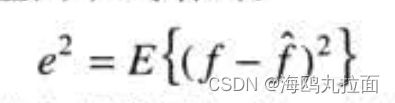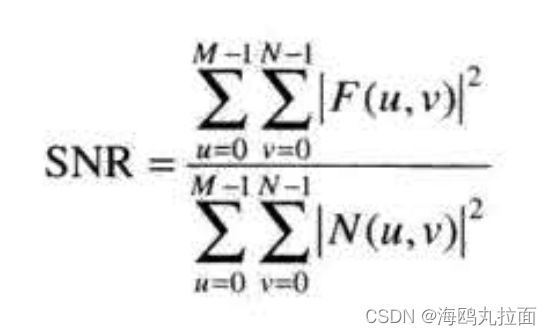数字图像处理第五章——图像复原与重建
目录
5.1 图像退化/复原过程的模型
5.2 噪声模型
5.2.1 噪声的空间和频率特性
5.2.2 一些重要的噪声概率密度函数
高斯噪声
瑞利噪声
爱尔兰（伽马）噪声
指数噪声
均值噪声
脉冲（椒盐）噪声
5.2.3 周期噪声
5.2.4 噪声参数的估计
5.3 只存在噪声的复原——空间滤波
5.3.1 均值滤波器
算数均值滤波器
几何均值滤波器
谐波均值滤波器
逆谐波均值滤波器
5.3.2 统计排序滤波器
中值滤波器
最大值和最小值滤波器
中点滤波器
修正的阿尔法均值滤波器
5.3.3 自适应滤波器
自适应局部降低噪声滤波器
自适应中值滤波器
5.4 用频率域滤波消除周期噪声
5.4.1 带阻滤波器
5.4.2 带通滤波器
5.4.3 陷波滤波器
5.4.4 最佳陷波滤波
5.5 线性、位置不变的退化
可加性
均匀性
5.6 估计退化函数
5.6.1 图像观察估计
5.6.2 试验估计
5.6.3 建模估计
大气湍流模型
运动模糊模型
5.7 逆滤波
5.8 最小均方误差（维纳）滤波
5.9 约束最小二乘方滤波
5.10 几何均值滤波
图像复原技术的主要目的是以预先确定的目标来改善图像，大部分是一个客观的过程。图像复原试图利用退化现象的某种先验知识来复原被退化的图像。因而，复原技术是面向退化模型的，并且采用相反的过程进行处理，以便恢复出原图像。
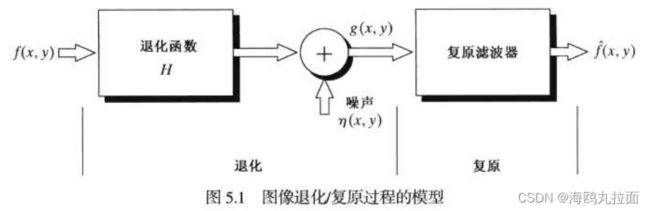
5.1 图像退化/复原过程的模型
如下图所示，退化过程被建模为一个退化函数和一个加性噪声项，对一幅输入图像f(x,y)进行处理，产生一幅退化后的图像g(x,y)。
如果H是一个线性的、位置不变的过程，那么空间域中的退化图像可由下式给出：
等价的频率域表示：
5.2 噪声模型
数字图像中，噪声主要来源于图像的获取和/或传输过程。
5.2.1 噪声的空间和频率特性
频率特性：傅里叶域中噪声的频率内容（即相对于电磁波谱的频率）。
除空间周期噪声外，我们假设噪声与空间坐标无冠，并且噪声与图像本身不相关（即像素值与噪声成分的值之间不相关）。
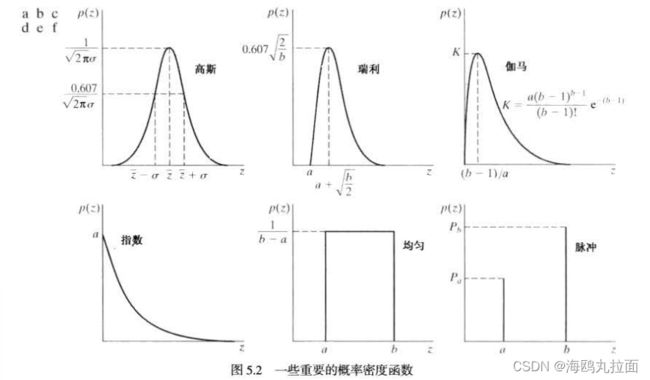
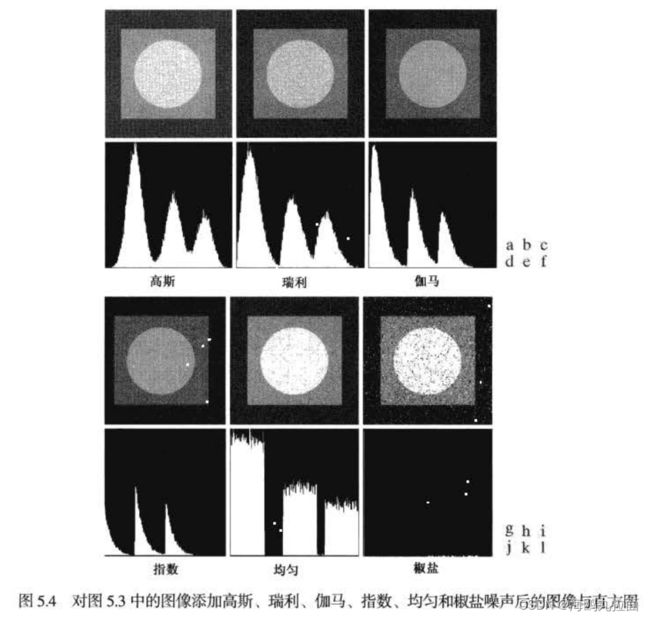
5.2.2 一些重要的噪声概率密度函数
高斯噪声
高斯随机变量z的概率密度函数（PDF）由下式给出：
瑞利噪声
瑞利噪声的PDF由下式给出：
概率密度的均值和方差由
和
爱尔兰（伽马）噪声
概率密度的均值和方差由下式给出：
指数噪声
该概率密度函数的均值和方差是
均值噪声
均值与方差：
脉冲（椒盐）噪声
如果b>a，则灰度级b在图像中将显示为一个亮点；反之，灰度级a在图像中将显示为一个暗点。若Pa或Pb为零，则脉冲噪声称为单机脉冲。如果Pa和Pb两者均不可能为零，尤其是它们近似相等时，则脉冲噪声值将类似于在图像上随机分布的呼叫和椒盐粉粒。
实际上在椒盐噪声中，噪声的值未必都是图像可取值范围中的最大值和最小值。但是与图像信号的强度相比，脉冲污染通常比较大，所以在一幅图像中脉冲噪声通常被数字化为最大值（纯黑或纯白）。
5.2.3 周期噪声
图像中的周期噪声是在图像获取期间由电力或机电干扰产生的。可通过频率滤波器显著减少。
5.2.4 噪声参数的估计
周期噪声的参数通常是通过检测图像的傅里叶谱来估计的。
噪声PDF的参数一般可以从传感器的技术说明中得知，但对于特殊的成像装置通常需要估计这些参数。
当仅有通过传感器生成的图像可用时，通常可由合理的恒定灰度值的一小部分来估计PDF的参数。
5.3 只存在噪声的复原——空间滤波
当一幅图像中唯一存在的退化是噪声时，
噪声项是未知的，故从g(x,y)或G(u,v)中减去它们不显示。在仅存在加性噪声的情况下，可以选择空间滤波的方法进行图像复原。
5.3.1 均值滤波器
算数均值滤波器
是最简单的均值滤波器。令Sxy表示中心在点（x,y）处、大小为mxn的矩形子图像窗口（邻域）的一组坐标。算数均值滤波器在Sxy定义的区域中计算被污染图像g(x,y)的平均值。在点(x,y)处复原图像
的值，就是简单地使用Sxy定义的区域中的像素计算出的算术均值，即
这个操作可以使用大小为mxn的一个空间滤波器来实现，滤波器的所有系数均为其值的1/mn。均值滤波平滑一幅图像中的局部变化，虽然模糊了结果，但降低了噪声。
几何均值滤波器
使用几何均值滤波器复原的一幅图像由如下表达式给出：
![\hat{f}(x,y)=[\prod_{(s,t)\in S_{xy}}g(s,t)^{}]^{\frac{1}{mn}}](http://img.e-com-net.com/image/info8/bf4fae1a195c4896b8dc92f1e1739013.gif){kind=small}
其中每个复原的像素由子图像窗口中像素的乘积的1/mn次幂给出。几何均值滤波器实现的平滑可与算术均值滤波器相比，但这种处理中丢失的图像细节更少。
谐波均值滤波器
谐波均值滤波器对于盐粒噪声效果较好，但不适用于胡椒噪声。它善于处理像高斯噪声那样的其他噪声。
逆谐波均值滤波器
其中Q称为滤波器的阶数。这种滤波器适合减少或在实际中消除椒盐噪声的影响。 当Q值为正，该滤波器消除胡椒噪声； 当Q值为负，改滤波器消除盐粒噪声。 但它不能同时消除这两种噪声。当Q=0时，逆谐波均值滤波器简化为算术均值滤波器；而当Q=-1时，则为谐波均值滤波器。
5.3.2 统计排序滤波器
统计排序滤波器是空间域滤波器，空间域滤波器的相应基于由该滤波器包围的图像区域中的像素值的顺序（排序）。排序结果决定滤波器的相应。
中值滤波器
中值滤波器使用一个像素邻域中的灰度级的中值来替代该像素的值，
中值滤波应用十分普遍，因为对于某些类型的随机噪声，它们可提供良好的去噪能力，且比相同尺寸的线性平滑滤波器引起的模糊更少。在存在单极或双极脉冲噪声的情况下，中值滤波器尤其有效。
最大值和最小值滤波器
最大值滤波器：
这种滤波器对于发现图像中的最亮点非常有用。同样，因为胡椒噪声的值非常低，作为子图像区域Sxy中这种最大值选择过程的结果，可以用这种滤波器降低它。
最小值滤波器：
这种滤波器对于发现图像中的最暗点非常有用。同样，作为最小值操作的结果，它可以降低盐粒噪声。
中点滤波器
中点滤波器简单地计算滤波器包围区域中最大值和最小值之间的中点
![\hat{f}(x,y)=\frac{1}{2}[\underset{(s,t)\in S_{xy}}{max}\left \{g(s,t) \right \}+\underset{(s,t)\in S_{xy}}{min}\left \{ g(s,t) \right \}]](http://img.e-com-net.com/image/info8/fc70beb8dca7472a9c95727d91ecd798.gif){kind=small}
这种滤波器结合了统计排序和求平均，最适用于处理随机分布的噪声，如高斯噪声或均匀噪声。
修正的阿尔法均值滤波器
式中，d的取值范围可为0到mn-1。 当d=0时，修正的阿尔法均值滤波器退化为算术均值滤波器。 如果选择d=mn-1，则修正的阿尔法均值滤波器将退化为中值滤波器。 当d取其他值时，修正的阿尔法均值滤波器在包括多种噪声的情况下很有用，如混合有高斯噪声和椒盐噪声的情况。
5.3.3 自适应滤波器
滤波器特性变化以mxn矩形窗口Sxy定义的滤波器区域内图像的统计特性为基础。
自适应局部降低噪声滤波器
随机变量最简单的统计度量是其均值和方差。作为自适应滤波器的基础，它们是合理的参数，因为它们是与图像外观紧密相关的量。均值给出了在其上计算均值的区域中的平均灰度的度量，而方差则给出了该区域的对比度的度量。
滤波器在该区域中心任意一点（x,y）上的响应基于以下四个量： （a）g(x,y)，带噪图像在点（x,y）上的值； （b）ση2，污染f(x,y)以形成g(x,y)的噪声的方差； （c）mL，Sxy中像素的局部均值； （d）σL2，Sxy中像素的局部方差。
我们希望滤波器的性能如下： 1.如果ση2为零，则滤波器应该简单地返回g(x,y)的值。这无关紧要，在零噪声情况下g(x,y)等于f(x,y)。 2.如果局部方差与ση2是高度相关的，则滤波器返回g(x,y)的一个近似值。高局部方差通常与边缘相关，并且应该保护这些边缘。 3.如果两个方差相等，我们则希望滤波器返回Sxy中像素的算数均值。这种情况发生在局部区域与整个图像有相同特性的条件下，并且就不早上将通过简单地求平均来降低。
唯一需要知道的或估计的量是全部噪声的方差
。
自适应中值滤波器
对于中值滤波器，只要脉冲噪声的空间密度不大，性能就会很好。自适应中值滤波可以处理具有更大概率的脉冲噪声，平滑非脉冲噪声时会试图保留细节，这是传统中值滤波器所做不到的。自适应中值滤波器也工作在矩形窗口区域Sxy内，但在进行滤波处理时，会根据本节列举的某些条件改变（或增大）Sxy的尺寸。滤波器的输出是单个数值，该值用于代替点(x,y)处的像素值，点(x,y)是给定时刻窗口Sxy的中心。
考虑如下符号：
- Zmin=Sxy中的最小灰度值
- Zmax=Sxy中的最大灰度值
- Zmed=Sxy中的灰度值的中值
- Zxy=坐标(x,y)处的灰度值
- Smax=Sxy允许的最大尺寸
自适应中值滤波算法以两个进程工作，分别表示为进程A和进程B
进程A：
- A1=Zmed-Zmin
- A2=Zmed-Zmax
- 如果A1>0且A2<0，则转到进程B
- 否则增大窗口尺寸
- 如果窗口尺寸≤Smax，则重复进程A
- 否则输出Zmed
进程B：
- B1=Zxy-Zmin
- B2=Zxy-Zmax
- 如果B1>0且B2<0，则输出Zxy
- 否则输出Zmed
5.4 用频率域滤波消除周期噪声
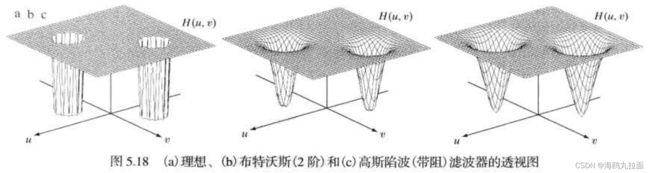
5.4.1 带阻滤波器
5.4.2 带通滤波器
带通滤波器执行与带阻滤波器相反的操作。
5.4.3 陷波滤波器
陷波滤波器阻止（或通过）事先定义的中心频率的邻域内的频率。
由于傅里叶变换的对称性，要获得有效的结果，陷波滤波器必须以关于原点对称的形式出现。这个原则的特例是，如果陷波滤波器位于原点处，在这种情况下，陷波滤波器使其本身。 可实现的陷波滤波器的对数是任意的，陷波区域的形状也可以是任意的（例如矩形）。
传递函数由下式给出：
5.4.4 最佳陷波滤波
当存在集中干扰成分时，之前的方法在滤波过程中可能会消除太多的图像信息（当图像很特别或很难获取时，很不希望出现这种现象）。 在一定意义上，最佳陷波滤波最小化了复原的估计值局部方差。
过程由两部组成：
- 第一步，提取干扰模式的主频率成分。可通过在每个尖峰处放置一个陷波带通滤波器HNP(u,v)来完成。若滤波器构建为只可通过与干扰模式相关的成分，那么干扰噪声模式的傅里叶变换由下式给出：
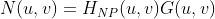G(u,v)为被污染图像的傅里叶变换。HNP(u,v)通常需要观察显示的G(u,v)的频谱交互式地创建陷波带通滤波器，来判断哪些是尖峰噪声干扰。 空间域噪声表示如下： 
- 第二步，从被污染图像中减去该模式的一个可能变权部分。因为第一步提取的知识干扰模式的主要成分（即真实干扰模式的近似值），而不是全部的噪声，故从污染图像中减去的是η(x,y)的一个加权部分，得到f(x,y)的一个估计值。
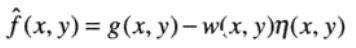
5.5 线性、位置不变的退化
假设η(x,y)=0，则g(x,y) = H[f(x,y)]。如果
则系统H是一个线性系统，其中a和b是标量，f1(x,y)和f2(x,y)是两幅输入图像。
可加性
若a=b=1，则
即，若H为线性算子，则两个输入之和的响应等于两个响应之和。
均匀性
若f2(x,y) = 0，则
表明任何与常数相乘的输入的响应，等于该输入响应乘以相同的常数。
总之，一个线性算子具有可加性和均匀性。
若一个算子满足
则满足g(x,y) = H[f(x,y)]的算子称为位置（或空间）不变系统。即，图像中任意一点处的响应只取决于该点处的输入值，而与该点的位置无关。
具有加性噪声的线性空间不变退化系统，可在空间域建模为退化（点扩散）函数与一幅图像的卷积，再加上噪声。频率域为图像与退化函数的变换的乘积，再加上噪声的变换。
用于复原处理的滤波器通常称为去卷积滤波器。
5.6 估计退化函数
在图像复原时，主要有3种用于估计退化函数的方法:（1）观察法，（2）试验法，（3）数学建模法。
5.6.1 图像观察估计
假设有一幅退化图像，而没有关于退化函数H的任何知识。基于图像被线性、位置不变的过程退化的假设，估计H的一种方法就是从图像本身来收集数据，
可基于位置不变的假设还原完整的退化函数H(u,v)。这种方法是仅在特殊环境下使用的烦琐处理。
5.6.2 试验估计
与退化图像类似的图像可以通过各种系统设置得到，直到这些图像退化到尽可能接近我们希望复原的图像。之后，使用相同的系统对一个冲激（小亮点）成像，得到退化的冲击响应。
一个冲激可由一个亮点来模拟，该点应尽可能亮，以便将噪声的影响降低到可以忽略的程度。
5.6.3 建模估计
由于退化建模能解决图像复原问题，因此多年来一直被人们使用。
大气湍流模型
k是与湍流性质有关的常数。k越大图像越模糊。
运动模糊模型
x0(t)和y0(t)分别是在x和y方向上随时间变化的运动分量。T为曝光时间，g(x,y)为模糊后的图像。
import numpy as np
import cv2
def motion_blur(image, degree=12, angle=45):
image = np.array(image)
# 这里生成任意角度的运动模糊kernel的矩阵， degree越大，模糊程度越高
M = cv2.getRotationMatrix2D((degree / 2, degree / 2), angle, 1)
motion_blur_kernel = np.diag(np.ones(degree))
motion_blur_kernel = cv2.warpAffine(motion_blur_kernel, M, (degree, degree))
motion_blur_kernel = motion_blur_kernel / degree
blurred = cv2.filter2D(image, -1, motion_blur_kernel)
# convert to uint8
cv2.normalize(blurred, blurred, 0, 255, cv2.NORM_MINMAX)
blurred = np.array(blurred, dtype=np.uint8)
return blurred
img = cv2.imread(r'G:\4.jpg')
img_ = motion_blur(img)
cv2.imshow('Source image',img)
cv2.imshow('blur image',img_)
cv2.waitKey()
处理前后对比：
5.7 逆滤波
退化函数已给出，最简单的复原方法是直接做逆滤波。这里我们用退化函数除退化图像的傅里叶变换G(u,v)来计算原始图像傅里叶变换的估计
，即
表达式告诉我们，即使知道退化函数，也不能准确地复原未退化的图像[F(u,v)的傅里叶反变换]，因为N(u,v)未知。如果退化函数是零或是非常小的值，则N(u,v)/H(u,v)很容易支配估计值。
解决退化函数为零或为非常小的值的一种方法是，限制滤波的频率，使其接近原点。因此，通过将频率限制在原点附近分析，就减少了遇到零值的概率。
5.8 最小均方误差（维纳）滤波
维纳滤波建立在图像和噪声都是随机变量的基础上，目标是找到未污染图像f的一个估计，使它们之间的均方误差最小。这种误差度量由下式给出：
假设噪声和图像不相关，其中一个或另一个有零均值，且古籍中的各灰度级是退化图像中灰度级的线性函数。基于这些条件，误差函数的最小值在频率域中由如下表达式给出：
式中各项意义如下：
- H(u,v)=退化函数
- H*(u,v)=H(u,v)的复共轭
- |H(u,v)|²=H*(u,v)H(u,v)
- Sη(u,v)=|N(u,v)|²=噪声的功率谱
- Sf(u,v)=|F(u,v)|²=未退化图像的功率谱
许多有用的度量是以噪声和未退化图像的功率谱为基础的，其中最重要的一种是信噪比，它在频率域中用下式来近似：
该比值给出了携带信息的信号功率（即原始的或退化的原图像）水平与噪声功率水平的度量。
当处理白噪声时，谱|N(u,v)|²是一个常数。然而，未退化图像的功率谱很少是已知的。当这些量未知或不能估计时，经常使用的一种方法下面的表达式：
式中K是一个加到|H(u,v)|²的所有项上的特定常数。
5.9 约束最小二乘方滤波
其中γ是一个参数，可以对γ进行交互式的调整，也可以对其进行迭代计算。P(u,y)是矩阵p(x,y) = [0, -1, 0; -1, 4,-1; 0, -1, 0]的傅里叶变换。该算法相比于维纳滤波，对其应用的每幅图像都能产生最优的结果。
5.10 几何均值滤波
对维纳滤波器稍加推广就是所谓的几何均值滤波器形式：
其中α和β是正的实常数。
以下给出算术均值滤波、几何均值滤波器、谐波滤波器处理代码及结果、
import numpy as np
import cv2
# 算术均值滤波器：
def a_mean(img, kernel_size):
G_mean_img = np.zeros(img.shape)
# print(G_mean_img[0][0])
# print(img)
k = int((kernel_size - 1) / 2)
# print(k)
for i in range(img.shape[0]):
for j in range(img.shape[1]):
if i < k or i > (img.shape[0] - k - 1) or j < k or j > (img.shape[1] - k - 1):
G_mean_img[i][j] = img[i][j]
else:
for n in range(kernel_size):
for m in range(kernel_size):
G_mean_img[i][j] += np.float(1 / (kernel_size * kernel_size) * img[i - k + n][j - k + m])
# G_mean_img[i][j]=1/9*(img[i-1][j-1]+img[i-1][j]+img[i-1][j+1]+img[i][j-1]+img[i][j]+img[i][j+1]+img[i+1][j-1]+img[i+1][j]+img[i+1][j+1])
G_mean_img = np.uint8(G_mean_img)
return G_mean_img
# 几何均值滤波器：
def G_mean(img, kernel_size):
G_mean_img = np.ones(img.shape)
# print(G_mean_img[0][0])
# print(img)
k = int((kernel_size - 1) / 2)
# print(k)
for i in range(img.shape[0]):
for j in range(img.shape[1]):
if i < k or i > (img.shape[0] - k - 1) or j < k or j > (img.shape[1] - k - 1):
G_mean_img[i][j] = img[i][j]
else:
for n in range(kernel_size):
for m in range(kernel_size):
G_mean_img[i][j] *= np.float(img[i - k + n][j - k + m])
G_mean_img[i][j] = pow(G_mean_img[i][j], 1 / (kernel_size * kernel_size))
# G_mean_img[i][j]=1/9*(img[i-1][j-1]+img[i-1][j]+img[i-1][j+1]+img[i][j-1]+img[i][j]+img[i][j+1]+img[i+1][j-1]+img[i+1][j]+img[i+1][j+1])
G_mean_img = np.uint8(G_mean_img)
return G_mean_img
# 谐波均值滤波器：
def H_mean(img, kernel_size):
G_mean_img = np.zeros(img.shape)
# print(G_mean_img[0][0])
# print(img)
k = int((kernel_size - 1) / 2)
# print(k)
for i in range(img.shape[0]):
for j in range(img.shape[1]):
if i < k or i > (img.shape[0] - k - 1) or j < k or j > (img.shape[1] - k - 1):
G_mean_img[i][j] = img[i][j]
else:
for n in range(kernel_size):
for m in range(kernel_size):
if img[i - k + n][j - k + m] == 0:
G_mean_img[i][j] = 0
break
else:
G_mean_img[i][j] += 1 / np.float(img[i - k + n][j - k + m])
else:
continue
break
if G_mean_img[i][j] != 0:
G_mean_img[i][j] = (kernel_size * kernel_size) / G_mean_img[i][j]
# G_mean_img[i][j]=1/9*(img[i-1][j-1]+img[i-1][j]+img[i-1][j+1]+img[i][j-1]+img[i][j]+img[i][j+1]+img[i+1][j-1]+img[i+1][j]+img[i+1][j+1])
G_mean_img = np.uint8(G_mean_img)
return G_mean_img
# 逆谐波均值滤波器：
def HT_mean(img, kernel_size, Q):
G_mean_img = np.zeros(img.shape)
# print(G_mean_img[0][0])
# print(img)
k = int((kernel_size - 1) / 2)
# print(k)
for i in range(img.shape[0]):
for j in range(img.shape[1]):
if i < k or i > (img.shape[0] - k - 1) or j < k or j > (img.shape[1] - k - 1):
G_mean_img[i][j] = img[i][j]
else:
result_top = 0
result_down = 0
for n in range(kernel_size):
for m in range(kernel_size):
if Q > 0:
result_top += pow(np.float(img[i - k + n][j - k + m]), Q + 1)
result_down += pow(np.float(img[i - k + n][j - k + m]), Q)
else:
if img[i - k + n][j - k + m] == 0:
G_mean_img[i][j] = 0
break
else:
result_top += pow(np.float(img[i - k + n][j - k + m]), Q + 1)
result_down += pow(np.float(img[i - k + n][j - k + m]), Q)
else:
continue
break
else:
if result_down != 0:
G_mean_img[i][j] = result_top / result_down
# G_mean_img[i][j]=1/9*(img[i-1][j-1]+img[i-1][j]+img[i-1][j+1]+img[i][j-1]+img[i][j]+img[i][j+1]+img[i+1][j-1]+img[i+1][j]+img[i+1][j+1])
G_mean_img = np.uint8(G_mean_img)
return G_mean_img
if __name__ == "__main__":
img = cv2.imread('G:\\5.JPG', 0)
G_mean_img_3 = HT_mean(img, kernel_size=3, Q=-1.5)
G_mean_img_5 = HT_mean(img, kernel_size=5, Q=-1.5)
G_mean_img_9 = HT_mean(img, kernel_size=9, Q=-1.5)
print(G_mean_img_3.max())
cv2.imshow("show1", img)
cv2.imshow("show2_3", G_mean_img_3)
cv2.imshow("show3_5", G_mean_img_5)
cv2.imshow("show3_9", G_mean_img_9)
cv2.waitKey(0)
print("test_end")
按顺序分别为原图、算术均值图、几何均值图、谐波均值图