从零点五开始的深度学习笔记——VAE(Variational AutoEncoder) (三)VAE的简单实现
VAE的简单实现
- 学习笔记链接
- 1. 预备知识
-
- 1.1 关于采样
-
- 1.1.1 蒙特卡罗模拟
- 1.1.2 重要性采样
- 1.2 VAE模型的假设
-
- 1.2.1 关于采样
- 1.2.2 编码器 p ( z ∣ x ) p(z|x) p(z∣x)部分
- 1.2.3 隐变量 q ( z ) q(z) q(z)部分
- 1.2.4 解码器 q ( x ∣ z ) q(x|z) q(x∣z)部分
- 1.2.5 小结
- 2. VAE的实现
-
- 2.1 重参数化
- 2.2 以MNIST手写数字图片为例
-
- 2.2.1 MNIST数据下载
- 2.2.2 传统的的自编码器
- 2.2.4 训练结果
- 2.3 VAE
-
- 2.3.1 模型
- 2.3.2 训练
- 2.3.3 训练结果
学习笔记链接
从零点五开始的深度学习笔记——VAE(Variational AutoEncoder) (一) 预备知识
从零点五开始的深度学习笔记——VAE(Variational AutoEncoder) (二)概率角度理解VAE结构
1. 预备知识
1.1 关于采样
1.1.1 蒙特卡罗模拟
蒙特卡罗,蒙特卡洛,Monte Carlo是一个赌场的名字,这名字起得就很有概率统计学的意思。部分参考苏剑林. (Mar. 28, 2018). 《变分自编码器(二):从贝叶斯观点出发 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/5343 教程。下面我们将介绍如何求一个满足 p ( x ) p(x) p(x)概率分布的随机变量 x x x的期望的过程,首先在连续空间中分析, E x ∼ p ( x ) [ x ] = ∫ x p ( x ) d x \mathbb{E}_{x\sim p(x)}\left[x\right]=\int xp(x)dx Ex∼p(x)[x]=∫xp(x)dx, 如果使用计算机来硬算的话,一个简单的方式是将他离散化再累加起来:
E x ∼ p ( x ) [ x ] ≈ ∑ i x i p ( x i ) ( x i − x i − 1 ) \begin{equation} \mathbb{E}_{x\sim p(x)}\bigg[x\bigg] \approx \sum_i x_ip(x_i)(x_i-x_{i-1}) \end{equation} Ex∼p(x)[x]≈i∑xip(xi)(xi−xi−1)
根据统计学中的大数定理,一个随机变量的期望等于这个随机变量在 n → ∞ n\rightarrow\infty n→∞次试验后,所有取值的平均值。所以计算机可以对采样进行模拟,然后将所有取值求平均,从而得到该变量的期望:
E x ∼ p ( x ) [ x ] ≈ 1 n ∑ i = 1 n x i , x i ∼ p ( x ) \begin{equation} \mathbb{E}_{x\sim p(x)}\bigg[x\bigg] \approx \frac{1}{n} \sum_{i=1}^n x_i, ~~~~~x_i\sim p(x) \end{equation} Ex∼p(x)[x]≈n1i=1∑nxi, xi∼p(x)
更一般的,
E x ∼ p ( x ) [ f ( x ) ] ≈ 1 n ∑ i = 1 n f ( x i ) , x i ∼ p ( x ) \begin{equation} \mathbb{E}_{x\sim p(x)}\bigg[f(x)\bigg] \approx \frac{1}{n} \sum_{i=1}^n f(x_i), ~~~~~x_i\sim p(x) \end{equation} Ex∼p(x)[f(x)]≈n1i=1∑nf(xi), xi∼p(x)
1.1.2 重要性采样
上面解决了期望计算的问题,但还需要对 x x x根据概率分布 p ( x ) p(x) p(x)进行采样,这就不得不提重要性采样, MCMC采样等从一个已知分布中对随机变量进行采样的采样方法了。后续涉及到再补充。
1.2 VAE模型的假设
实际上上一篇博文从零点五开始的深度学习笔记——VAE(Variational AutoEncoder) (二)概率角度理解VAE结构的目标函数是一般化的,并非VAE特有,根据理论公式的指导,VAE对网络的具体构造和实现进行了一定的假设,使之实现网络生成的功能。回顾一下这条理想状态下的VAE的损失函数:
D K L ( p ( x , z ) ∣ ∣ q ( x , z ) ) = E x ∼ p ( x ) [ E z ∼ p ( z ∣ x ) [ − l o g ( q ( x ∣ z ) ) ] + D K L ( p ( z ∣ x ) ∣ ∣ q ( z ) ) ] + c o n s t \begin{equation} \mathbb{D}_{KL}\left(p(x, z)\bigg|\bigg|q(x, z)\right) = \mathbb{E}_{x\sim p(x)}\bigg[\mathbb{E}_{z\sim p(z|x)} \bigg[-log(q(x|z))\bigg] + \mathbb{D}_{KL}\left(p(z|x)\bigg|\bigg|q(z)\right)\bigg] + const \end{equation} DKL(p(x,z)∣ ∣∣ ∣q(x,z))=Ex∼p(x)[Ez∼p(z∣x)[−log(q(x∣z))]+DKL(p(z∣x)∣ ∣∣ ∣q(z))]+const
为什么说这条公式具有指导意义?因为他告诉了我们所有相关的随机变量是在什么概率分布下采样出来的(虽然采样的概率分布可能是未知的),且如果设计了一个网络,这个网络应该需要逼近哪些项,如果模型极限效果提不上去,是由于我们做了什么理想的假设使得模型于这纷繁复杂的世界之间存在reality gap。当然,这些假设的存在往往是为了简化问题的解决难度,如下文所示:
1.2.1 关于采样
上面我们简单提到了蒙特卡洛采样的思想。如果我们数据足够庞大的话,上面的损失函数可以简写为:
D K L ( p ( x , z ) ∣ ∣ q ( x , z ) ) = E z ∼ p ( z ∣ x ) [ − l o g ( q ( x ∣ z ) ) ] + D K L ( p ( z ∣ x ) ∣ ∣ q ( z ) ) \begin{equation} \mathbb{D}_{KL}\left(p(x, z)\bigg|\bigg|q(x, z)\right) = \mathbb{E}_{z\sim p(z|x)} \bigg[-log(q(x|z))\bigg] + \mathbb{D}_{KL}\left(p(z|x)\bigg|\bigg|q(z)\right) \end{equation} DKL(p(x,z)∣ ∣∣ ∣q(x,z))=Ez∼p(z∣x)[−log(q(x∣z))]+DKL(p(z∣x)∣ ∣∣ ∣q(z))
为什么?因为我们的训练输入数据就是已经遵循了某个未知的规律采回来的,狗有狗的样子,采样回来不会变成猫的样子。只要不是人工合成的数据,我们所获得的训练集在冥冥之中已经遵循了某种规律。也因此,我们可以把这个理想的损失函数最外层的剥离。这一步假设成立的前提是训练集足够庞大,能够比较好地体现采样分布。
继续观察这个函数,涉及到了几个部分,理想模型中的 p ( z ∣ x ) p(z|x) p(z∣x), 待估计网络的 q ( z ) q(z) q(z)和 q ( x ∣ z ) q(x|z) q(x∣z)。不难理解,这三项正好对应了,编码器,隐空间(latent space, latent vector, bottle neck,都是它),以及解码器。
1.2.2 编码器 p ( z ∣ x ) p(z|x) p(z∣x)部分
简化后的损失函数还是具有一定的缺陷,涉及到蛋鸡问题。为了拟合这个未知模型需要已知理想的 p ( z ∣ x ) p(z|x) p(z∣x)。我猜研究人员把公式推到这里后,实在是不能忍,想要窥探VAE的真容却在此刻吃了只苍蝇。所以只能硬着头皮把这一项用万物皆可神经网络拟合来继续向前探索了。
p ( z ∣ x ) p(z|x) p(z∣x)编码器也使用神经网络拟合。由于最终需要拟合的是一个概率分布用于后续的采样,从而得到隐变量 z z z,所以继续引入了假设,假设这个概率分布是一个多变量高斯函数,即多变量正态分布函数。则,神经网络的输出为隐变量 z z z各个维度的均值和方差。总而言之,就是每一个维度的 z z z都是一个高斯函数, 即 z i ∼ N ( μ i ( x ) , σ i 2 ( x ) ) z_i \sim \mathcal{N}(\mu_i(x), \sigma_i^2(x)) zi∼N(μi(x),σi2(x))
p ( z ∣ x ) = N ( μ ( x ) , d i a g ( σ i 2 ( x ) ) ) , i = 1 , 2 , . . . , k , z ∈ R k = 1 ∏ i = 1 k 2 π σ i 2 ( x ) e x p ( − 1 2 ∑ i = 1 k ( z i − μ i ( x ) ) 2 σ i 2 ( x ) ) \begin{equation} \begin{aligned} p(z|x) =& \mathcal{N}\bigg(\mu(x), diag\big(\sigma_i^2(x)\big) \bigg), ~~i=1,2, ..., k,~~z\in\mathbb{R}^k \\ =& \frac{1}{\prod_{i=1}^k \sqrt{2\pi\sigma_i^2(x)}} exp\left(-\frac{1}{2} \sum_{i=1}^k \frac{(z_i-\mu_i(x))^2}{\sigma_i^2(x)}\right) \\ \end{aligned} \end{equation} p(z∣x)==N(μ(x),diag(σi2(x))), i=1,2,...,k, z∈Rk∏i=1k2πσi2(x)1exp(−21i=1∑kσi2(x)(zi−μi(x))2)
1.2.3 隐变量 q ( z ) q(z) q(z)部分
q ( z ) q(z) q(z)这一部分就是完全可控的了,可以由我们自己设计。那当然是一切从简,所以,直接假定这个分布是标准正态分布,可以让整个世界都变得很美好。
p ( z ) = N ( 0 , I ) p(z) = \mathcal{N}\left(\mathbf{0}, I\right) p(z)=N(0,I)
回顾从零点五开始的深度学习笔记——VAE(Variational AutoEncoder) (一) 预备知识 中我们推导得到的公式:
D K L ( P ∣ ∣ Q ) = 1 2 [ l o g ∣ Σ 2 ∣ ∣ Σ 1 ∣ − k + t r ( Σ 2 − 1 Σ 1 ) + ( μ 2 − μ 1 ) T Σ 2 − 1 ( μ 2 − μ 1 ) ] \begin{equation} \mathbb{D}_{KL}(P||Q) = \frac{1}{2} \left[ log\frac{|\Sigma_2|}{|\Sigma_1|} - k + tr(\Sigma_2^{-1}\Sigma_1) + (\mu_2-\mu_1)^T\Sigma_2^{-1}(\mu_2-\mu_1)\right] \end{equation} DKL(P∣∣Q)=21[log∣Σ1∣∣Σ2∣−k+tr(Σ2−1Σ1)+(μ2−μ1)TΣ2−1(μ2−μ1)]
将 q ( z ) q(z) q(z)和 p ( z ∣ x ) p(z|x) p(z∣x)代入到上式中,可得:
D K L ( p ( z ∣ x ) ∣ ∣ q ( z ) ) = 1 2 ∑ i = 1 k ( σ i 2 ( x ) + μ i 2 ( x ) − l o g ( σ i 2 ( x ) ) − 1 ) \mathbb{D}_{KL}\bigg(p(z|x)\bigg|\bigg|q(z)\bigg) = \frac{1}{2} \sum_{i=1}^k\bigg(\sigma_i^2(x)+\mu_i^2(x)-log(\sigma_i^2(x))-1\bigg) DKL(p(z∣x)∣ ∣∣ ∣q(z))=21i=1∑k(σi2(x)+μi2(x)−log(σi2(x))−1)
1.2.4 解码器 q ( x ∣ z ) q(x|z) q(x∣z)部分
这部分的理解参考了苏剑林. (Mar. 28, 2018). 《变分自编码器(二):从贝叶斯观点出发 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/5343的分析。解码器的模型候选方案需要输出的是一个容易计算,且满足概率分布函数积分为1的归一化约束。因此,可选择的方案不多。有伯努利分布和正态分布模型。
- 正态分布模型
和 p ( z ∣ x ) p(z|x) p(z∣x)相同,
q ( x ∣ z ) = N ( μ ˉ ( z ) , d i a g ( σ ˉ i 2 ( z ) ) ) , i = 1 , 2 , . . . , n , x ∈ R n q(x|z) = \mathcal{N}\bigg(\bar\mu(z), diag\big(\bar\sigma_i^2(z)\big) \bigg), ~~i=1,2, ..., n,~~x\in\mathbb{R}^n q(x∣z)=N(μˉ(z),diag(σˉi2(z))), i=1,2,...,n, x∈Rn
则,损失函数的第一项可展开为:
− l o g ( q ( x ∣ z ) ) = 1 2 ∑ i = 1 n ( z i − μ ˉ i ( z ) ) 2 σ ˉ i 2 ( z ) + 1 2 ∑ i = 1 n l o g ( σ ˉ i 2 ( z ) ) + n 2 l o g ( 2 π ) -log\bigg(q(x|z)\bigg) = \frac{1}{2} \sum_{i=1}^n \frac{(z_i-\bar\mu_i(z))^2}{\bar\sigma_i^2(z)} + \frac{1}{2}\sum_{i=1}^n log(\bar\sigma_i^2(z)) + \frac{n}{2}log(2\pi) −log(q(x∣z))=21i=1∑nσˉi2(z)(zi−μˉi(z))2+21i=1∑nlog(σˉi2(z))+2nlog(2π)
1.2.5 小结
因此,按照这何种结构选择,最终的损失函数的计算可简化为:
D K L ( p ( x , z ) ∣ ∣ q ( x , z ) ) = E z ∼ p ( z ∣ x ) [ 1 2 ∑ i = 1 n ( z i − μ ˉ i ( z ) ) 2 σ ˉ i 2 ( z ) + 1 2 ∑ i = 1 n l o g ( σ ˉ i 2 ( z ) ) + n 2 l o g ( 2 π ) ] + 1 2 ∑ i = 1 k ( σ i 2 ( x ) + μ i 2 ( x ) − l o g ( σ i 2 ( x ) ) − 1 ) \begin{equation} \begin{aligned} &\mathbb{D}_{KL}\bigg(p(x, z)\bigg|\bigg|q(x, z)\bigg) \\ =& \mathbb{E}_{z\sim p(z|x)}\Bigg[ \frac{1}{2} \sum_{i=1}^n \frac{(z_i-\bar\mu_i(z))^2}{\bar\sigma_i^2(z)} + \frac{1}{2}\sum_{i=1}^n log(\bar\sigma_i^2(z)) + \frac{n}{2}log(2\pi)\Bigg]\\ &+ \frac{1}{2} \sum_{i=1}^k\bigg(\sigma_i^2(x)+\mu_i^2(x)-log(\sigma_i^2(x))-1\bigg) \\ \end{aligned} \end{equation} =DKL(p(x,z)∣ ∣∣ ∣q(x,z))Ez∼p(z∣x)[21i=1∑nσˉi2(z)(zi−μˉi(z))2+21i=1∑nlog(σˉi2(z))+2nlog(2π)]+21i=1∑k(σi2(x)+μi2(x)−log(σi2(x))−1)
注意,这里的算是函数跟一般的损失函数不太一样,有个期望在这里,在训练模型的时候,需要对这一项进行采样,从实践结果来看,可以用采样一次的结果来表示期望的值。因此, 参考苏剑林. (Mar. 28, 2018). 《变分自编码器(二):从贝叶斯观点出发 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/5343,整个VAE的损失函数的一般性写法是:
L = D K L ( p ( x , z ) ∣ ∣ q ( x , z ) ) = E z ∼ p ( z ∣ x ) [ − l o g ( q ( x ∣ z ) ) + D K L ( p ( z ∣ x ) ∣ ∣ q ( z ) ) ] , z ∼ p ( z ∣ x ) \begin{equation} \begin{aligned} \mathcal{L}=&\mathbb{D}_{KL}\bigg(p(x, z)\bigg|\bigg|q(x, z)\bigg) \\ =& \mathbb{E}_{z\sim p(z|x)}\bigg[ -log(q(x|z)) + \mathbb{D}_{KL}\bigg(p(z|x)\bigg|\bigg|q(z)\bigg) \bigg], ~~ z\sim p(z|x) \end{aligned} \end{equation} L==DKL(p(x,z)∣ ∣∣ ∣q(x,z))Ez∼p(z∣x)[−log(q(x∣z))+DKL(p(z∣x)∣ ∣∣ ∣q(z))], z∼p(z∣x)
2. VAE的实现
2.1 重参数化
重参数化 (reparameterizatin) 是VAE编程实现很重要的小技巧,有了它才能够让网络反向传播,计算梯度,更新网络权值。它使用到了正态分布采样的一个等价的方法:在标准正态分布 N ( 0 , I ) \mathcal{N}\big(\mathbf{0}, \mathbf{I}\big) N(0,I)中采样得到 ϵ \epsilon ϵ后,对采样结果进行放缩 σ \mathbf{\sigma} σ和位移 μ \mathbf{\mu} μ可以使得到的采样结果( μ + σ ϵ \mu + \sigma\epsilon μ+σϵ)与另一个相关的正态分布 N ( μ , σ 2 ) \mathcal{N}\big(\mu, \sigma^2\big) N(μ,σ2)采样结果一致。这种采样方式之所以称为小技巧是因为这种操作是为了适配当前编程软件自动梯度求解功能所做的操作。
2.2 以MNIST手写数字图片为例
2.2.1 MNIST数据下载
'''
Author : Dianye Huang
Date : 2022-08-23 10:04:45
LastEditTime: 2022-08-26 22:02:34
Description :
'''
from torch.utils.data import DataLoader
import torchvision
from torchvision.datasets import mnist
import torchvision.transforms as transforms
class ExpDataLoader(object):
def __init__(self) -> None:
self.to_pil_image = transforms.ToPILImage()
def vis_img(self, img):
vis = self.to_pil_image(img)
vis.show()
def vis_grid_imgs(self, imgs, nrow=8):
grid = torchvision.utils.make_grid(imgs, nrow=nrow)
self.vis_img(grid)
def get_mnist_dataset(self, dir='./data', ):
train_set=mnist.MNIST(dir, train=True,
transform=torchvision.transforms.ToTensor(),
download=True)
test_set=mnist.MNIST(dir, train=False,
transform=torchvision.transforms.ToTensor(),
download=True)
return train_set, test_set
def get_mnist_dataloader(self, dir='./data', batch_size = 16):
mnist_train_ds, mnist_test_ds = self.get_mnist_dataset(dir=dir)
train_loader = DataLoader(dataset=mnist_train_ds,
batch_size=batch_size,
shuffle=True)
test_loader = DataLoader(dataset=mnist_test_ds,
batch_size=batch_size,
shuffle=False)
return train_loader, test_loader
下载数据生成dataloader
if __name__ == '__main__':
# load data
exp_dataloader = ExpDataLoader()
data_dir = '/home/dianye/DNN_ws/CSDN_tutorials/VAEs'
train_loader, test_loader = exp_dataloader.get_mnist_dataloader(dir=data_dir, batch_size=128)
2.2.2 传统的的自编码器
从 https://avandekleut.github.io/vae/ 中复制过来的一段最最原始的自编码器代码,简单粗暴地拟合输入输出。
import torch
from torch import nn
import torch.nn.functional as F
'''
Typical Auto Encoder:
https://avandekleut.github.io/vae/
'''
class Encoder(nn.Module):
def __init__(self, latent_dims):
super(Encoder, self).__init__()
self.linear1 = nn.Linear(784, 512)
self.linear2 = nn.Linear(512, latent_dims)
def forward(self, x):
x = torch.flatten(x, start_dim=1)
x = F.relu(self.linear1(x))
return self.linear2(x)
class Decoder(nn.Module):
def __init__(self, latent_dims):
super(Decoder, self).__init__()
self.linear1 = nn.Linear(latent_dims, 512)
self.linear2 = nn.Linear(512, 784)
def forward(self, z):
z = F.relu(self.linear1(z))
z = torch.sigmoid(self.linear2(z))
return z.reshape((-1, 1, 28, 28))
class Autoencoder(nn.Module):
def __init__(self, latent_dims):
super(Autoencoder, self).__init__()
self.encoder = Encoder(latent_dims)
self.decoder = Decoder(latent_dims)
def forward(self, x):
z = self.encoder(x)
return self.decoder(z)
开始训练,下面的代码主要参考了https://avandekleut.github.io/vae/,加了点小修改。
'''
Author : Dianye Huang
Date : 2022-08-23 10:04:45
LastEditTime: 2022-08-26 22:08:16
Description :
'''
import torch
import torchvision
from vae_utils import ExpDataLoader
from vae_zoo import Autoencoder
import matplotlib.pyplot as plt
import numpy as np
# device = 'cuda' if torch.cuda.is_available() else 'cpu'
from tqdm import tqdm
device = 'cpu'
def train_ae(autoencoder, data, epochs=20):
opt = torch.optim.Adam(autoencoder.parameters())
for epoch in range(epochs):
print('Epoch:', epoch)
for x, y in tqdm(data):
x = x.to(device) # GPU
opt.zero_grad()
x_hat = autoencoder(x)
loss = ((x - x_hat)**2).sum()
loss.backward()
opt.step()
return autoencoder
def plot_latent(autoencoder, data, num_batches=100):
for i, (x, y) in enumerate(data):
z = autoencoder.encoder(x.to(device))
z = z.to('cpu').detach().numpy()
plt.scatter(z[:, 0], z[:, 1], c=y, cmap='tab10')
if i > num_batches:
plt.colorbar()
break
def plot_reconstructed(autoencoder, r0=(-5, 10), r1=(-10, 5), n=12):
w = 28
img = np.zeros((n*w, n*w))
for i, y in enumerate(np.linspace(*r1, n)):
for j, x in enumerate(np.linspace(*r0, n)):
z = torch.Tensor([[x, y]]).to(device)
x_hat = autoencoder.decoder(z)
x_hat = x_hat.reshape(28, 28).to('cpu').detach().numpy()
img[(n-1-i)*w:(n-1-i+1)*w, j*w:(j+1)*w] = x_hat
plt.imshow(img, extent=[*r0, *r1])
if __name__ == '__main__':
# load data
exp_dataloader = ExpDataLoader()
data_dir = '/home/dianye/DNN_ws/CSDN_tutorials/VAEs'
train_loader, test_loader = exp_dataloader.get_mnist_dataloader(dir=data_dir, batch_size=128)
# start training
device = 'cpu'
latent_dims = 2
autoencoder = Autoencoder(latent_dims).to(device) # GPU
autoencoder = train_ae(autoencoder, train_loader, epochs=20)
# visualize result
plt.figure(1)
plot_latent(autoencoder, train_loader)
plt.figure(2)
plot_reconstructed(autoencoder)
plt.pause(0)
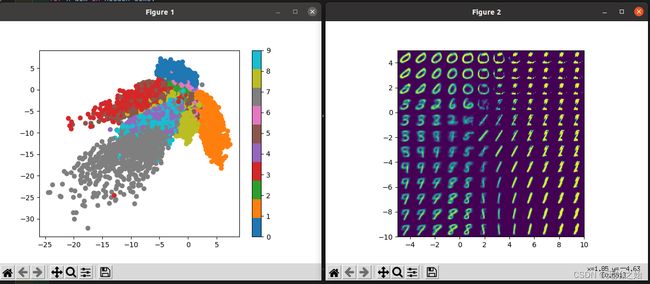
2.2.4 训练结果
2.3 VAE
2.3.1 模型
VAE编程的时候,需要损失函数的写法。第一点是,bottleneck部分,两个全连接层输出的分别是均值 μ \mu μ和方差 log ( σ 2 ) \log(\sigma^2) log(σ2)。因此在计算KL散度的时候会有exp的运算。对于模型拟合误差项为什么是一个输入输出的平方差之和,可以观察我们损失函数的第一项:
D K L ( p ( x , z ) ∣ ∣ q ( x , z ) ) = E z ∼ p ( z ∣ x ) [ 1 2 ∑ i = 1 n ( z i − μ ˉ i ( z ) ) 2 σ ˉ i 2 ( z ) + 1 2 ∑ i = 1 n l o g ( σ ˉ i 2 ( z ) ) + n 2 l o g ( 2 π ) ] + 1 2 ∑ i = 1 k ( σ i 2 ( x ) + μ i 2 ( x ) − l o g ( σ i 2 ( x ) ) − 1 ) \begin{equation} \begin{aligned} &\mathbb{D}_{KL}\bigg(p(x, z)\bigg|\bigg|q(x, z)\bigg) \\ =& \mathbb{E}_{z\sim p(z|x)}\Bigg[ \frac{1}{2} \sum_{i=1}^n \frac{(z_i-\bar\mu_i(z))^2}{\bar\sigma_i^2(z)} + \frac{1}{2}\sum_{i=1}^n log(\bar\sigma_i^2(z)) + \frac{n}{2}log(2\pi)\Bigg]\\ &+ \frac{1}{2} \sum_{i=1}^k\bigg(\sigma_i^2(x)+\mu_i^2(x)-log(\sigma_i^2(x))-1\bigg) \\ \end{aligned} \end{equation} =DKL(p(x,z)∣ ∣∣ ∣q(x,z))Ez∼p(z∣x)[21i=1∑nσˉi2(z)(zi−μˉi(z))2+21i=1∑nlog(σˉi2(z))+2nlog(2π)]+21i=1∑k(σi2(x)+μi2(x)−log(σi2(x))−1)
p ( z ∣ x ) p(z|x) p(z∣x)是解码器,采样服从的分布,而我们实际计算前向传播的时候,并没有用到方差,而是认为方差是个常数,直接以概率1将 z z z不做任何处理直接扔到解码器里。这样,优化损失函数的第一项,就相当于优化 1 2 ∑ i = 1 n ( z i − μ ˉ i ( z ) ) 2 σ ˉ i 2 ( z ) \frac{1}{2} \sum_{i=1}^n \frac{(z_i-\bar\mu_i(z))^2}{\bar\sigma_i^2(z)} 21∑i=1nσˉi2(z)(zi−μˉi(z))2中的平方xiang,即 1 2 σ ˉ i 2 ( z ) ∑ i = 1 n ( z i − μ ˉ i ( z ) ) 2 = c o n s t × ∥ z − d e c o d e r ( z ) ∥ 2 \frac{1}{2\bar\sigma_i^2(z)} \sum_{i=1}^n (z_i-\bar\mu_i(z))^2=const\times\|z - decoder(z)\|^2 2σˉi2(z)1∑i=1n(zi−μˉi(z))2=const×∥z−decoder(z)∥2。
'''
Author : Dianye Huang
Date : 2022-08-23 10:04:45
LastEditTime : 2022-08-27 01:34:39
Description :
'''
import torch
from torch import nn
import torch.nn.functional as F
'''
Typical Variational Auto Encoder
'''
class VanillaVAE(nn.Module):
def __init__(self,
in_channels:int = 784, # 28*28
latent_dim: int = 2,
hidden_dims: list = [512]
) -> None:
super(VanillaVAE, self).__init__()
self.in_channels = in_channels
# Build Encoder
modules = []
for h_dim in hidden_dims:
modules.append(
nn.Sequential(
nn.Linear(in_channels, h_dim),
nn.ReLU()
)
)
in_channels = h_dim
self.encoder = nn.Sequential(*modules)
# Bottle Neck
self.latent_dim = latent_dim
self.fc_mu = nn.Linear(hidden_dims[-1], latent_dim)
self.fc_var = nn.Linear(hidden_dims[-1], latent_dim)
# Build Decoder
modules = []
in_ch = latent_dim
hidden_dims.reverse()
for h_dim in hidden_dims:
modules.append(
nn.Sequential(
nn.Linear(in_ch, h_dim),
nn.ReLU()
)
)
in_ch = h_dim
self.decoder = nn.Sequential(*modules)
# Output Layer
self.output_layer = nn.Sequential(
nn.Linear(hidden_dims[-1], self.in_channels),
nn.Sigmoid())
def encode(self, input:torch.tensor):
return self.encoder(input)
def bottleneck(self, input:torch.tensor):
mu = self.fc_mu(input)
log_var = self.fc_var(input)
return self.reparameterize(mu, log_var)
def decode(self, z: torch.tensor):
return self.decoder(z)
def reparameterize(self, mu, logvar):
std = torch.exp(0.5 * logvar)
eps = torch.randn_like(std) # 返回一个和输入大小相同的张量,其由均值为0、方差为1的标准正态分布填充
return eps*std + mu
def forward(self, input: torch.tensor):
x = torch.flatten(input, start_dim=1)
out = self.encoder(x)
mu = self.fc_mu(out)
logvar = self.fc_var(out)
z = self.reparameterize(mu, logvar)
out = self.decoder(z)
out = self.output_layer(out)
return out, x, mu, logvar
def loss_function(self, x_hat, x, mu, logvar):
D_KL = 0.5*(torch.exp(logvar) + mu**2 - logvar - 1).sum()
recon_loss = 10*((x_hat - x)**2).sum()
return recon_loss + D_KL
2.3.2 训练
'''
Author : Dianye Huang
Date : 2022-08-23 10:04:45
LastEditTime: 2022-08-27 00:43:14
Description :
'''
import torch
from vae_utils import ExpDataLoader
from vae_zoo import Autoencoder, VanillaVAE
import matplotlib.pyplot as plt
import numpy as np
from tqdm import tqdm
device = 'cpu'
if __name__ == '__main__':
# load data
exp_dataloader = ExpDataLoader()
data_dir = '/home/dianye/DNN_ws/CSDN_tutorials/VAEs'
train_loader, test_loader = exp_dataloader.get_mnist_dataloader(dir=data_dir, batch_size=128)
# start training variational auto encoder
vae = VanillaVAE(latent_dim=2).to(device)
opt = torch.optim.Adam(vae.parameters())
for epoch in range(20):
pbar = tqdm(train_loader, desc='description')
for x, y in pbar:
x = x.to(device)
opt.zero_grad()
x_hat, x, mu, logvar = vae(x)
loss = vae.loss_function(x_hat, x, mu, logvar)
loss.backward()
opt.step()
pbar.set_description(f"Epoch: {epoch+1}, loss: {round(float(loss.to('cpu').detach().numpy()),3)}")
plt.figure(1)
with torch.no_grad():
for i, (x, y) in enumerate(train_loader):
z_tmp = vae.encoder(torch.flatten(x.to(device), start_dim=1))
z = vae.bottleneck(z_tmp)
z = z.to('cpu').detach().numpy()
plt.scatter(z[:, 0], z[:, 1], c=y, cmap='tab10')
if i > 100:
plt.colorbar()
break
plt.figure(2)
with torch.no_grad():
r0=(-5, 10)
r1=(-10, 5)
n=12
w = 28
img = np.zeros((n*w, n*w))
for i, y in enumerate(np.linspace(*r1, n)):
for j, x in enumerate(np.linspace(*r0, n)):
z = torch.Tensor([[x, y]]).to(device)
x_tmp = vae.decoder(z)
x_hat = vae.output_layer(x_tmp)
x_hat = x_hat.reshape(28, 28).to('cpu').detach().numpy()
img[(n-1-i)*w:(n-1-i+1)*w, j*w:(j+1)*w] = x_hat
plt.imshow(img, extent=[*r0, *r1])
plt.show()
2.3.3 训练结果
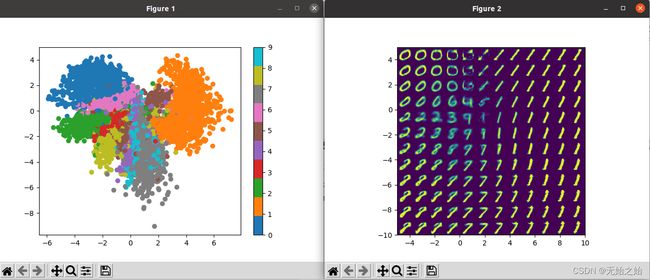
以上。VAE部分理解得差不多就行了,后续的博客将会介绍conditional VAE。
祝周末愉快!
2022年8月27日
Dianye Huang