万字总结MATLAB中的图形绘制

目录

二维曲线

1. plot函数

 2.fplot函数

3.fimplicit函数

 4.polarplot函数

 5.contour函数和contourf函数

6.semilogx函数、semilogy函数和loglog函数

二维图像

1.bar函数

2.histogram函数

3. polarhistogram函数

4.pie函数

 5.stairs函数

6.stem函数

7.fill函数

8.scatter函数

9.area函数

10.compass函数、feather函数和quiver函数

三维曲线

1.plot3函数

 2.fplot3函数

三维图像

1.mesh函数

 2.surf函数

3.fmesh函数和fsurf函数

 4.sphere函数

 5.cylinder函数

6.peaks函数

 7.fimplicit3函数

 8.bar3和bar3h函数

 9.stem3函数

 10.pie3函数

 11.fill3函数

 12.contour3函数

 13.waterfall函数

曲线样式设置

1.曲线基本属性

2.多图形显示

3.图像叠加

二维曲线

1. plot函数

plot函数在MATLAB中最广泛使用的绘图函数。

plot函数以下这些基本调用格式：

1. 
2. 
3. 

（1）、当plot函数只有一个输入参数时

当y是实型的参数时，表示以该元素的下标为横坐标，该元素的值为纵坐标绘制一条曲线；如果y是一个复型向量，则以向量的实部和虚部绘制一条曲线；若y是一条实型矩阵，则按列绘制每一列元素值相对其下标的曲线，曲线的条数等于输入参数矩阵的列数；若y是复型的矩阵，则以实部为横坐标、虚部为纵坐标绘制曲线。

当y是实型向量时，例如：

clear;
clc;
y=[1,5]
plot(y)
xlabel('x')
ylabel('y')

效果图如下所示：

实型向量效果图

 当y是复型向量时，例如：

clear;
clc;
y=[3+4i,5+6i]
plot(y)
xlabel('实部')
ylabel('虚部')

效果图如下所示：

复型向量效果图

 当y是实矩阵时，例如绘制一个同心圆：

clc;
clear;
z=linspace(0,2*pi,100);
x=cos(z)+1i.*sin(z);
y=[x;2*x;3*x]';
plot(y)

效果图如下所示：

 当y时复型矩阵的时，例如：

clc;
clear;
y=[1+2i,3+7i,4+5i;7+8i,2+10i,9+3i];
plot(y)

效果图如下所示：

 （2）、当plot函数有两个输入参数时

plot(x,y)函数的作用是以x为自变量、y为因变量绘制带节点标记的线条或者是以x、y为标记的坐标点。其中，x和y要求是同等长度的向量，分别用于存储数据点的横坐标以及纵坐标。

例如，绘制y=sin x在[0,2Π]区间内的图像，代码如下所示：

clc;
clear;
x=0:pi/100:2*pi;
y=sin(x);
plot(x,y)
xlabel('x')
ylabel('y')

效果图如下所示：

sin x图像

 再例如，绘制如下公式的曲线得：

                                                           

代码段如下所示：

clc;
clear;
t=linspace(0,2*pi,100);
x=2*cos(t)+sin(15*t);
y=2*cos(t)-sin(15*t);
plot(x,y)

效果图如下所示：

（3）当plot函数有三个及以上的输入参数的时

当plot函数有多个输入参数时，公式如下所示：

                                                        

 在上式中，和组成一组向量对、和组成了一组向量对、和组成了一组向量对...和组成一组向量对，以每一组向量对的横纵坐标绘制出一条曲线。

例如，在同一坐标系下同时绘制出正弦和余弦曲线，代码为：

clc;
clear;
x=0:pi/100:2*pi;
y1=sin(x);
y2=cos(x);
plot(x,y1,x,y2)
xlabel('x')
ylabel('y')

效果图如下所示：

 2.fplot函数

从R2014b版本开始，MATLAB开始提供fplot函数，可以根据参数的变换来自适应调整采样间的间距；从R2016a版本开始，MATLAB提供了输入参数的用法。使用fplot函数的好处是当因变量的值变量缓慢时，设置采样的间距大；当因变量的值变换较快的时，设置采样的间距较小。简单来说，fplot函数绘制图像是自适应的，在绘图的时候我们不需要考虑具体要绘制哪些点的值。

例如我们已下面这个公式来分别比较plot函数和fplot函数之间的区别：

                                                                         

若使用plot函数绘制图形代码如下所示：

clc;
clear;
x=-2*pi:pi/100:2*pi;
y=x.^2.*sin(1./x);
plot(x,y)

效果图如下所示：

plot函数绘制效果图

使用fplot函数的代码部分如下图所示：

fplot(@(x) x.^2.*sin(1./x),[-1,1])

 如下图所示：

fplot函数绘制效果图

通过对于两张图形之间的比较可以得出，在这种情况下，使用fplot函数的效果更好，而使用plot函数来绘制图像的效果就比较差。

相对于plot函数采用等间距采样，fplot能够适应一些特殊情况下的函数，其调用的格式如下所示：

                                                         

其中funx、funy代表函数，lims代表函数的取值范围。

3.fimplicit函数

给出函数的显示表达式，用户可以使用plot函数和fplot函数来绘制图像，但是如果是隐式表达式那么上述函数就不能绘制出来，从R2016b开始，MATLAB开始提供fimplicit函数绘制隐函数的图形，该函数的调用格式如下所示：

                                                               

f是匿名表达式或者是函数句柄，[a,b]指定x轴的取值范围，[c,d]指定y轴的范围，如果没有指定范围就默认范围为[-5,5]。

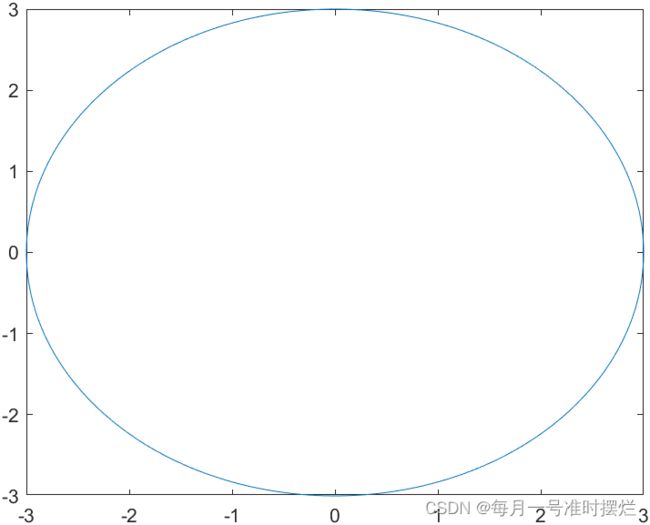
例如使用fimplicit函数来绘制以原点为圆心，3为半径的圆形，代码如下所示：

fimplicit(@(x,y)x.*x+y.*y-9)

效果图如下所示：

 在例如绘制下面数学表达式的函数公式的图像可得：

                                                                                           

代码如下所示：

fimplicit(@(x,y)x.*y+exp(y)-x-1)

效果图如下所示：

 4.polarplot函数

极坐标轴图以从同一点开始的轴上表示的三个或更多个定量变量的二维图表的形式显示多变量数据的图形方法。它可以将多维数据进行表示，但是点的相对位置和坐标轴之间的夹角是没有任何信息的。MATLAB中使用polarplot函数来绘制极坐标图，其调用的格式如下所示：

                                                          

上述式子中，theta为极坐标角，rho为极坐标极径，option表示的是选项。

例如，利用polarplot函数来绘制一个心形图，公式如下所示：

                                                                

代码如下所示：

t=0:pi/40:2*pi;
r=2*(1+cos(t));
polarplot(t,r)

效果图如下所示：

 我们同样可以使用MATLAB来绘制其他的图案，例如使用MATLAB来绘制蝴蝶曲线，公式如下所示：

                                                         

代码如下所示：

a=0:pi/50:20*pi;
r=exp(cos(a-pi/2))-2*cos(4*(a-pi/2))+sin((a-pi/2)/12).^5
polarplot(t,r)

效果图如下所示：

 5.contour函数和contourf函数

等高线图是在地图上表示起伏的常用方法，它是采用等高线所组成的平面图形来表示地面的高低起伏，等高线图在地理中被广泛应用。等高线是地面上高程相等的各相邻点所连成的闭合曲线。MATLAB提供了contour函数和contourf函数来绘制等高线。这两种函数的用法如下所示：

                                                     

                                                     

上式中，x和y分别表示横坐标和纵坐标，z表示高程。当x和y是矩阵的时候，大小应该与z相同；选项n是标量，指定用n来条水平线来绘制等高线；v是单调递增向量，其中的每一个元素对应着一条水品线的值，v中元素的个数代表中等高线的个数。n和v的值可以省略，如果数量和水平线的值将根据z的最大值和最小值来确定。

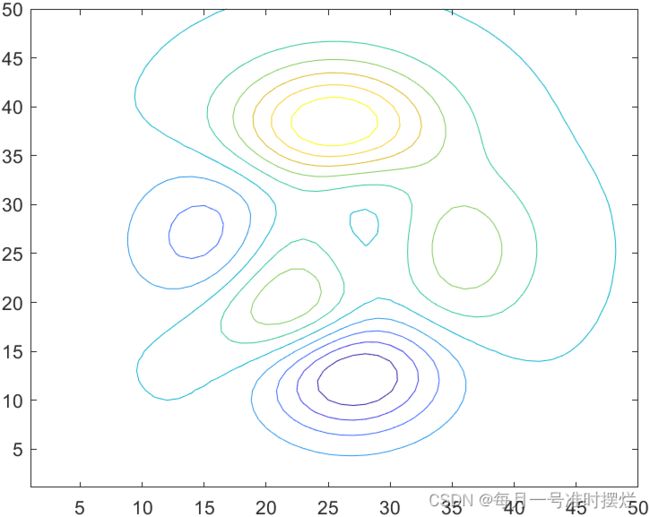
contour函数用于绘制常规的等高线，contourf函数用于绘制填充方式的等高线图。

contour(peaks(50),10)

效果图如下所示：

6.semilogx函数、semilogy函数和loglog函数

在工程实际问题中，通过对于数据进行转换可以清晰地看出数据的某一些特征，通过对数坐标反映信号幅频特征和相频特征。MATLAB中提供了以下这些函数：

                                        

                                        

                                           

在上面的式子中，x和y分别表示的是横纵坐标，option表示的是选项。semilogx函数表示的是x轴为常用对数刻度，y轴是线型刻度。semilogy函数表示的是y轴使用对数刻度，而x轴使用的线型刻度。loglog是全对数坐标，x轴和y轴均是采用对数刻度。

例如下面利用semilogy函数将y=exp(x)用直线的方式表示出来：

x=0:0.1:10;
y=exp(x);
semilogy(x,y)

效果图如下所示：

二维图像

二维图形是指不好含深度信息的平面图象，只有左右、上下四个方向，不存在前后。在一个平面上的图形即可以看成是二维图形。二维图形只有面积没有体积。

1.bar函数

条形类图形中用高度不等的条形来表示数据的大小，如下表所示为MATLAB中条形图和直方图的函数以及功能：

条形图和直方图的功能

函数	具体的功能
bar	绘制条形统计图
barh	绘制水平条形统计图
histogram	绘制直方图
pareto	绘制排序直方图
polarhistogram	极坐标直方图
Histcounts	直方图区间记数
histogram2	绘制二元直方图
histcounts2	二元直方图区间记数

bar函数的基本使用方法如下所示：

                                                            

在上式中，x表示存储绘图数据，则分别以每个元素的值来作为每一个矩阵条的高度，以对应元素的下标作为横坐标；如果x是一个m×n的矩阵，那么以bar函数创建m组包含n个条形；width设置条形的相对宽度以控制组中各个条形的间隔，将width设置为一个标量，默认的宽度为0.8；style用来表示条形图的类型，可以是grouped（簇状图）、stacked（堆积）、histc（横向直方图）、hist（纵向直方图），系统默认的是以簇状图的方式来进行排列。

例如，我们利用MATLAB代码绘制以下几位同学的学生成绩的直方图：

学生成绩表

姓名	语文	数学	英语
甲	95	92	89
乙	87	91	76
丙	79	93	92
丁	88	87	94

使用MATLAB程序将上述表格的内容绘制成直方图的代码如下所示：

x=[95,92,89;87,91,76;79,93,92;88,87,94]
subplot(2,1,1)
bar(x,'stack');
subplot(2,1,2)
barh(x,'Group')

则两张效果图的图片如下面两张图片所示：

竖型堆积型效果图

水平簇状型效果图

2.histogram函数

直方图是一种统计报告图，由一系列高度不等的纵向条纹或者线段表示数据的分布情况。一般横向表示数据类型，纵轴表示分布情况。MATLAB中提供了绘制直方图的histogram函数。histogram函数的基本调用格式如下所示：

                                                                

上式中，输入参数x表示的是存储绘图数据，而nbins用于统计区间的划分情况，若nbins是一个正整数的话，则统计区间分均分为nbins个小区间；如果nbins是向量，则向量中的每一个元素指定各个区间的最小值，默认以x中的值来划分区间。

例如：

x=[4,3,2,6,5,4,2,8];
h=histogram(x)

结果显示为：

3. polarhistogram函数

在极坐标系，MATLAB同样提供了直方图函数。MATLAB提供了ploarhistogram函数绘制极坐标直方图，其格式如下所示：

                                                          

参数thera是一个向量，用于确定每一个区间与原点的角度。绘图时将圆划分成了若干个角度相同的扇形区域，每一个扇形区域反映落入该区间的个数。nbins是一个标量，则表示[0,2Π]区间划分成了多少个扇形区域；如果nbins为向量，则表示分组的值，一般默认为20。

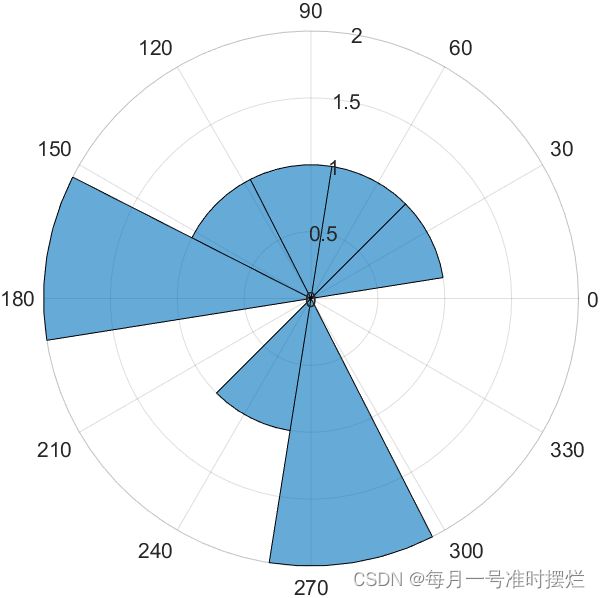
例如如下的示例：

theta=[1.1,4.2,3,5,7,8,5,3,2.4];
polarhistogram(theta,10)

上述代码运行的效果图如下所示：

极坐标直方图

4.pie函数

饼状图，又称为扇形统计图，可以反映一个数据在所有项中所占比例，MATLAB中提供pie函数绘制饼状图。pie函数的基本调用格式如下所示：

                                                                     

上述公式中，输入参数为存储绘图数据。选项explode是与x同等大小的向量或者矩阵，与explode的非零值对应的部分从饼图中分离出来。explode省略时，饼图是一个整体。

例如统计某位学生在四次考试过程中各科成绩占总分的比例，代码如下：

x=[78,68,83,91;87,85,89,91;92,93,90,78;94,93,95,79]
pie(x(:,1))
legend('语文','数学','英语','物理')

效果图如下所示：

 5.stairs函数

阶梯图常用于x的值发生了突然的变化之后，y值因此发生了离散的变化，是一种使用标准阶梯符号的语言。MATLAB中使用stirs函数来绘制阶梯图。

例如，绘制[0,4Π]区间内y=sin x的阶梯图，代码部分如下所示：

x=linspace(0,4*pi,50);
y=sin(x);
stairs(y)

效果图如下所示：

6.stem函数

火柴杆图又称为是棒棒糖图，核心元素是一个柱子再加上一个圆圈，属于柱状图的一种变体。MATLAB中使用stem函数来绘制火柴杆图。

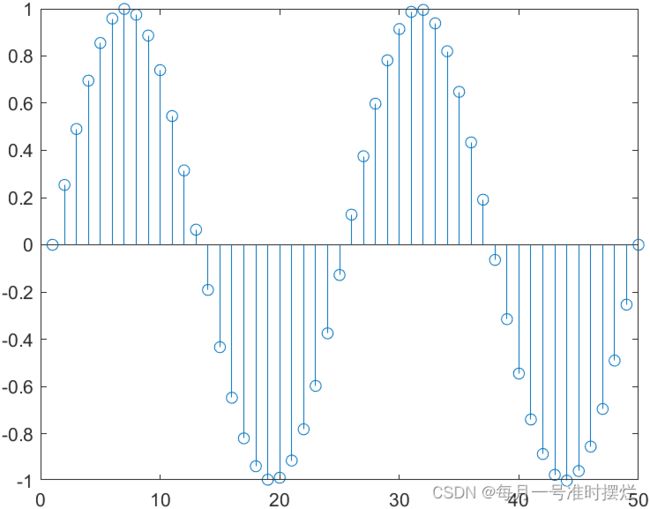
例如，绘制[0,4Π]区间内y=sin x的火柴杆图，代码部分如下所示：

x=linspace(0,4*pi,50);
y=sin(x);
stem(y)

效果图如下所示：

7.fill函数

实心图是将数据的起点和终点连接成多边形，并填充颜色。MATLAB提供了fill函数来绘制实行图，fill函数的调用格式如下所示：

                                          

上式中option表示的意思为选项，fill函数按向量元素下标依次用直线连接x、y所对应的数据点。若连接的折线不是封闭的，那么MATLAB就会将所有元素连接起来，形成封闭的多边形。

例如，利用正弦函数和余弦函数绘制一个八边形的实心图，代码部分如下所示：

clc;
clear;
a=0:pi/4:2*pi;
x=sin(a);
y=cos(a);
fill(x,y,'r')

效果图如下所示：

8.scatter函数

平面散点图可以描述离散数据的分布变化的情况，MATLAB中利用scatter函数来绘制平面散点图，其基本调用格式如下所示：

                                                     

其中，x、y、sz和c表示同等大小的向量。x、y分别表示横纵坐标向量，它们的长度必须是相同的。s是一个和x、y等长的向量，用来指定各个数据点的大小，也可以是一个标量；如果s是一个标量，那么与所有数据点同等大小。c代表的是颜色，c与s一样，可以是一个与x、y等长的一个限量，也可以是以RGB三元组。要想使用不同的颜色，可以将c指定为向量或是有RGB三元组组成的三元矩阵。

例如，如下表所示为1980年-2010年北京市12个月的平均气温，将下面的数据用散点图来表示出来。

北京市1980年-2010年每月平均气温

月份	1	2	3	4	5	6	7	8	9	10	11	12
温度（单位：°C）	-3	0	8	15	22	26	28	27	21	14	5	-1

程序代码如下所示：

month=[1,2,3,4,5,6,7,8,9,10,11,12];
t=[-3,0,8,15,22,26,28,27,21,14,5,-1];
scatter(month,t,50)

上述程序的效果如下所示：

9.area函数

面积图又称作为区域图，用于描述数量随时间变化或是类似变化的趋势。MATLAB中使用area函数来绘制面积图。area函数的基本调用格式如下所示：

                                                           

输入参数y是一个向量，也可以是一个矩阵。如果y是一个向量，那么就以y为纵坐标绘制一条曲线，填充曲线内的区域。如果y是一个矩阵，那么y的每一列元素都对应一条曲线，堆叠起来绘制多条曲线，每一条曲线由不同的颜色填充。而basevalue表示指定区域的基本值。

x=[4,3,5;7,6,9;7,8,9;10,13,12]
area(x)

上述代码运行的效果图如下所示：

10.compass函数、feather函数和quiver函数

矢量的定义是既有大小又有方向的向量，在数学、物理以及工程中有着广泛的应用，通常使用有方向的箭头来表示矢量。MATLAB中提供了多个函数来表示矢量图，具体如下所示。

1. 使用compass函数来表示用原点发出的矢量图。
2. 使用feather函数用从x轴发射出的箭头的矢量图。
3. 使用quiver函数来表示从平面中指定的位置发射出的矢量图。

上述几种函数的调用的格式如下所示：

                                            

                                             

                                                             

                                                         

在上面的公式中，z表示的复型量，x、y、u、v和w都表示的是同型矩阵，以(x,y)为起点，u,v都是x,y方向的速度分量。

下面代码为使用compass函数代码的示例：

u=[2,4,-5;6,-7,8];
v=[6,-7,4;7,-9,-12];
compass(u,v)

上述示例的图如下所示：

下面代码为使用feather函数的示例：

a=[1+2i;-3+2i;5-3i];
feather(a)

上述代码的效果图如下所示：

 下面代码为使用quiver函数的示例：

z=[3+2i,2+4i,5-7i,6+9i];
quiver([3,4,0,-1],[-2,4,6,4],real(z),imag(z))

上述示例的效果图如下所示：

三维曲线

与现实世界不同，计算机中的三维图形是通过平面展示出来的， 是利用的是在计算机屏幕上的色彩灰度的不同而使人产生的错觉。MATLAB中提供了较多的函数来绘制三维图形，MATLAB用来绘制三维图形的方法与绘制二维图形的方法相似。

1.plot3函数

同二维平面中plot函数相同，plot3函数同样也是在三维平面中使用最多的一个函数之一，使用方法与plot函数相似。调用方法如下所示：

                                                           

上式中x、y和z的值是可以是一组向量或者是矩阵。当x、y和z是向量的时候，x、y和z构成了一条曲线上各个数据点的空间坐标；当x、y和z是同样大小的矩阵的时候，曲线的条数和矩阵的列数是相同的；当x、y和z中既有向量又有矩阵的时候，行向量的长度与矩阵的列数相同，列向量的长度与矩阵的行数相同。

例如，绘制如下公示的三维的三维图形：

                                                                 

上述公式中c为常数。

代码段，如下所示：

r=2;
c=4;
a=0:pi/60:20*pi;
x=r*cos(a);
y=r*sin(a);
z=c*a;
plot3(x,y,z)

效果图如下所示：

 2.fplot3函数

与fplot函数的原理相似，fplot函数是为了在三维图形中能够更好反映图像的真实性，因为如何使用plot3函数所使用间隔是同等的，在一些情况很难反映出真实情况，所以MATLAB从R2016开始提供了fplot3函数，可以根据参数函数的变化特征来自适应设置采样间隔。如果变化缓慢的话，就设置间隔较大一些，如果变化较大的话，设置采样的间隔较小。fplot的调用格式如下所示：

                                                    

上述公式中，funx、funy和funz分别表示x、y和z的坐标，lims表示的是自变量的取值范围，用二元向量[tmin,tmax]描述，默认为[-5,5]。

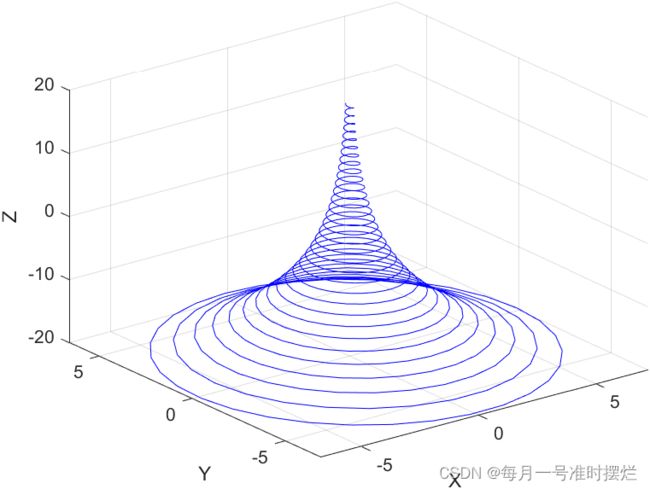
例如，绘制墨西哥帽顶曲线，曲线的参数方程如下所示：

                                                              
代码部分如下所示：

x = @(t)exp(-t/10).*sin(5*t);
y = @(t)exp(-t/10).*cos(5*t);
z = @(t)t;
fplot3(x,y,z,[-20,20],'b')
xlabel('X')
ylabel('Y')
zlabel('Z')

效果图如下所示：

 如果我们使用plot函数来绘制该图形，代码段如下所示：

t=-20:0.2:20
x = exp(-t/10).*sin(5*t);
y = exp(-t/10).*cos(5*t);
z = t;
plot3(x,y,z,'b')
xlabel('X')
ylabel('Y')
zlabel('Z')

效果图如下所示：

 通过对于上面两张效果图进行对比，不难发现，fplot3更加使用对于这种情况下的绘制情况更好，更加适合墨西哥帽顶曲线。

三维图像

1.mesh函数

MATLAB提供了mesh函数和surf函数来绘制三维图像。mesh函数用于绘制三维网格图，线条带有颜色。mesh函数的调用格式如下所示：

                                                            

上述函数中，x、y的值表示xoy平面的坐标，z的值表示该点的高度。通常输入参数x、y和z是同型矩阵，特殊情况下，x的长度表示矩阵z的列数，y的值表示矩阵的行数。

例如，绘制一下公式的曲线：

                                                            

代码部分如下所示：

clc;
clear;
x=linspace(-3*pi,3*pi,45);
y=linspace(0,3*pi,45);
[X,Y]=meshgrid(x,y);
Z=X.*sin(Y).*exp(-sqrt(X.^2+Y.^2)/2);
mesh(X,Y,Z)

效果图如下所示：

 2.surf函数

surf函数与mesh函数相似，区别就是mesh函数的网格线条之间是无颜色的，而surf函数的网格线之间是有颜色的，surf函数的公式如下所示：

                                                           

代码部分如下所示：

x=linspace(-3*pi,3*pi,45);
y=linspace(0,3*pi,45);
[X,Y]=meshgrid(x,y);
Z=X.*sin(Y).*exp(-sqrt(X.^2+Y.^2)/2);
surf(X,Y,Z)

效果图如下所示：

3.fmesh函数和fsurf函数

mesh函数和surf函数在一些情况由于间距设置不够大，可能会造成不能反映真实特性的情况。和fplot函数和fplot3函数相同，从R2016a开始，MATLAB提供了fmesh和fsurf函数可以根据函数的变化特性来自适应设置网格顶点之间的间距。fmesh函数和fsurf函数的调用格式如下所示：

                                                         
                                                         

                                           

                                           

上述四个式子中，funx、funy和funz分别表示网格中的顶点x、y和z的坐标的函数，fun表示一个二元函数的输入参数。funx、funy和funz都有两个自变量，lims表示自变量的取值范围，用四元向量[umax,umin,vmax,vmin]来描述，umax、umin表示自变量上下界，vmin、vmax表示因变量上下界。option表示的意思是选项。

例如，利用MATLAB的fsurf函数来绘制墨西哥帽顶图，代码部分如下所示：

fsurf(@(x,y)sin((x.^2)+(y.^2))./((x.^2)+(y.^2)),[-4,4,-4,4])

效果图如下所示：

 4.sphere函数

MATLAB中提供了用于绘制标准的三维曲面，其中MATLAB提供了生成三维球面数据的sphere函数。调用格式如所示：

                                                                 

该函数将产生3（n+1）函数：[x,y,z]个方阵，通过这个三个矩阵可以绘制出圆心在原点，半径为1的单位球体。例如，当[x,y,z]=sphere(3)所产生的矩阵如下所示：

x =

         0         0         0         0
   -0.8660    0.4330    0.4330   -0.8660
   -0.8660    0.4330    0.4330   -0.8660
         0         0         0         0

y =

         0         0         0         0
         0   -0.7500    0.7500         0
         0   -0.7500    0.7500         0
         0         0         0         0

z =

   -1.0000   -1.0000   -1.0000   -1.0000
   -0.5000   -0.5000   -0.5000   -0.5000
    0.5000    0.5000    0.5000    0.5000
    1.0000    1.0000    1.0000    1.0000

或者直接使用sphere函数绘制原点是(0,0,0)，半径为1的球面，代码如下：

sphere

效果图如下所示：

 5.cylinder函数

cylinder函数用于绘制柱面，其调用格式如下所示：

                                                                

上述公式中，r表示的各个相等间隔高度上默认点之间的距离，n表示圆柱体上有几个默认点，在默认情况下，r的默认值为1，n的默认值为1，默认有20个间隔点。

例如，绘制半径为5，高度为1的圆柱体的代码如下所示：

cylinder(5)

效果图如下所示：

cylinder函数不仅可以用来绘制圆柱体，而且可以用来绘制圆锥体，例如下面的代码：

cylinder(0:0.02:2);

效果图如下所示：

再例如要绘制侧面轮廓为2+cos a的圆柱面，代码如下所示：

a=0:pi/20:2*pi;
[x,y,z]=cylinder(2+cos(a))
mesh(x,y,z)

效果图如下所示：

6.peaks函数

peaks函数用于生成网格顶点的高度矩阵.基本调用格式如下所示：

                                                              

                                                           

                                                         

上述公式中，第一个公式中的n值为标量时候，是将[-3,3]分为n-1份，默认为49份。第二个公式中的k为一个向量，生成一个方阵。第三个公式中的u和v是大小相同的矩阵，生成的是与u、v大小相同的矩阵。

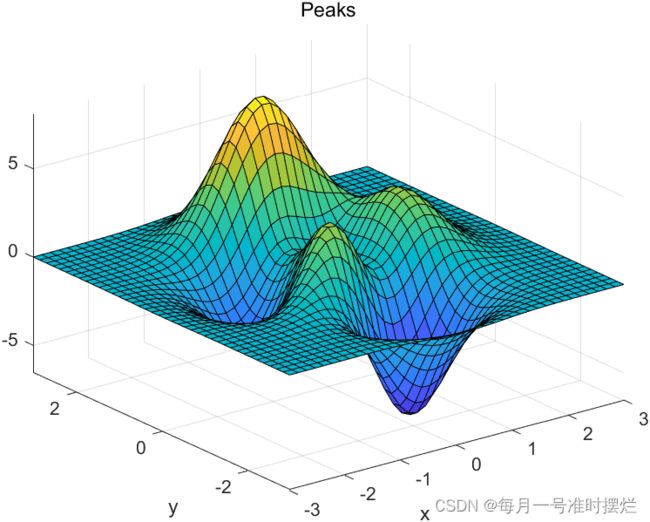
例如：

peaks(40)

效果图如下所示：

再例如下面代码所示：

x=linspace(0,2,100);
peaks(x)

 效果图如下所示：

 7.fimplicit3函数

同fimplicit函数相同，从R2016a开始，MATLAB开始提供fimplicit3函数来对于隐函数进行绘制，调用的格式如下所示：

                                                             

其中，f是匿名表达式的函数句柄，[a b]、[c d]和[e f]分别表示函数的取值范围，如果省略取值范围则默认为[-5,5]。

例如，绘制如下表达式的在[-2,2]之间的三维图像。

                                                   

代码部分如下所示：

fimplicit3(@(x,y,z)x.^2+y.^2+z.^2-2,[-2,2])

效果图如下所示：

 8.bar3和bar3h函数

MATLAB中使用bar3和bar3h函数来绘制水平的和垂直的三维图形图，调用格式如下所示：

                                                                 

                                                                 

其中，x是向量，y是向量和矩阵。如果y是m×n的矩阵的话，那么x向量元素的个数与y的行数相同，即x的变化范围为1到n。如果x的值省略，y是长度为a的向量，那么x的变化范围是1到n；

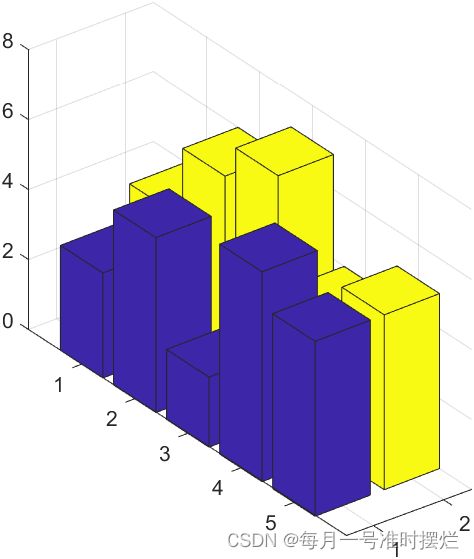
a=[3,4;5,6;2,7;6,4;5,5]
bar3(a)

效果图如下所示：

 9.stem3函数

在MATLAB中提供了stem3函数来绘制三维直方图，调用格式如下所示：

                                                                       

                                                                  

x、y和z表示在xoy平面上指定的位置上绘制z的直方图。例如：

x=linspace(-2,2,40);
stem3(x)

效果图如下所示：

 10.pie3函数

MATLAB中提供了pie3函数来绘制三维饼图，其调用格式如如下所示：

                                                              

上述公式中，x为向量。例如绘制一个三维饼图的代码如下所示：

x=[1,3,4,5,6,7,8.4];
pie3(x)

效果图如下所示：

 11.fill3函数

MATLAB提供了fill3函数来绘制填充的多边形图，调用格式如下所示：

                                                   

上式中，x、y和z分别表示多边形的顶点，而c表示填充多边形的颜色。例如如下代码：

x=[4;5;5];
y=[7;8;9];
z=[6;5;6];
fill3(x,y,z,'b');

效果图如下所示：

 12.contour3函数

MATLAB提供了contour3函数来绘制三维等高线图，其调用格式如下所示：

                                                                   

其中，x、y和z分别表示相同行数和列数的向量，k表示为高度的等级度，c表示为曲线的颜色。代码如下所示：

[X,Y,Z]=peaks(60);
contour3(X,Y,Z,8,'b')

效果图如下所示：

 13.waterfall函数

MATLAB提供了waterfall函数来绘制瀑布图，瀑布图是一种等高线图，瀑布图的基本调用格式如下所示：

                                                        
上式中，x、y和z分别表示的是行数和列数相等的向量。例如：

[X,Y,Z]=peaks(60);
waterfall(X,Y,Z)

效果图如下所示：

曲线样式设置

1.曲线基本属性

在使用MATLAB绘制图形的时候，常常在加上图像所具有的属性为图像增添特色，比如：颜色、线性、数据点的特殊标记等。

如下表所示为列表的颜色属性选项：

曲线颜色选项

选项	颜色
r或者red	红色
y或者yellow	黄色
g或者green	绿色
c或者cyan	青色
b或者blue	蓝色
k或者black	黑色
m或者magenta	品红色

除了上述直接标注颜色的方式还可以使用RGB三元组来表示颜色，[R G B]指定颜色，R、G、B分别代表的是红色、蓝色和绿色三种颜色的亮度，取值的范围是[0,1]。例如，下表为常见颜色的RGB表：

RGB值	颜色
[1 1 1]	白色
[0 0 0]	黑色
[0 0 1]	蓝色
[0 1 0]	绿色
[1 0 0]	红色
[1 1 0]	黄色
[1 0 1]	品红色
[0 1 1]	青色

除了颜色这个属性之外，还有曲线的线型选项。如下表所示线型选项：

曲线线型选项

线型	说明
-	实线
--	虚线
:	点线
-.	点划线
'o'	圆圈
'+'	加号
’.‘	点
’ב	叉号
'^'	上三角
’v‘	下三角
’<‘	左三角
’>‘	右三角
’|‘	垂直线条
’s‘	方形
’d‘	菱形
'p'	五角星
’h‘	六角形
’*‘	星号

MATLAB的绘图中所有的属性如下所示：

• LineWidth：指定线宽，默认为0.5像素。
• LineMarker：指定线型。
• Color：颜色，参考上表所示。
• Marker：指定标记的符号。
• MarkerIndices：指定哪些是显示标记，其值为向量。默认情况下在每一个数据点标记。
• MarkEdgeColor：使用特定的颜色绘制特有的形状的标记图形，特定的图形包括五角星、菱形、六角形。颜色包括上述表格中的颜色和所有RGB颜色。
• MarkerFaceColor：使用特定的颜色来填充特定形状的图形，特定的图形包括五角星、菱形、六角形。颜色包括上述表格中的颜色和所有RGB颜色。
• MarkerSize：标记符号大小，默认6像素。

2.多图形显示

MATLAB可以多个图形窗口显示，可以将一个窗口分割为多个绘图区，多个图像由多个绘图区显示，每一个绘图区域都有自己特定的坐标，每一个绘图区称为子图，MATLAB提供了subplot函数对于当前内容进行分割，基本格式如下所示：

                                                                         

其中，m和n分别表示的是m行n列的绘图区，a是指的是当前绘图区，例如下面的例子：

x=0:0.1:2*pi;
y1=sin(x);
y2=cos(x);
y3=sin(x+pi/2);
subplot(2,2,1);
plot(y1);
subplot(2,2,2);
plot(y2);
subplot(2,2,3);
plot(y3);
subplot(2,2,4);
hold on;
plot(y1);
plot(y2);

效果图如下所示：

 上面例子中是将分割了四张子图来显示不同三角函数，这样可以更加简单区分曲线。

3.图像叠加

除了将图像进行分割以外，还可以将两个图像进行叠加，如果希望在已经存在的图形上面再添加图形，可以使用图像保持命令hold，hold on是保持原有图形，hold off是刷新原有图形。例如：

x=0:pi/20:2*pi;
y1=sin(x);
plot(x,y1);
hold on;
y2=cos(x);
plot(x,y2);

效果如下所示：